

| home |
| group members |
| publications |
| talks/presentations |
| teaching |
| Google Scholar Citations |
publications
- Nature of the Topological Transition of the Kitaev Model in [111] Magnetic Field,
S. Thiagarajan, C. Watson, T. Yzeiri, H. Hu, B. Uchoa, and F. Krüger,
Submitted to Phys. Rev. B, arXiv:2509.13057.
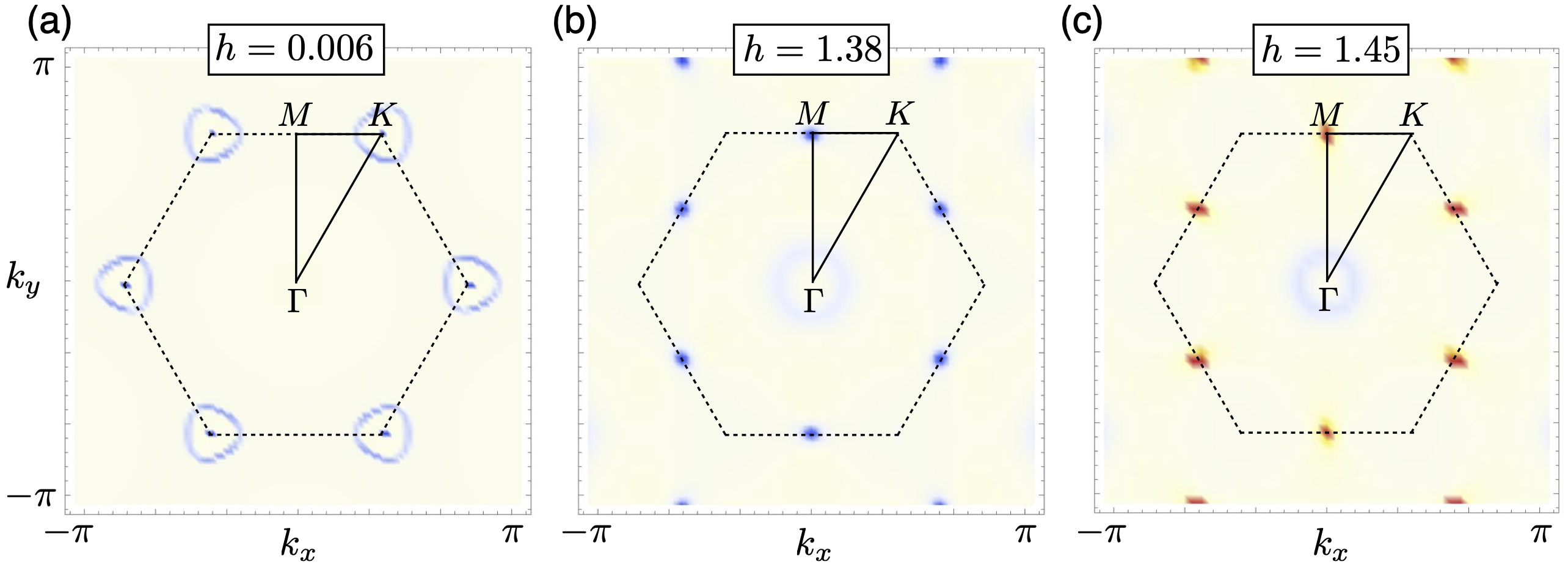
We investigate the nature of the topological phase transition of the antiferromagnetic Kitaev model on the honeycomb lattice in the
presence of a magnetic field along the [111] direction. The field opens a topological gap in the Majorana fermion spectrum and leads
to a sequence of topological phase transitions before the field polarised state is reached. At mean field level the gap first closes at
the three $M$ points in the Brillouin zone, where the Majorana fermions form Dirac cones, resulting in a change of Chern number by
three. An odd number of Dirac fermions in the infrared is unusual and requires Berry curvature compensation in the UV, which occurs
because of topological, ring-like hybridisation gaps with higher-energy bands. We perform a renormalisation-group analysis of the
topological phase transition at the three $M$ points within the Yukawa theory, allowing for intra- and inter-valley fluctuations of the
spin-liquid bond operators. We find that the latter lead to a breaking of Lorentz invariance and hence a different universality compared
to the standard Ising Gross-Neveu-Yukawa class.
- Quantum Criticality of Type-I and Critically Tilted Dirac Semimetals,
Huanzhi Hu and Frank Krüger,
Physica C 632, 1354687 (2025),
(Special edition on Quantum Matter dedicated to Jan Zaanen).
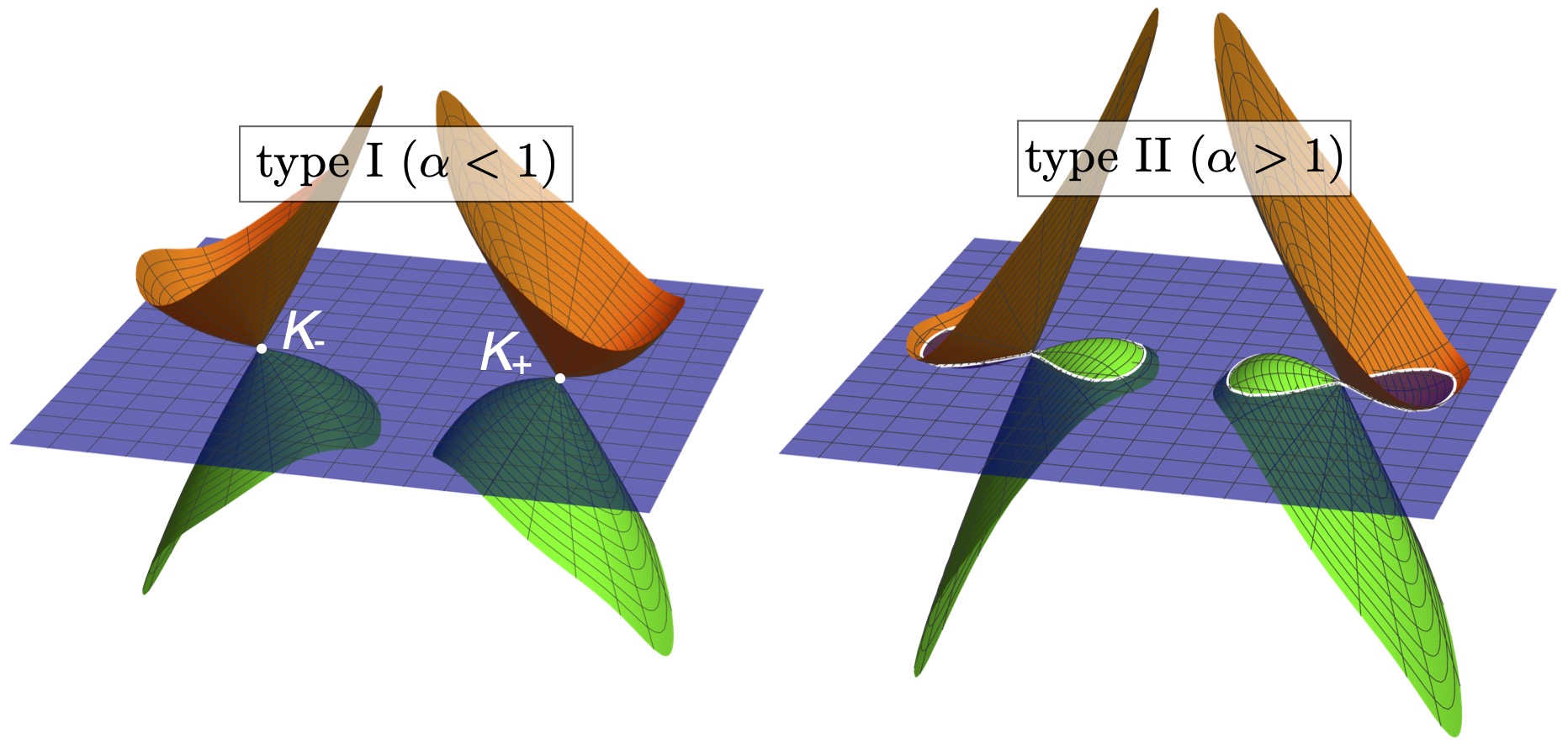
We investigate the universality of an Ising symmetry breaking phase transition of tilted two-dimensional Dirac fermions, in the
type-I phase as well as at the Lifshitz transition between a type-I and a type-II semimetal, where the Fermi surface changes from
point-like to one with electron and hole pockets that touch at the overtilted Dirac cones. We compute the Landau damping of
long-wavelength order parameter fluctuations by tilted Dirac fermions and use the resulting IR propagator as input for a
renormalisation-group analysis of the resulting Gross-Neveu-Yukawa field theory. We first demonstrate that the criticality of
tilted type-I fermions is controlled by a line of fixed points along which the poles of the renormalised Green function correspond
to an untilted Dirac spectrum with varying anisotropy of Fermi velocities. At the phase transition the Lorentz invariance is restored,
resulting in the same critical exponents as for conventional Dirac systems. The multicritical point is given by the endpoint of the
fixed-point line. It can be approached along any path in parameter space that avoids the fixed point line of the critical type-I
semimetal. We show that the critical exponents at the Lifshitz point are different and that Lorentz invariance is broken.
- Nature of Topological Phase Transition of Kitaev Quantum Spin Liquids,
Huanzhi Hu and Frank Krüger,
Phys. Rev. Lett. 133, 146603 (2024).
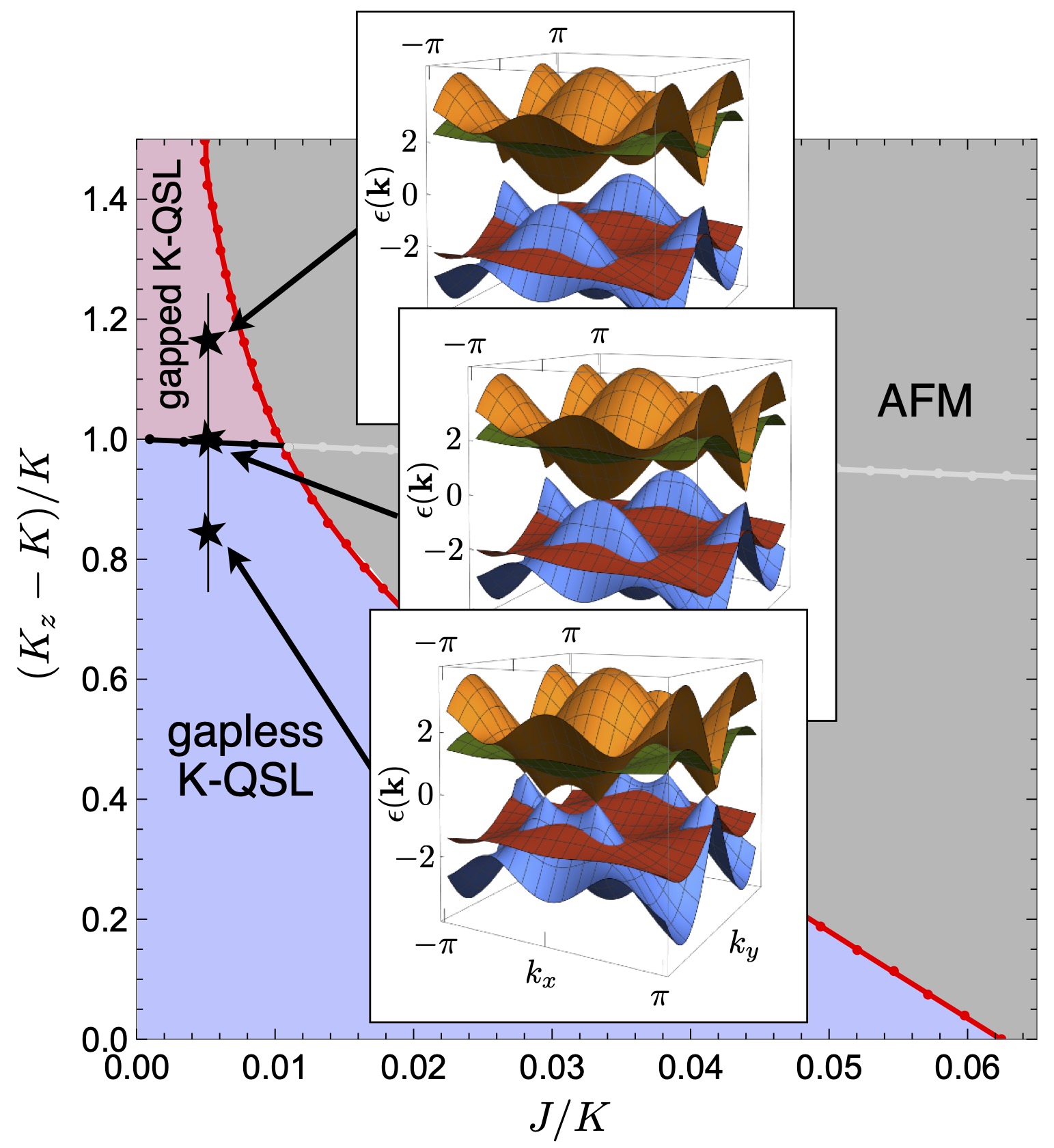
We investigate the nature of the topological quantum phase transition between the gapless and gapped Kitaev quantum spin liquid
phases away from the exactly solvable point. The transition is driven by anisotropy of the Kitaev couplings. At the critical point the two
Dirac points of the gapless Majorana modes merge, resulting in the formation of a semi-Dirac point with quadratic and linear band
touching directions. We derive an effective Gross-Neveu-Yukawa type field theory that describes the topological phase transition
in the presence of additional magnetic interactions. We obtain the infrared scaling form of the propagator of the dynamical Ising
order parameter field and perform a renormalization-group analysis. The universality of the transition is found to be different to that
of symmetry-breaking phase transitions of semi-Dirac electrons. However, as in the electronic case, the Majorana fermions acquire an
anomalous dimension, indicative of the breakdown of the fractionalized quasiparticle description.
- Majorana Fermion Mean-Field Theories of Kitaev Quantum Spin Liquids,
Shahnam Ghanbari Saheli, Jennifer Lin, Huanzhi Hu and Frank Krüger,
Phys. Rev. B 109, 014407 (2024).
We determine the phase diagrams of anisotropic Kitaev-Heisenberg models on the honeycomb lattice using parton mean-field theories
based on different Majorana fermion representations of the S=1/2 spin operators. Firstly, we use a two-dimensional Jordan-Wigner
transformation (JWT) involving a semi-infinite snake string operator. In order to ensure that the fermionized Hamiltonian remains local
we consider the limit of extreme Ising exchange anisotropy in the Heisenberg sector. Secondly, we use the conventional Kitaev
representation in terms of four Majorana fermions subject to local constraints, which we enforce through Lagrange multipliers. For both
representations we self-consistently decouple the interaction terms in the bond and magnetization channels and determine the phase
diagrams as a function of the anisotropy of the Kitaev couplings and the relative strength of the Ising exchange. While both mean-field
theories produce identical phase boundaries for the topological phase transition between the gapless and gapped Kitaev quantum spin
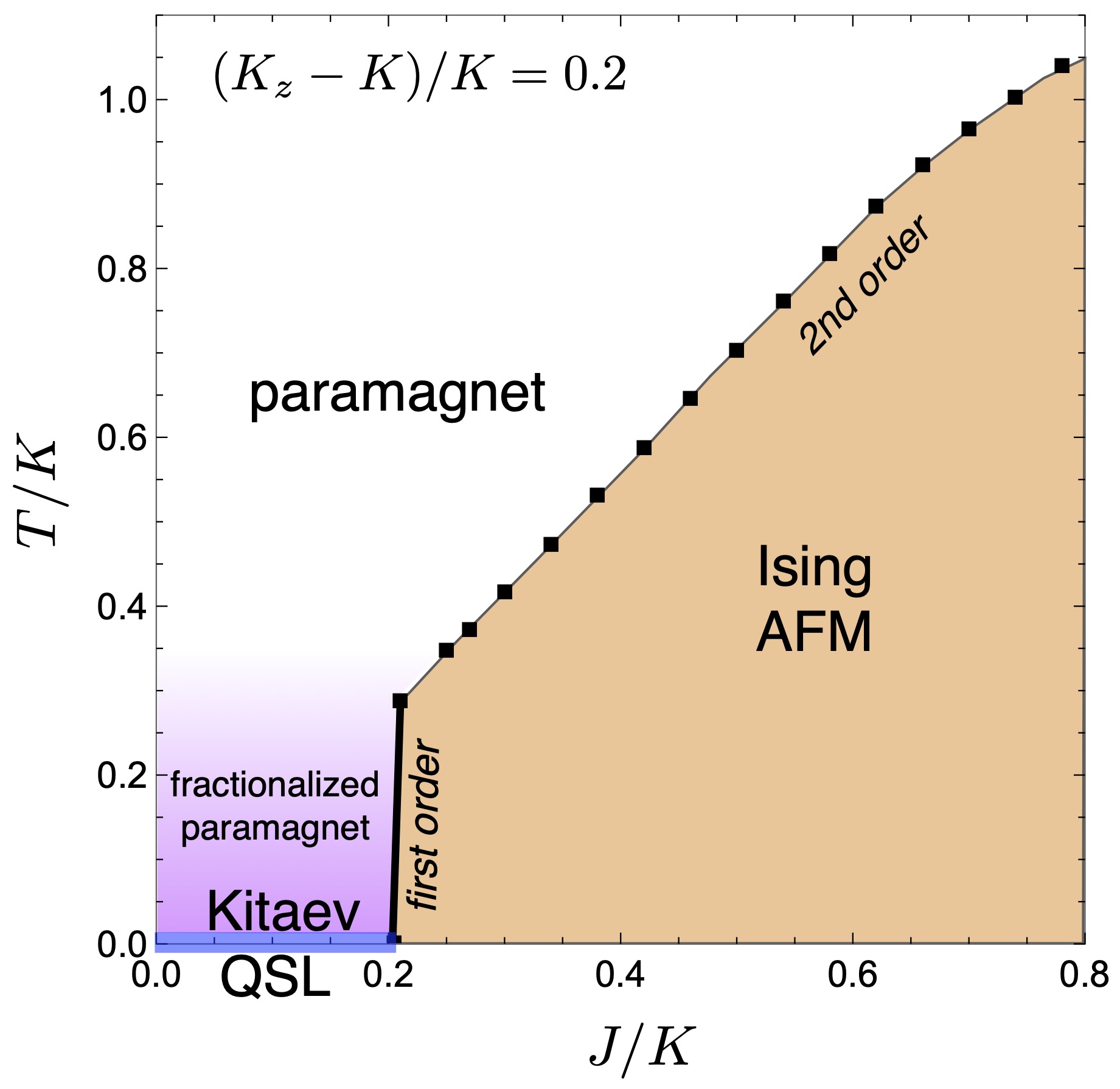
liquids, the JWT fails to correctly describe the the magnetic instability and finite-temperature behavior. Our results show that the
magnetic phase transition is first order at low temperatures but becomes continuous above a certain temperature. At this energy scale,
we also observe a finite-temperature crossover on the quantum-spin-liquid side, from a fractionalized paramagnet at low temperatures,
in which gapped flux excitations are frozen out, to a conventional paramagnet at high temperatures.
- Strain control of a bandwidth-driven spin reorientation in Ca3Ru2O7,
C.D. Dashwood, A.H. Walker, M.P. Kwasigroch, L.S.I. Veiga, Q. Faure, J.G. Vale, D.G. Porter, P. Manuel,
D.D. Khalyavin, F. Orlandi, C.V. Colin, O. Fabelo, F. Krüger, R.S. Perry, R.D. Johnson, A.G. Green, D.F. McMorrow,
Nature Communications 14, 6197 (2023).
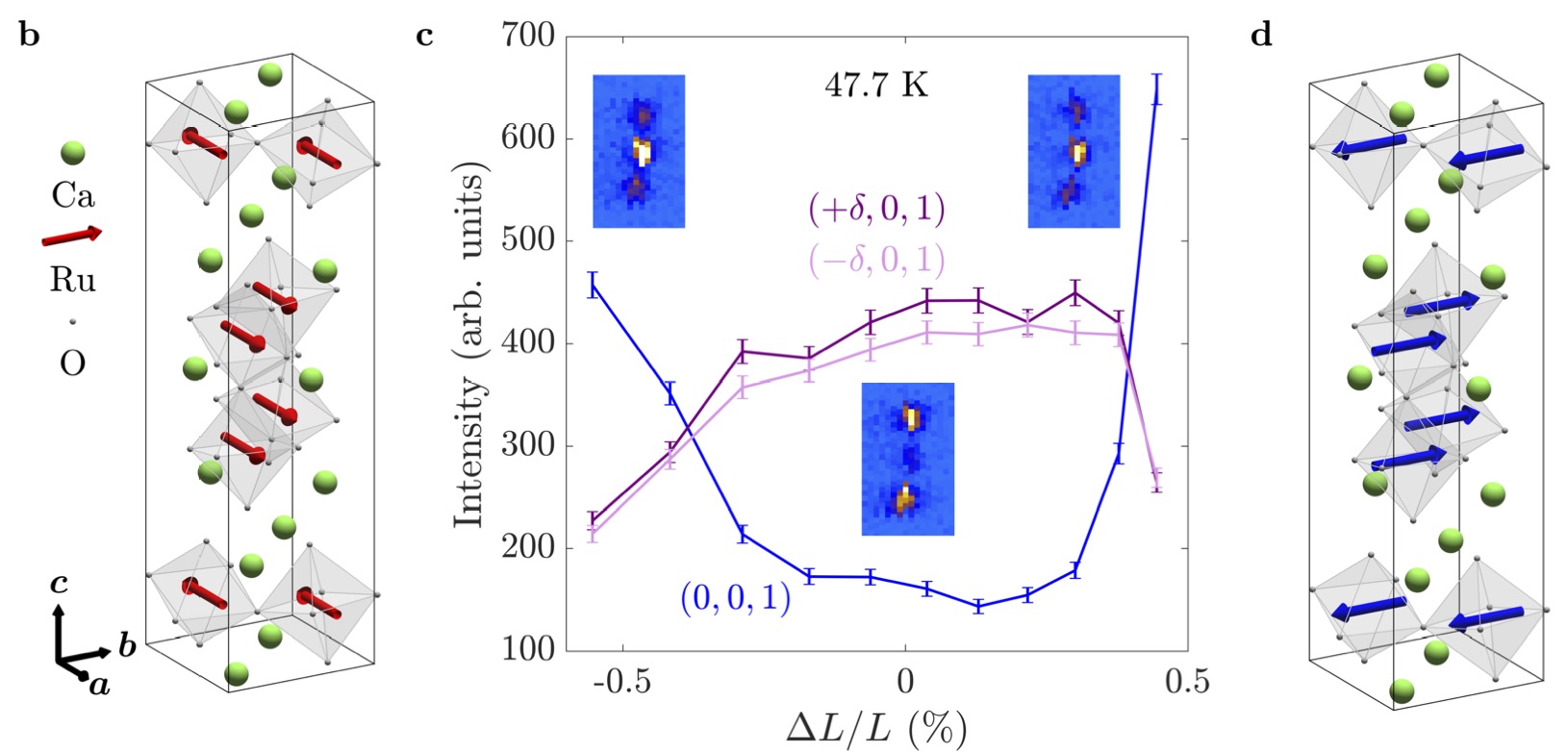
The layered ruthenate family of materials possess an intricate interplay of structural, electronic and magnetic degrees of freedom
that yields a plethora of delicately balanced ground states. This is exemplified by Ca3Ru2O7, which hosts a complex transition at
which the lattice parameters jump, the Fermi surface partially gaps and the spins undergo a 90deg in-plane reorientation. Here,
we show how the transition is driven by a lattice strain that tunes the electronic bandwidth. We apply uniaxial stress to single
crystals of Ca3Ru2O7, using neutron and resonant x-ray scattering to simultaneously probe the structural and magnetic responses.
These measurements demonstrate that the transition can be driven by externally induced strain, stimulating the development of a
theoretical model in which an internal strain is generated self-consistently to lower the electronic energy. We understand the strain
to act by modifying tilts and rotations of the RuO6 octahedra, which directly influences the nearest-neighbour hopping. Our results
offer a blueprint for uncovering the driving force behind coupled phase transitions, as well as a novel route to controlling them.
- Stability of the Néel quantum critical point in the presence of Dirac fermions,
Huanzhi Hu, Jennifer Lin, Mikolaj D. Uryszek, and Frank Krüger,
Phys. Rev. B 107, 085113 (2023).
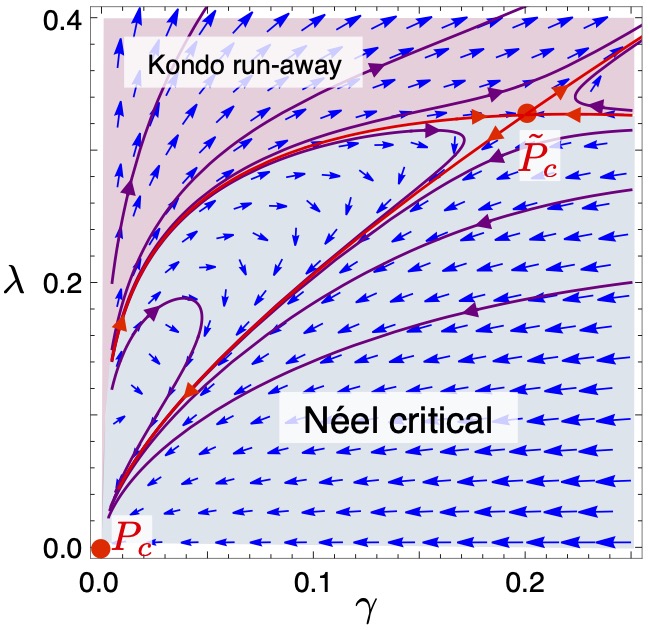
We investigate the stability of the Néel quantum critical point of two-dimensional quantum antiferromagnets, described by a
non-linear sigma model (NLSM), in the presence of a Kondo coupling to N flavours of two-component Dirac fermion fields.
The long-wavelength order parameter fluctuations are subject to Landau damping by electronic particle-hole fluctuations.
Using momentum-shell RG, we demonstrate that the Landau damping is weakly irrelevant at the Néel quantum critical point,
despite the fact that the corresponding self-energy correction dominates over the quadratic gradient terms in the IR limit.
In the ordered phase, the Landau damping increases under the RG, indicative of damped spin-wave excitations. Although the
Kondo coupling is weakly relevant, sufficiently strong Landau damping renders the Néel quantum critical point quasi-stable
for N>=4 and thermodynamically stable for N< 4. In the latter case, we identify a new multi-critical point which describes the
transition between the Néel critical and Kondo run-away regimes. The symmetry breaking at this fixed point results in the
opening of a gap in the Dirac fermion spectrum. Approaching the multi-critical point from the disordered phase, the fermionic
quasiparticle residue vanishes, giving rise to non-Fermi-liquid behavior.
- Magnetic hard-direction ordering in anisotropic Kondo systems,
M. P. Kwasigroch, Huanzhi Hu, and Frank Krüger, and A. G. Green
Phys. Rev. B 105, 224418 (2022).
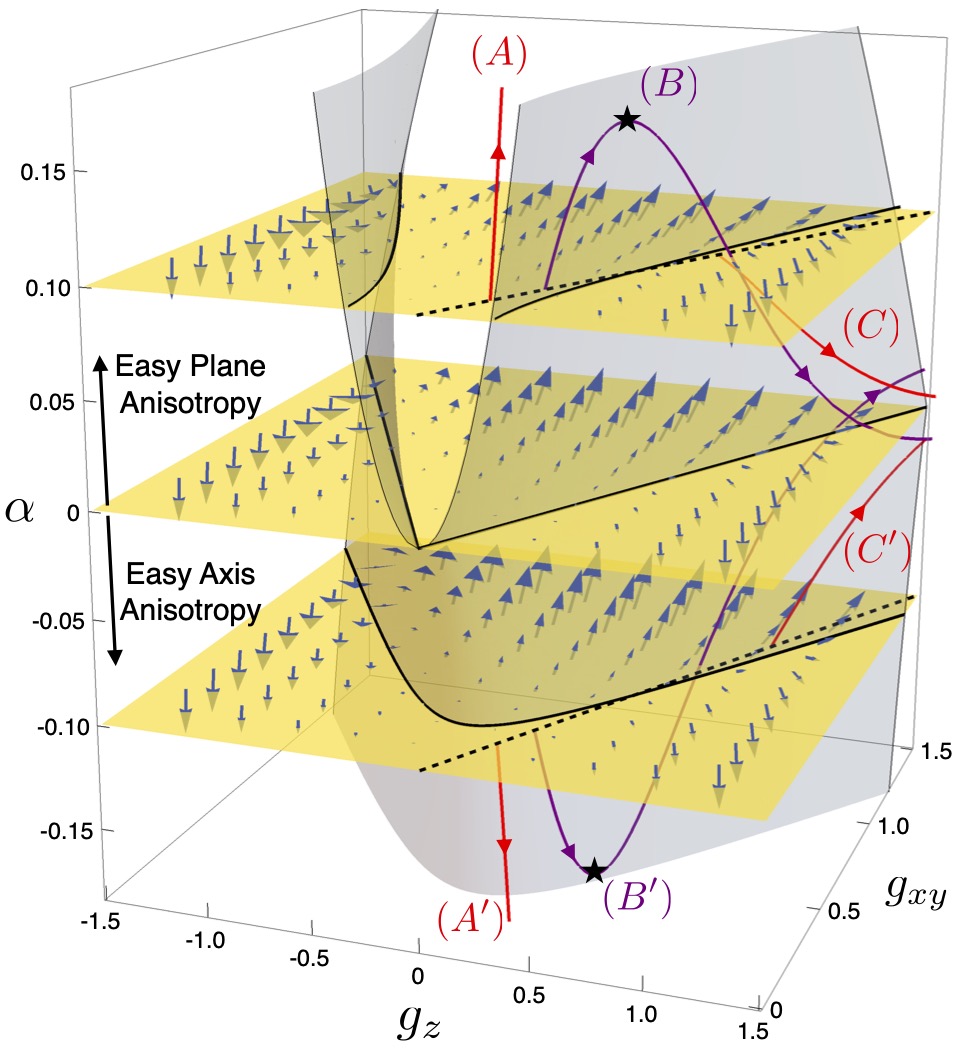
We present a generic mechanism that explains why many Kondo materials show magnetic ordering along directions that are not
favoured by the crystal-field anisotropy. Using a renormalization-group (RG) analysis of single impurity Kondo models with
single-ion anisotropy, we demonstrate that strong fluctuations above the Kondo temperature drive a moment re-orientation over
a wide range of parameters, e.g. for different spin values S and number of Kondo channels N. In tetragonal systems this can
happen for both easy-plane or easy axis anisotropy. The characteristic crossing of magnetic susceptibilities is not an artefact
of the weak-coupling RG treatment but can be reproduced in brute-force perturbation theory. Employing numerical renormalization
group (NRG), we show that for an under-screened moment (S=1, N=1) with easy-plane anisotropy, a crossing of magnetic
susceptibilities can also occur in the strong-coupling regime (below the Kondo temperature). This suggests that collective
magnetic ordering of such under-screened moments would develop along the magnetic hard axis.
Our work won the first prize in the poster competition at the International Conference on Strongly Correlated Electron Systems
(SCES2022) in Amsterdam (25-29 July 2022).

- Interplay of interactions and disorder at the charge-density wave transition of two-dimensional Dirac semimetals,
Mikolaj D. Uryszek and Frank Krüger,
Phys. Rev. B 105, 075143 (2022).
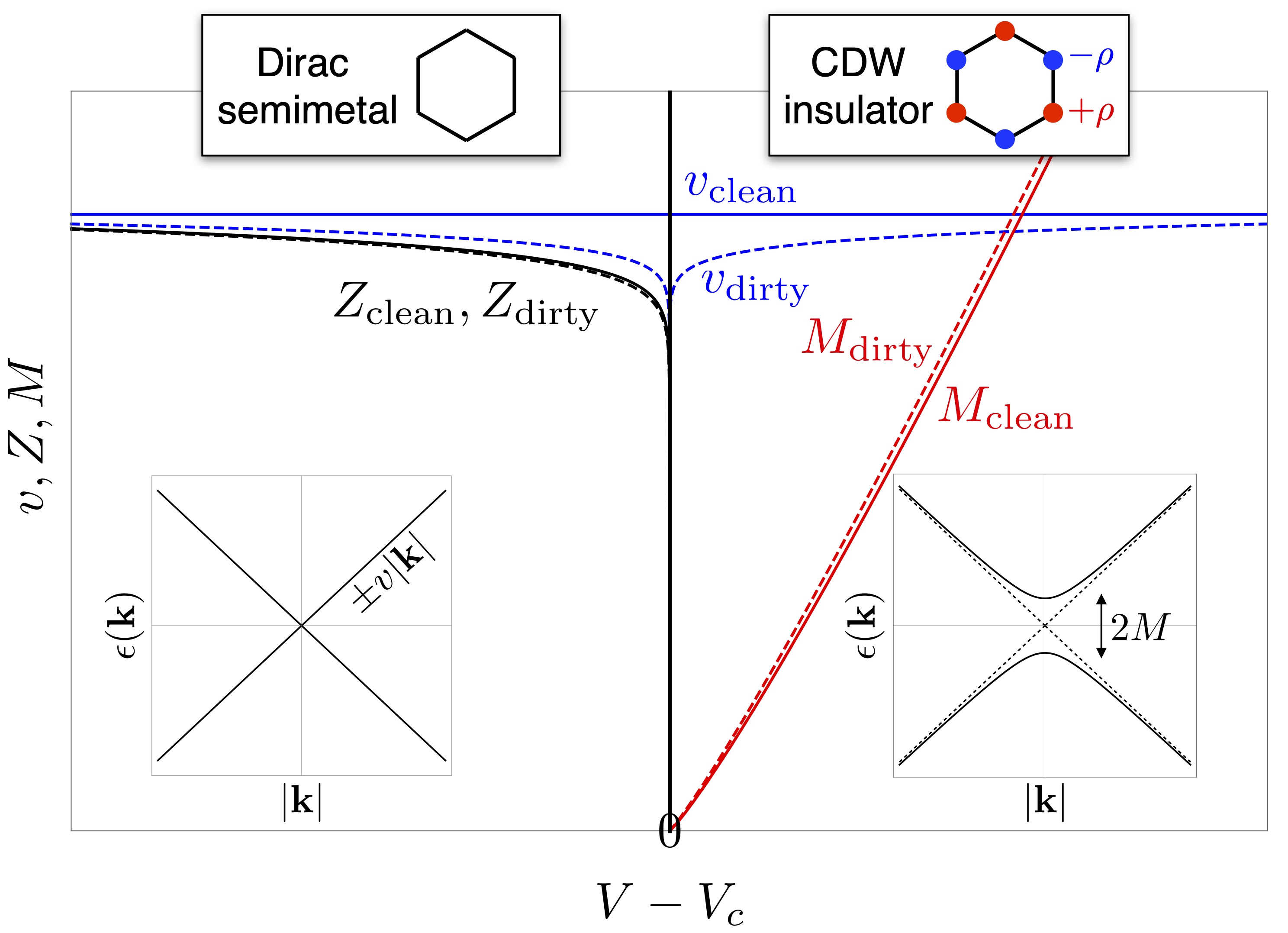
We consider the effects of weak quenched fermionic disorder on the quantum-phase transition between the Dirac semimetal and
charge density wave (CDW) insulator in two spatial dimensions. The symmetry breaking transition is described by the
Gross-Neveu-Yukawa (GNY) theory of Dirac fermions coupled to an Ising order parameter field. Treating the disorder using the
replica method, we consider chemical potential, vector potential (gauge), and random mass disorders, which all arise from
non-magnetic charge impurities. We self-consistently account for the Landau damping of long-wavelength order-parameter
fluctuations by using the non-perturbative RPA re-summation of fermion loops, and compute the renormalization-group (RG)
flow to leading order in the disorder strength and 1/N (N the number of Dirac fermion flavors). We find two fixed points,
the clean GNY critical point which is stable against weak disorder, and a dirty GNY multi-critical point, at which the chemical
potential disorder is finite and the other forms of disorder are irrelevant. We investigate the scaling of physical observables at
this finite-disorder multi-critical point which breaks Lorentz invariance and gives rise to distinct non-Fermi liquid behavior.
- Non-Fermi liquid behavior below the Néel temperature in the frustrated heavy fermion magnet UAu2,
Christopher D. O'Neill, Julian L. Schmehr, Harry D. J. Keen, Luke Pritchard Cairns, Dmitry A. Sokolov,
Andreas Hermann, Didier Wermeille, Pascal Manuel, Frank Krüger, and Andrew D. Huxley
Proceedings of the National Academy of Sciences, Dec 2021, 118 (49) e2102687118.
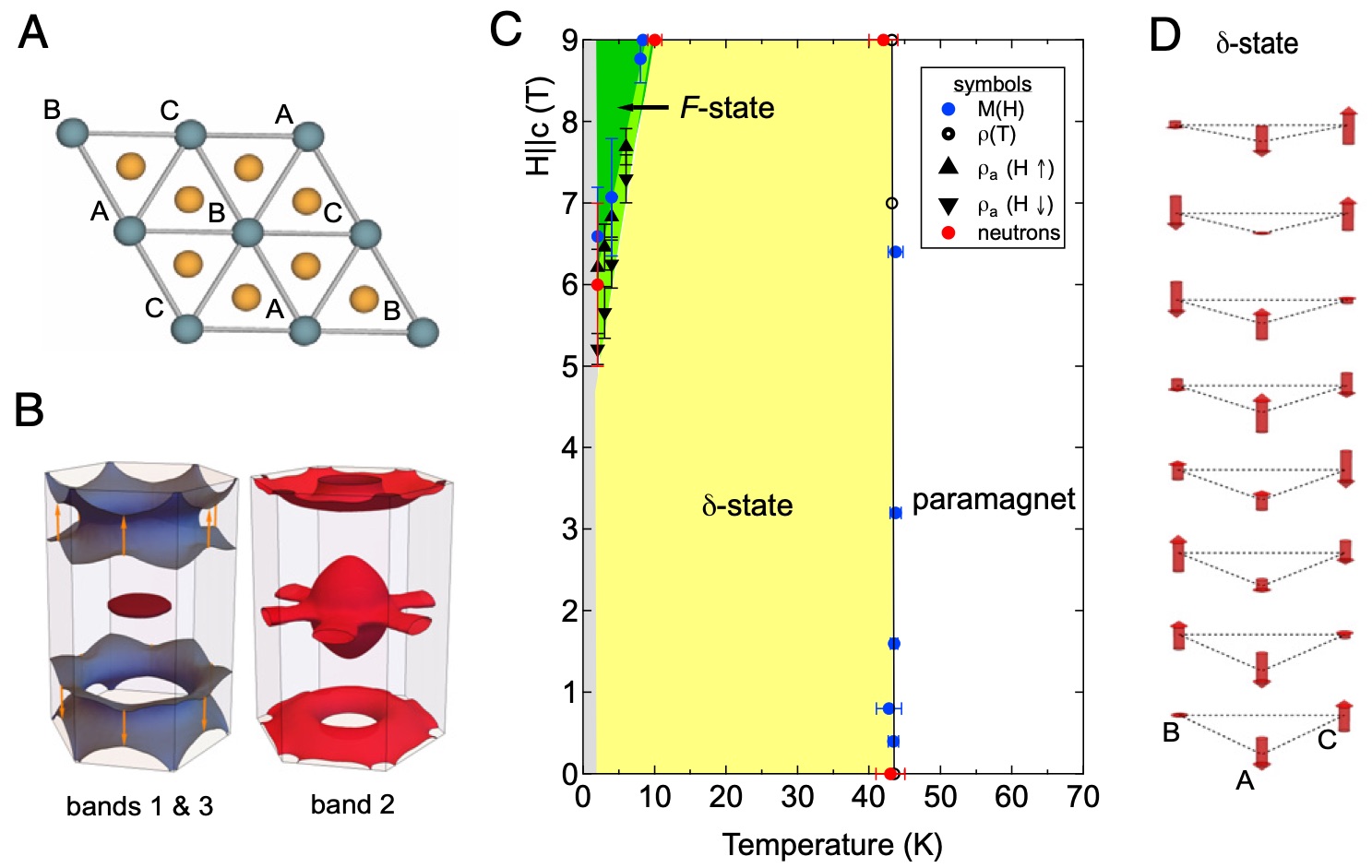
The term Fermi liquid is almost synonymous with the metallic state. The association is known to break down at quantum critical
points (QCPs), but these require precise values of tuning parameters, such as pressure and applied magnetic field, to exactly
suppress a continuous phase transition temperature to the absolute zero. Three-dimensional non-Fermi liquid states, apart from
superconductivity, that are unshackled from a QCP are much rarer and are not currently well understood. Here, we report that the
triangular lattice system uranium diauride (UAu2) forms such a state with a non-Fermi liquid low-temperature heat capacity
C/T~ log(1/T) and electrical resistivity ρ(T) - ρ(0) ~ T1.35 far below its Néel temperature. The magnetic order itself has a novel
structure and is accompanied by weak charge modulation that is not simply due to magnetostriction. The charge modulation
continues to grow in amplitude with decreasing temperature, suggesting that charge degrees of freedom play an important role
in the non-Fermi liquid behavior. In contrast with QCPs, the heat capacity and resistivity we find are unusually resilient in
magnetic field. Our results suggest that a combination of magnetic frustration and Kondo physics may result in the emergence
of this novel state.
- Field-Induced Modulated State in the Ferromagnet PrPtAl,
Christopher D. O'Neill, Gino Abdul-Jabbar, Didier Wermeille, Philippe Bourges,
Frank Krüger, and Andrew D. Huxley
Phys. Rev. Lett. 126, 197203 (2021).
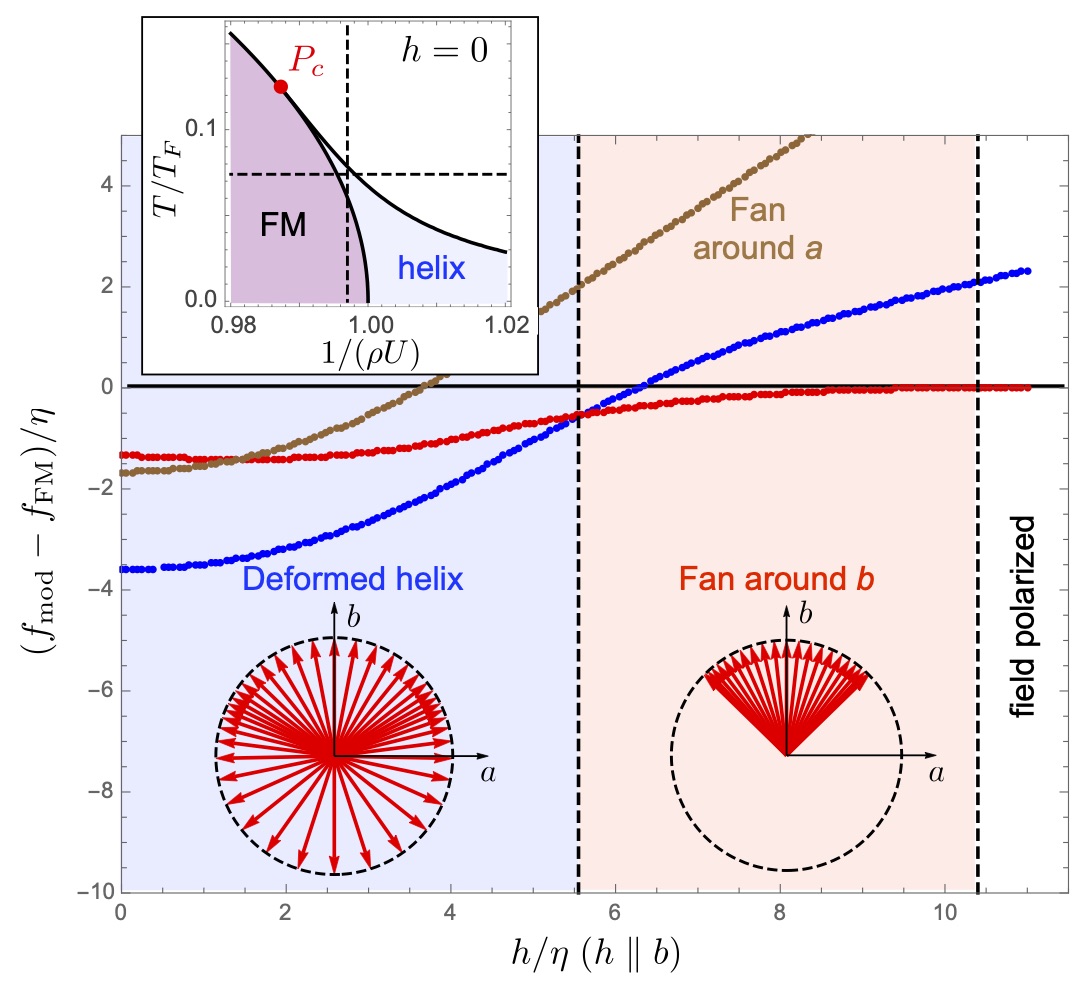
The theory of quantum order-by-disorder (QOBD) explains the formation of modulated magnetic states at the boundary
between ferromagnetism and paramagnetism in zero field. PrPtAl has been argued to provide an archetype for this.
Here, we report the phase diagram in magnetic field, applied along both the easy a-axis and hard b-axis. For field aligned
to the b-axis, we find that the magnetic transition temperatures are suppressed and at low temperature there is a single
modulated fan state, separating an easy a-axis ferromagnetic state from a field polarized state. This fan state is well
explained with the QOBD theory in the presence of anisotropy and field. Experimental evidence supporting the QOBD
explanation is provided by the large increase in the T2 coefficient of the resistivity and direct detection of enhanced
magnetic fluctuations with inelastic neutron scattering, across the field range spanned by the fan state. This shows that
the QOBD mechanism can explain field induced modulated states that persist to very low temperature.
- Fermionic criticality of anisotropic nodal point semimetals away from the upper critical dimension:
exact 1/Nf exponents,
Mikolaj D. Uryszek, Frank Krüger and Elliot Christou
Phys. Rev. Research 2, 043265 (2020).
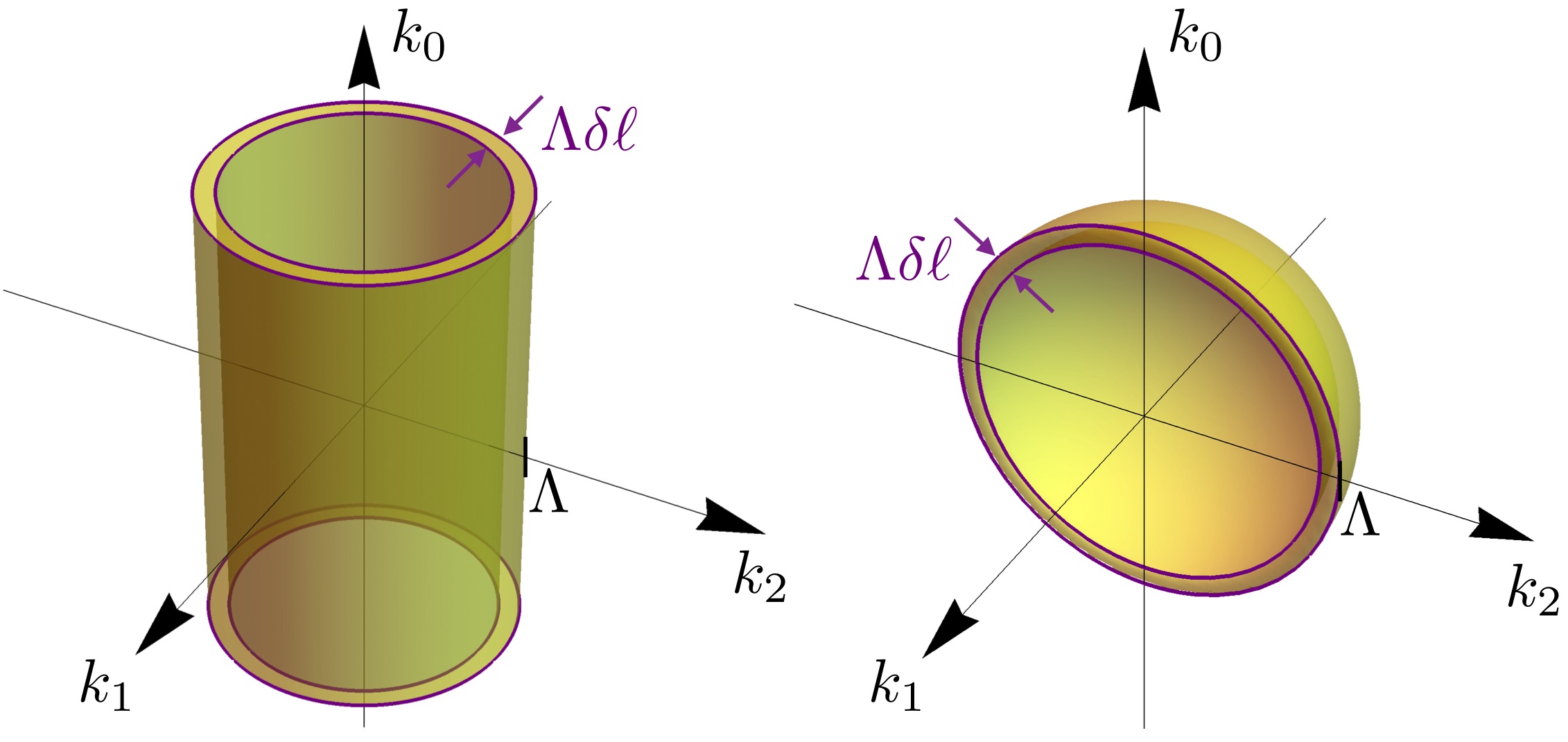
We consider the fermionic quantum criticality of anisotropic nodal point semimetals in d = dL + dQ spatial dimensions that
disperse linearly in dL dimensions, and quadratically in the remaining dQ dimensions. When subject to strong interactions,
these systems are susceptible to semimetal-insulator transitions concurrent with spontaneous symmetry breaking. Such quantum
critical points are described by effective field theories of anisotropic nodal fermions coupled to dynamical order parameter fields.
We analyze the universal scaling in the physically relevant spatial dimensions, generalizing to a large number Nf of fermion
flavors for analytic control. Landau damping by gapless fermionic excitations gives rise to non-analytic self-energy corrections
to the bosonic order-parameter propagator that dominate the long-wavelength behavior. We show that perturbative momentum
shell RG leads to non-universal, cutoff dependent results, as it does not correctly account for this non-analytic structure. In turn,
using a completely general soft cutoff formulation, we demonstrate that the correct IR scaling of the dressed bosonic propagator
can be deduced by enforcing that results are independent of the cutoff scheme. Using this soft cutoff approach, we compute the
exact critical exponents for anisotropic semi-Dirac fermions (dL=1, dQ=1) to leading order in 1/Nf, and to all loop orders.
Applying the same method to relativistic Dirac fermions, we reproduce the critical exponents obtained by other methods,
such as conformal bootstrap. Unlike in the relativistic case, where the UV-IR connection is re-established at the upper critical
dimension, non-analytic IR contributions persist near the upper critical line 2dL + dQ=4 of anisotropic nodal fermions.
We present ε-expansions in both the number of linear and quadratic dimensions. The corrections to critical exponents are
non-analytic in ε, with a functional form that depends on the starting point on the upper critical line.
- Non-linear soliton confinement in weakly coupled antiferromagnetic spin chains,
H. Lane, C. Stock, S.-W. Cheong, F. Demmel, R. A. Ewings, and F. Krüger,
Phys. Rev. B 102, 024437 (2020).
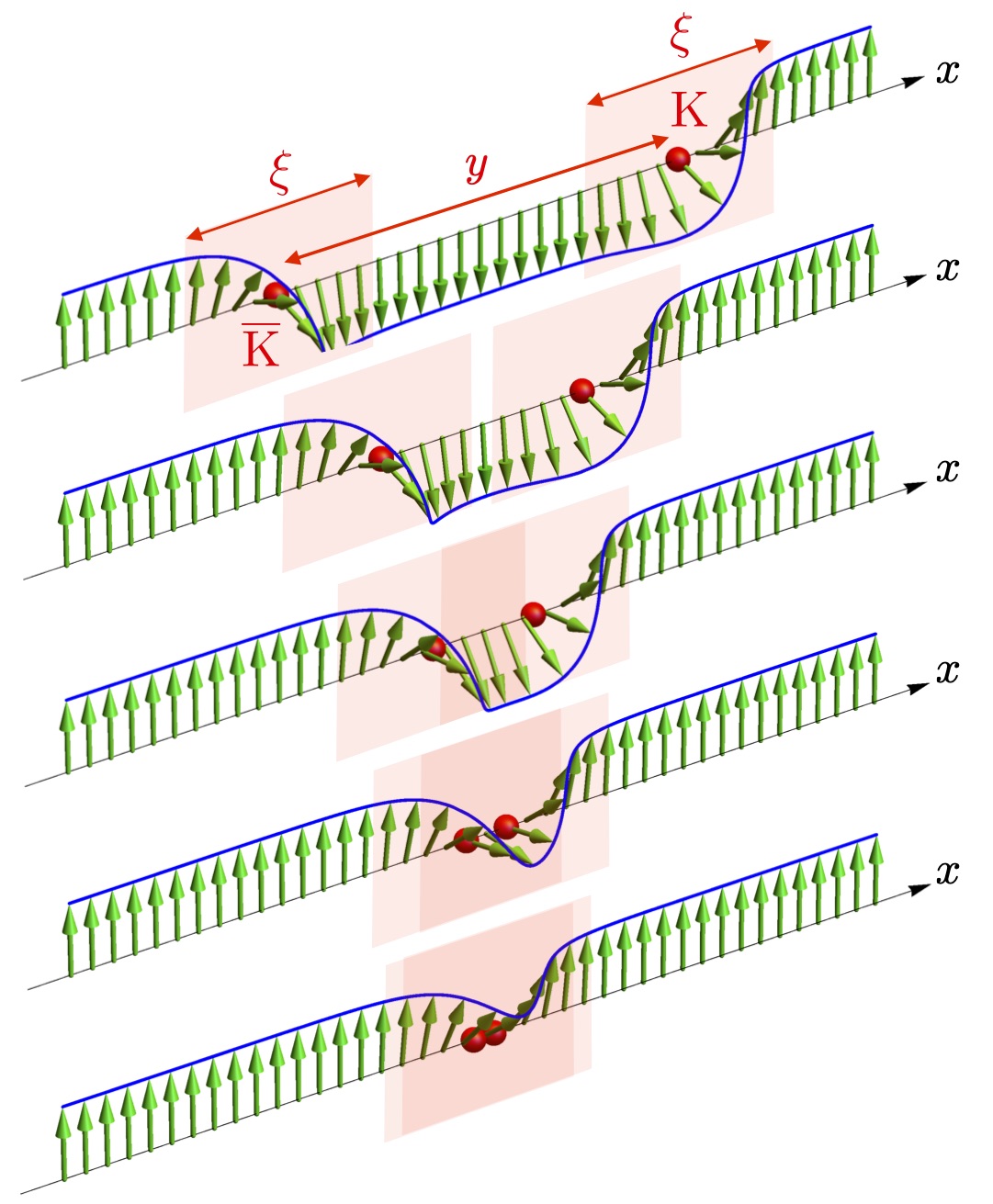
We analyze the low-energy dynamics of quasi one dimensional, large-S quantum antiferromagnets with easy-axis anisotropy,
using a semi-classical non-linear sigma model. The saddle point approximation leads to a sine-Gordon equation which supports
soliton solutions. These correspond to the movement of spatially extended domain walls. Long-range magnetic order is a
consequence of a weak inter-chain coupling. Below the ordering temperature, the coupling to nearby chains leads to an energy
cost associated with the separation of two domain walls. From the kink-antikink two-soliton solution, we compute the effective
confinement potential. At distances large compared to the size of the solitons the potential is linear, as expected for point-like
domain walls. At small distances the gradual annihilation of the solitons weakens the effective attraction and renders the potential
quadratic. From numerically solving the effective one dimensional Schrödinger equation with this non-linear confinement potential
we compute the soliton bound state spectrum. We apply the theory to CaFe2O4, an anisotropic S=5/2 magnet based upon
antiferromagnetic zig-zag chains. Using inelastic neutron scattering, we are able to resolve seven discrete energy levels for spectra
recorded slightly below the Néel temperature TN≈ 200K. These modes are well described by our non-linear confinement model
in the regime of large spatially extended solitons.
- Criticality of Dirac fermions in the presence of emergent gauge fields,
Elliot Christou, Fernando de Juan, and Frank Krüger,
Phys. Rev. B 101, 155121 (2020).
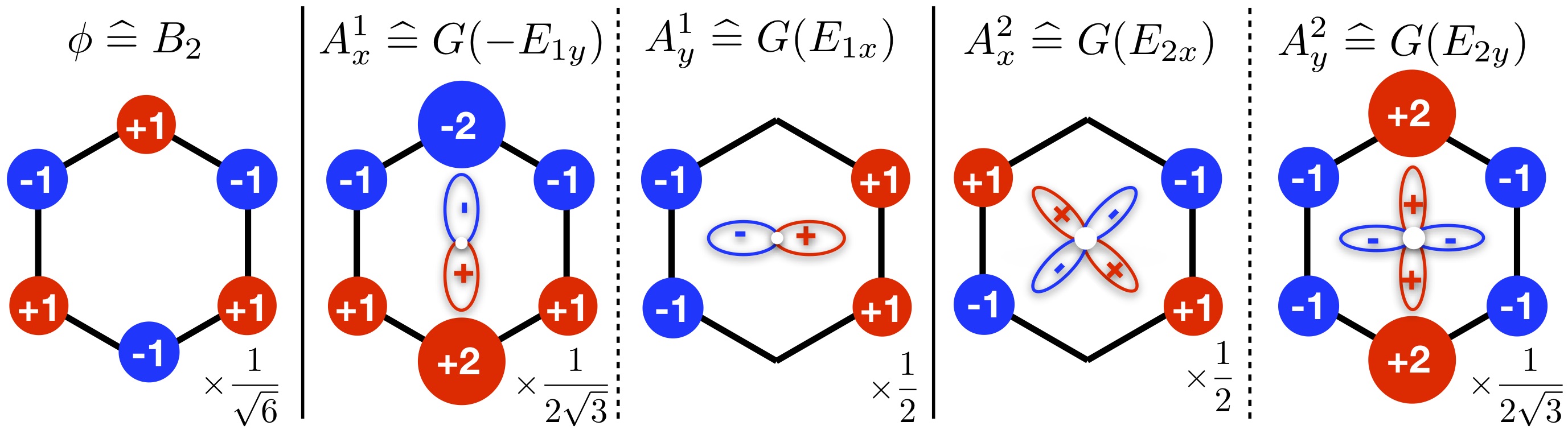
We consider spontaneous symmetry-breaking transitions of strongly interacting two-dimensional Dirac fermions minimally coupled
to mass and emergent gauge field order parameters. Using a renormalization group analysis, we show that the presence of gauge
fields leads to fermion induced quantum (multi-)criticality where the putative emergent Lorentz invariance is violated. We
illustrate this with the example of translational symmetry breaking due to charge-density wave order on the honeycomb lattice.
Finally, we identify that topological phase transitions are well described by this effective field theory.
- Quantum Criticality of Semi-Dirac Fermions in 2+1 Dimensions,
Mikolaj D. Uryszek, Elliot Christou, Akbar Jaefari, Frank Krüger, and Bruno Uchoa
Phys. Rev. B 100, 155101 (2019).
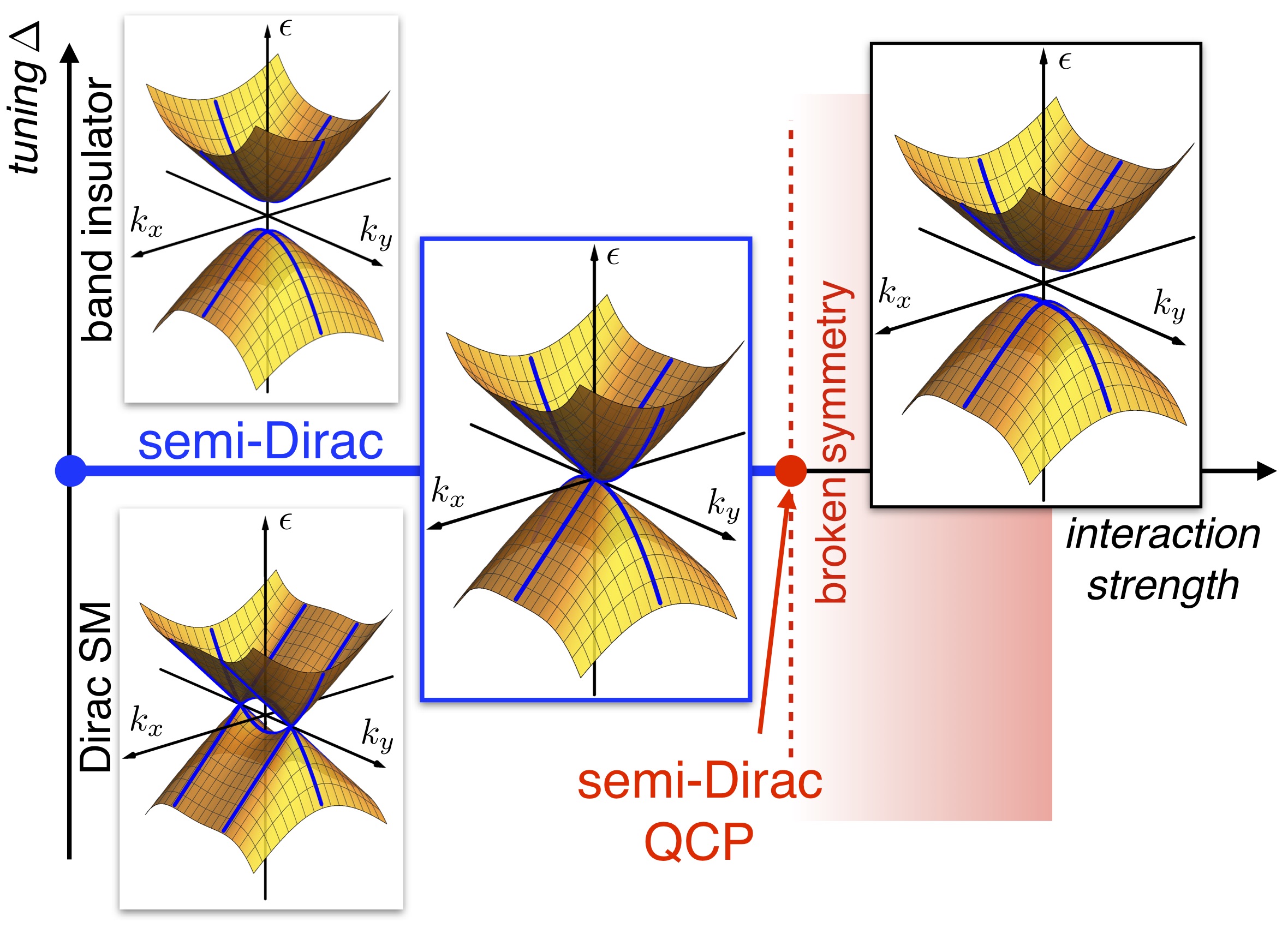
Two-dimensional semi-Dirac fermions are quasiparticles that disperse linearly in one direction and quadratically in the other.
We investigate instabilities of semi-Dirac fermions towards charge- and spin-density wave and superconducting order, driven by
short-range interactions. We analyse the critical behaviour of the Yukawa theories for the different order parameters using Wilson
momentum shell RG. We generalise to a large number Nf of fermion flavours to achieve analytic control in 2+1 dimensions and
calculate critical exponents at one-loop order, systematically including 1/Nf corrections . The latter depend on the specific form
of the bosonic IR propagator in 2+1 dimensions, which needs to be included to regularise divergencies. The 1/Nf corrections
are surprisingly small, suggesting that the expansion is well controlled in the physical dimension. The order parameter correlations
inherit the electronic anisotropy of the semi-Dirac fermions, leading to correlation lengths that diverge along the spatial directions
with distinct exponents, even at the mean-field level. We conjecture that the proximity to the critical point may stabilize novel
modulated order phases.
- Hidden Charge Order of Interacting Dirac fermions on the Honeycomb Lattices,
Elliot Christou, Bruno Uchoa, and Frank Krüger,
Phys. Rev. B 98, 161120(R) (2018).
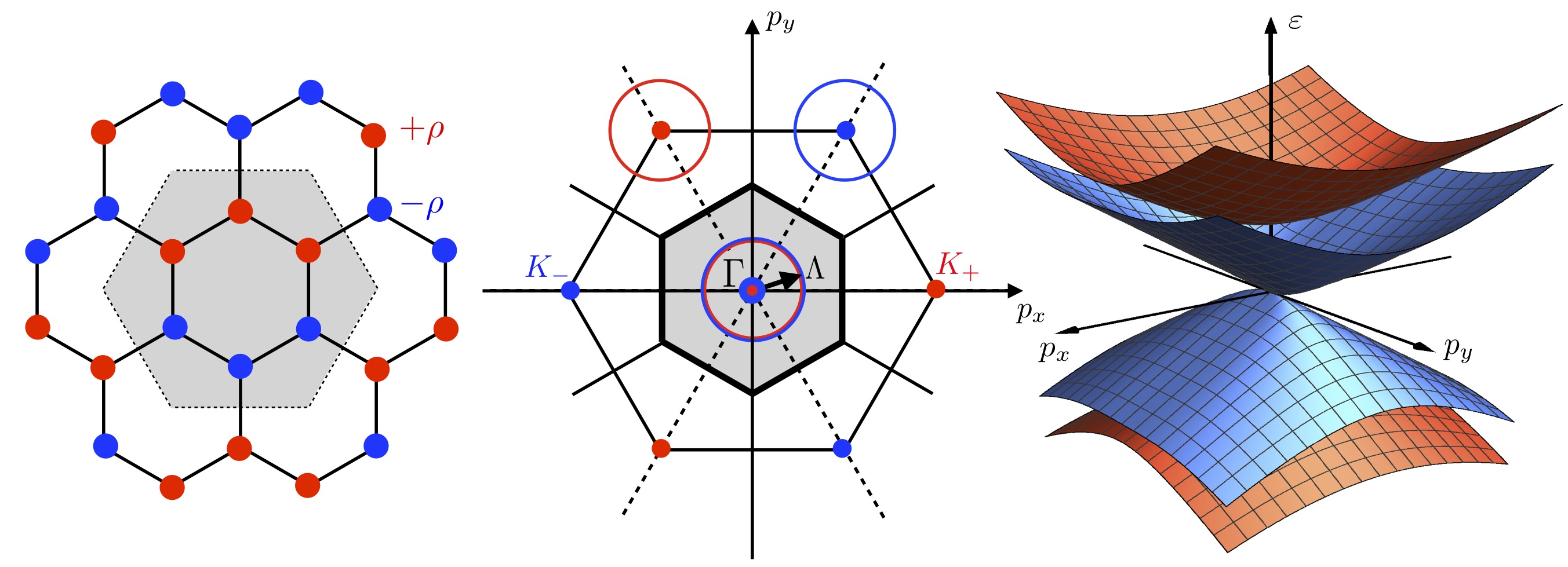
We consider the extended half-filled Hubbard model on the honeycomb lattice for second nearest neighbors interactions.
Using a functional integral approach, we find that collective fluctuations suppress topological states and instead favor charge ordering,
in agreement with previous numerical studies. However, we show that the critical point is not of the putative semimetal-Mott insulator
variety. Due to the frustrated nature of the interactions, the ground state is described by a hidden metallic charge order with semi-Dirac
excitations. We conjecture that this transition is not in the Gross-Neveu universality class.
- Quantum Order-by-Disorder in Strongly Correlated Metals,
A. G. Green, G. Conduit, and F. Krüger,
Annual Reviews of Condensed Matter Physics 9, pp. 59-77 (2018).
Entropic forces in classical many-body systems, e.g. colloidal suspensions, can lead to the formation of new phases. Quantum
fluctuations can have similar effects: spin fluctuations drive the superfluidity of Helium-3 and a similar mechanism operating in metals
can give rise to superconductivity. It is conventional to discuss the latter in terms of the forces induced by the quantum fluctuations.
However, focusing directly upon the free energy provides a useful alternative perspective in the classical case and can also be applied
to study quantum fluctuations. Villain first developed this approach for insulating magnets and coined the term order-by-disorder to
describe the observed effect. We discuss the application of this idea to metallic systems, recent progress made in doing so, and the
broader prospects for the future.
- Topological Triplon Modes and Bound States in a Shastry-Sutherland Magnet,
P. A. McClarty, F. Krüger, T. Guidi, S. F. Parker, K. Refson, A. W. Parker, D. Prabakharan, and R. Coldea
Nature Physics 13, 736 (2017).
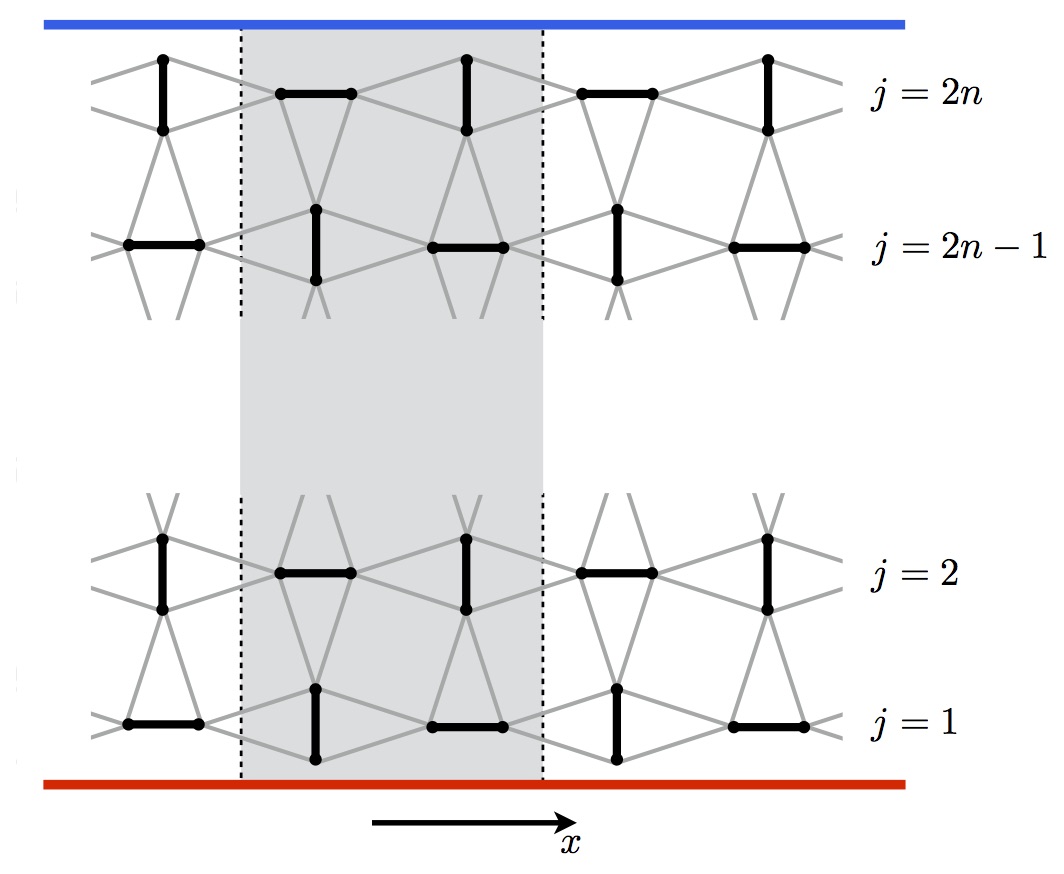
The twin discoveries of the quantum Hall effect, in the 1980's, and of topological band insulators, in the 2000's, were landmarks in
physics that enriched our view of the electronic properties of solids. In a nutshell, these discoveries have taught us that quantum
mechanical wavefunctions in crystalline solids may carry nontrivial topological invariants which have ramifications for the observable
physics. One of the side effects of the recent topological insulator revolution has been that such physics is much more widespread
than was appreciated ten years ago. For example, while topological insulators were originally studied in the context of electron
wavefunctions, recent work has led to proposals of topological insulators in bosonic systems: in photonic crystals, in the vibrational
modes of crystals, and in the excitations of ordered magnets. Here we confirm the recent proposal that, in a weak magnetic field, the
dimerized quantum magnet SrCu2(BO3)2 is a bosonic topological insulator with nonzero Chern number in the triplon bands and
topologically protected chiral edge excitations.
- Entanglement entropies and fermion signs of critical metals,
N. Kaplis, F. Krüger, and J. Zaanen
Phys. Rev. B 95, 155102 (2017).
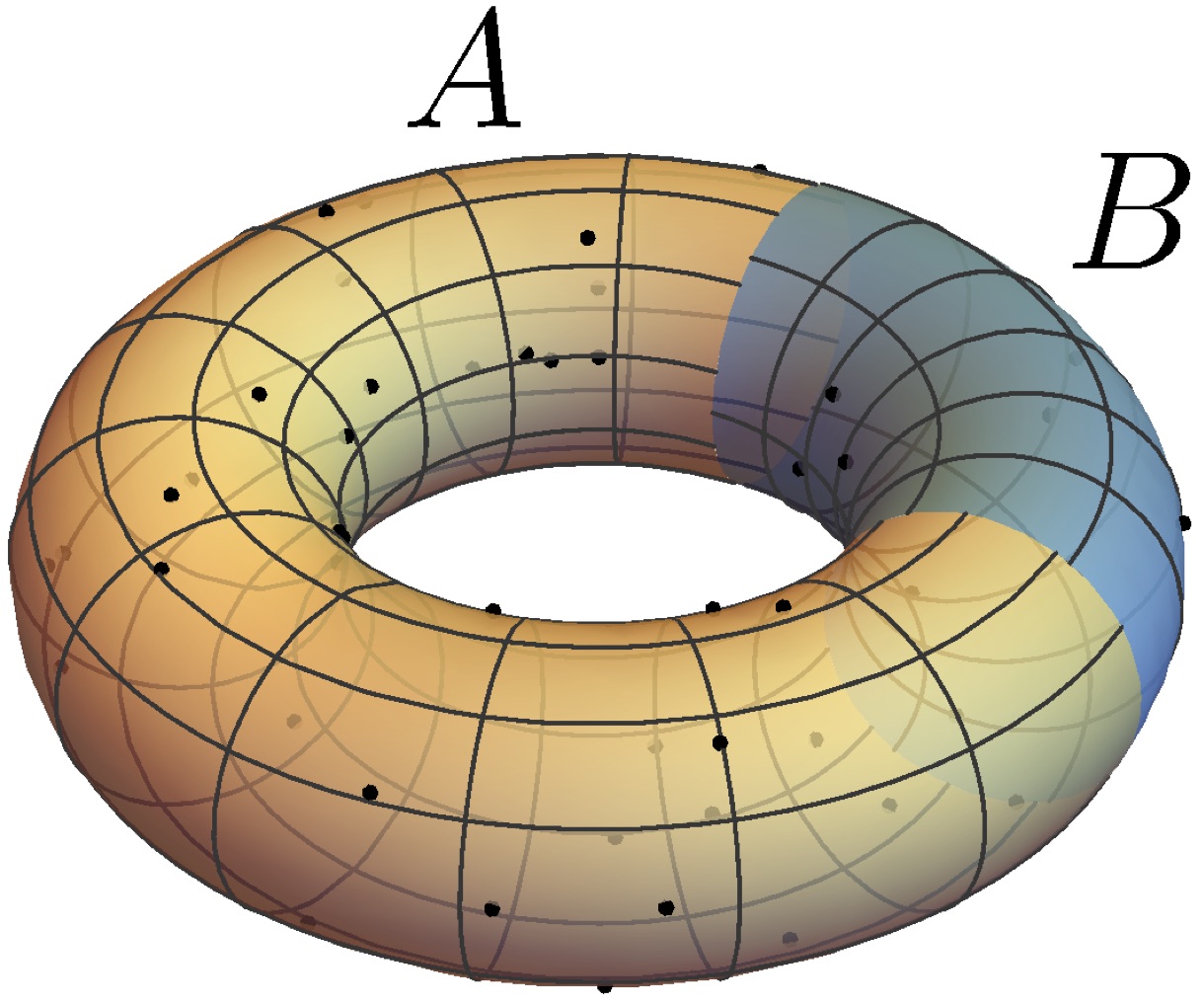
The fermion sign problem is often viewed as a sheer inconvenience that plagues numerical studies of strongly interacting electron
systems. Only recently, it has been suggested that fermion signs are fundamental for the universal behavior of critical metallic
systems and crucially enhance their degree of quantum entanglement.In this work we explore potential connections between
emergent scale invariance of fermion sign structures and scaling properties of bipartite entanglement entropies. Our analysis
is based on a wavefunction ansatz that incorporates collective, long-range backflow correlations into fermionic Slater determinants.
Such wavefunctions mimic the collapse of a Fermi liquid at a quantum critical point. Their nodal surfaces -- a representation of the
fermion sign structure in many-particle configurations space -- show fractal behavior up to a length scale ξ that diverges at a critical
backflow strength. We show that the Hausdorff dimension of the fractal nodal surface depends on ξ, the number of fermions,
and the exponent of the backflow. For the same wavefunctions we numerically calculate the second Rényi entanglement entropy S2.
Our results show a cross-over from volume scaling, S2 ~ℓ^θ (θ=2 in d=2 dimensions), to the characteristic Fermi-liquid behavior
S2 ~ ℓ ln ℓ on scales larger than ξ. We find that volume scaling of the entanglement entropy is a robust feature of critical backflow
fermions, independent of the backflow exponent and hence the fractal dimension of the scale invariant sign structure.
- Stability of a spin-triplet nematic state near to a quantum critical point,
G. Hannappel, C. J. Pedder, F. Krüger, and A. G. Green
Phys. Rev. B 93, 235105 (2016).
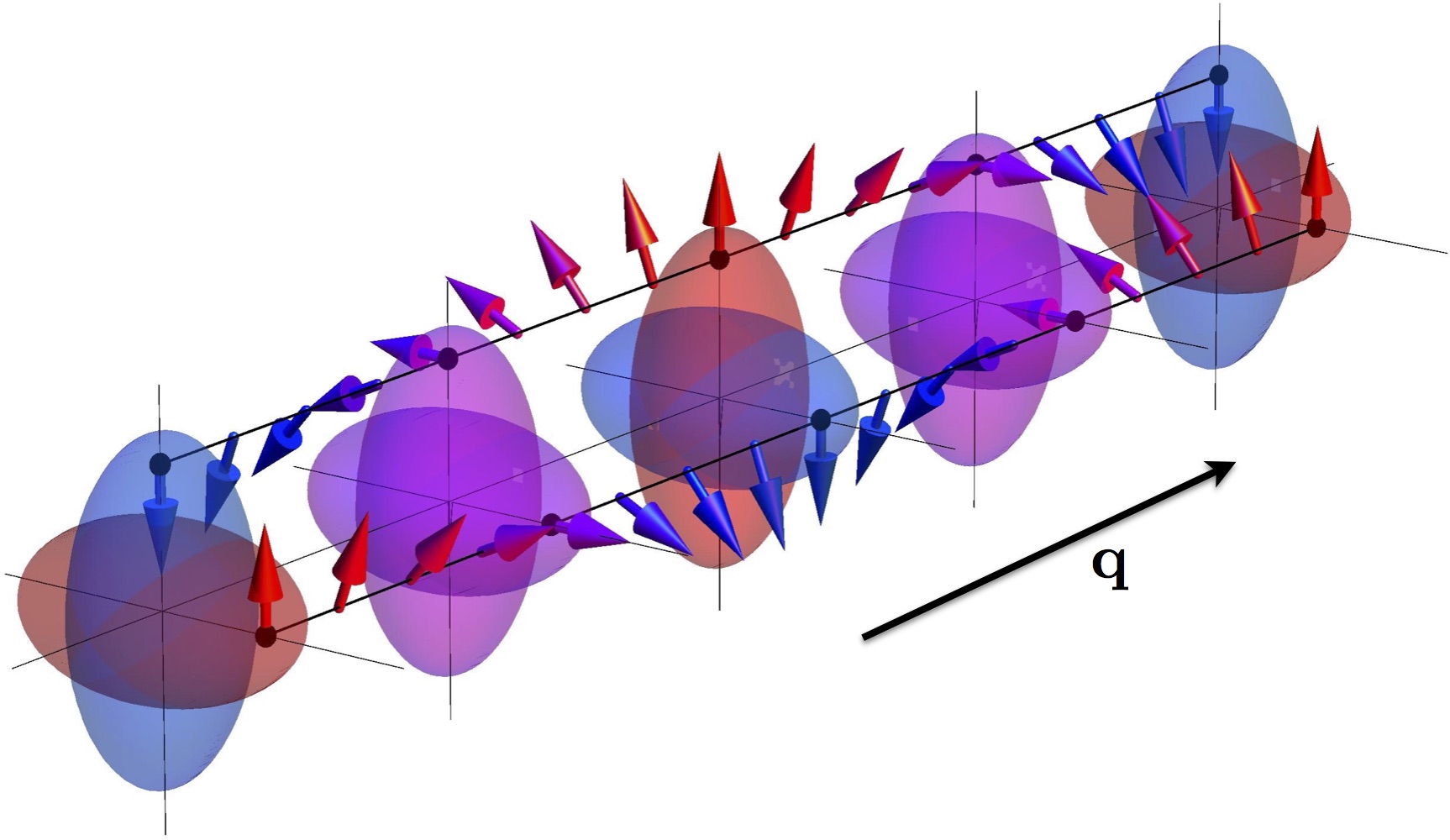
We analyze a model of itinerant electrons interacting through a quadrupole density-density repulsion in three dimensions. At the
mean field level, the interaction drives a continuous Pomeranchuk instability towards d-wave, spin-triplet nematic order, which
simultaneously breaks the SU(2) spin-rotation and spatial rotational symmetries. This order results in spin antisymmetric, elliptical
deformations of the Fermi surfaces of up and down spins. We show that the effects of quantum fluctuations are similar to those in
metallic ferromagnets, rendering the nematic transition first-order at low temperatures. Using the fermionic quantum order-by-disorder
approach to self-consistently calculate fluctuations around possible modulated states, we show that the first-order transition is
pre-empted by the formation of a nematic state that is intertwined with a helical modulation in spin space. Such a state is closely
related to d-wave bond density wave order in square-lattice systems. Moreover, we show that it may coexist with a modulated,
p-wave superconducting state.
- Incommensurate spin-density-wave antiferromagnetism in CeRu2Al2B,
A. Bhattacharyya, D. D. Khalyavin, F. Krüger, D. T. Adroja, A. M. Strydom, W. A. Kockelmann, and A. D. Hillier,
Phys. Rev. B 93, 060410(R) (2016).
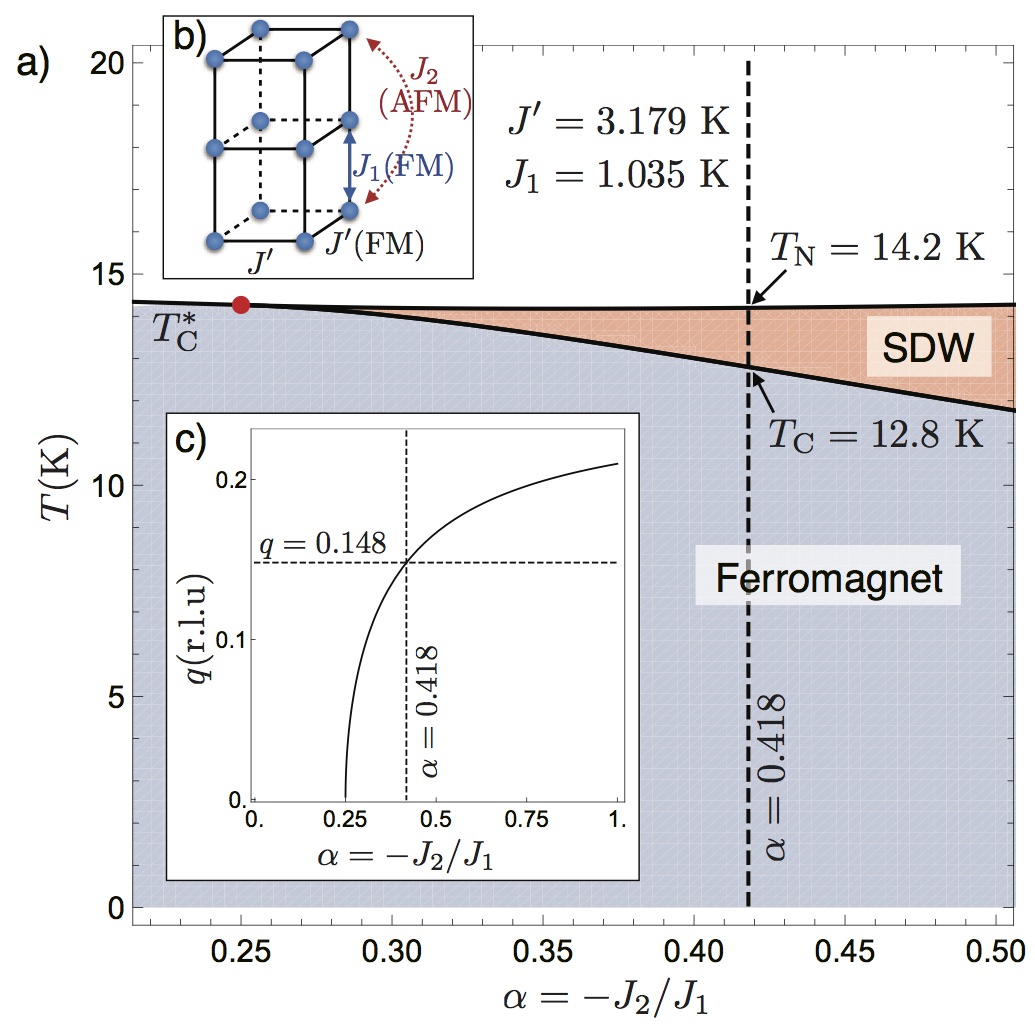
The newly discovered Ising-type ferromagnet CeRu2Al2B exhibits an additional phase transition at TN= 14.2 K before going to the
ferromagnetic ground state at TC = 12.8 K. We clarify the nature of this transition through high resolution neutron diffraction
measurements. The data reveals the presence of a longitudinal incommensurate spin-density wave (SDW) in the temperature range
between TC and TN. The propagation vector q~(0,0,0.148) is nearly temperature independent in this region and discontinuously
locks into q=0 at TC. Mean-field calculations of an effective Ising model indicate that the modulated SDW phase is stabilized by
a strong competition between ferromagnetic and antiferromagnetic exchange interactions. This makes CeRu2Al2B a particularly
attractive model system to study the global phase diagram of ferromagnetic heavy-fermion metals under influence of magnetic
frustration.
- Bose and Mott Glass Phases in Dimerized Quantum Antiferromagnets,
S. J. Thomson and F. Krüger,
Phys. Rev. B 92, 180201(R) (2015).
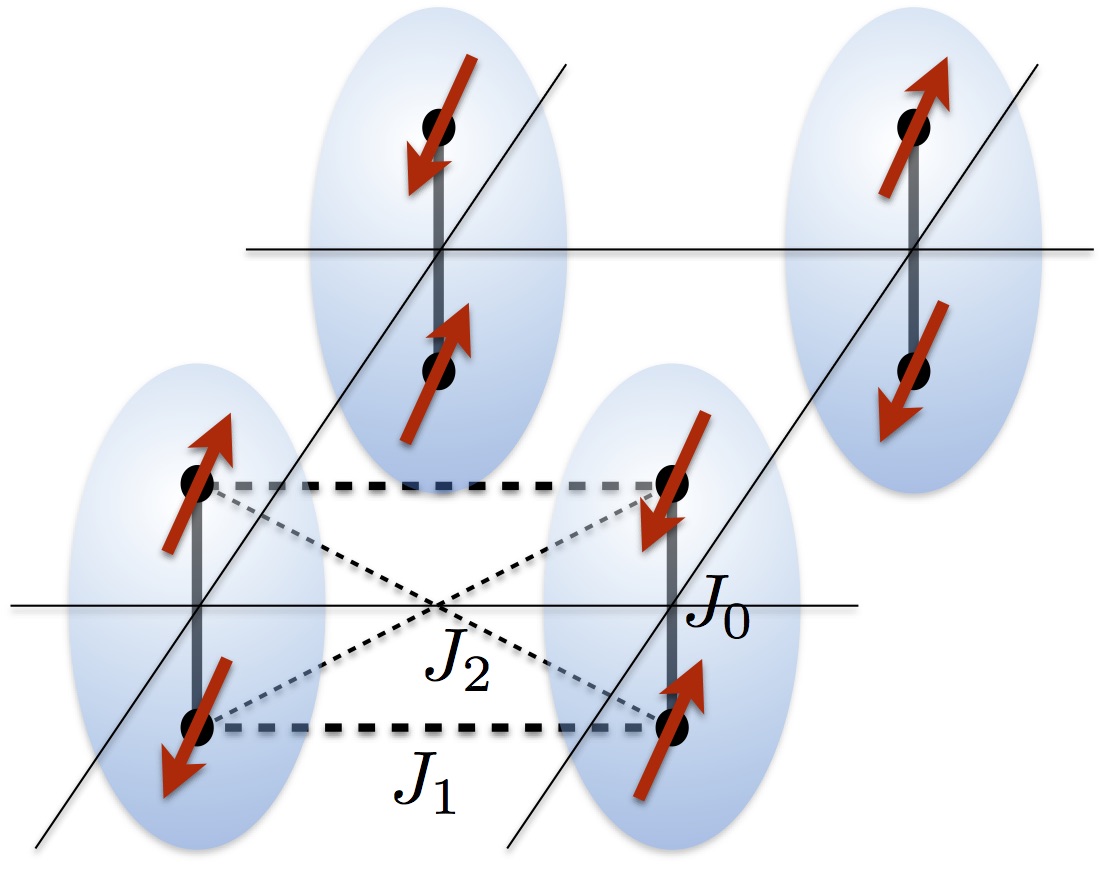
We examine the effects of disorder on dimerized quantum antiferromagnets in a magnetic field, using the mapping to a lattice gas
of hard-core bosons with finite-range interactions. Combining a strong-coupling expansion, the replica method, and a one-loop
renormalization group analysis, we investigate the nature of the glass phases formed. We find that away from the tips of the Mott lobes,
the transition is from a Mott insulator to a compressible Bose glass, however the compressibility at the tips is strongly suppressed. We
identify this finding with the presence of a rare Mott glass phase not previously described by any analytic theory for this model and
demonstrate that the inclusion of replica symmetry breaking is vital to correctly describe the glassy phases. This result suggests that
the formation of Bose and Mott glass phases is not simply a weak localization phenomenon but is indicative of much richer physics.
We discuss our results in the context of both ultracold atomic gases and spin-dimer materials.
- Modulated magnetism in PrPtAl,
G. Abdul-Jabbar, D. A. Sokolov, C. O'Neill, C. Stock, D. Wermeille, F. Demmel, F. Krüger, A. G. Green,
F. Levy-Bertrand, B. Grenier, and A. Huxley,
Nature Physics 11, 321 (2015).
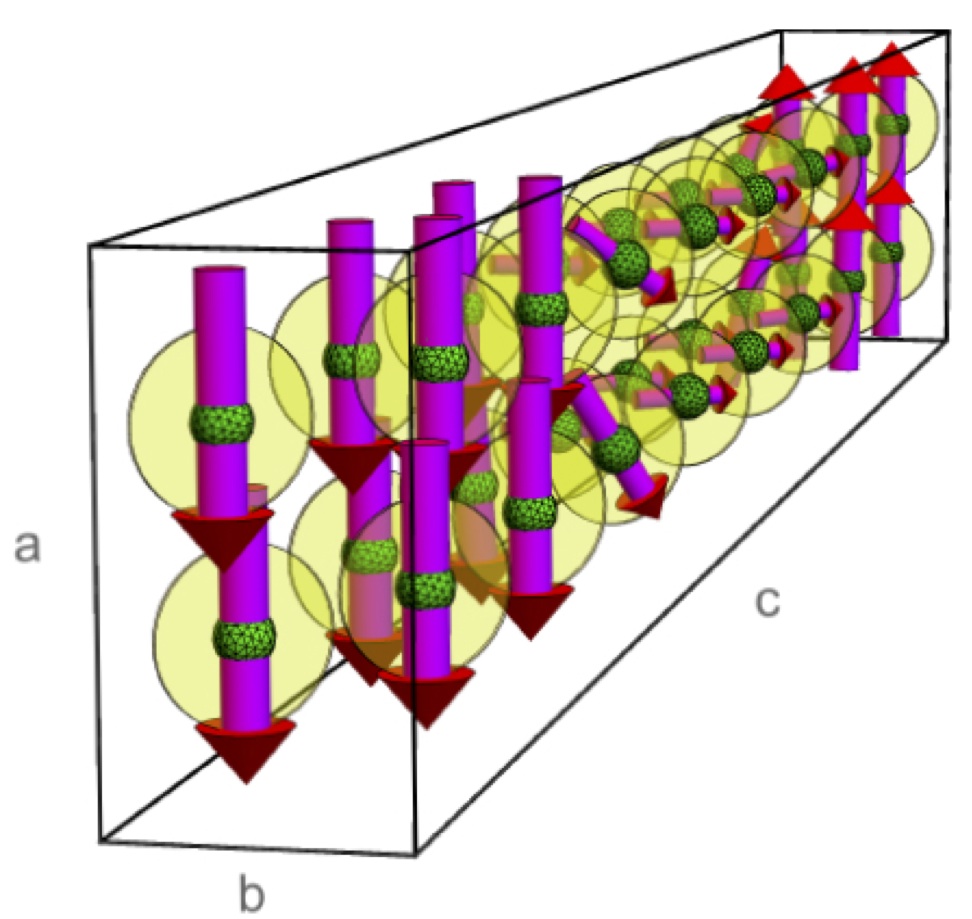
The transition between paramagnetism and ferromagnetism is the paradigm for a continuous phase transition at finite temperature.
When such a transition is tuned to zero temperature in clean materials, the growth of low energy zero-point fluctuations potentially
drives an array of phenomena, including the formation of novel states such as non-conventional superconductivity. Experimentally,
the growth of the fluctuations is however curtailed and the transition becomes discontinuous as its temperature is reduced. This
is understood to arise from non-analytic corrections to the free energy that always occur. In a recent theory changes of the excitation
spectrum are self-consistently considered alongside the ground state. This analysis reveals that a transition to a new state may be
an alternative outcome. Since the excitation spectrum (the "disorder") is pivotal to promoting the new "order" this mechanism is
referred to as "order by disorder". Here, we report the discovery of modulated order in PrPtAl, consistent with complex spirals, at
the boundary between paramagnetism and ferromagnetism that is the first clear experimental realisation of such a state.
- Symmetry of re-entrant tetragonal phase in Ba(1-x)Na(x)Fe(2)As(2): magnetic versus orbital ordering mechanism,
D.D. Khalyavin, S.W. Lovesey, P. Manuel, F. Krüger, S. Rosenkranz, J.M. Allred, O. Chmaissem, and R. Osborn,
Phys. Rev. B 90, 174511 (2014).
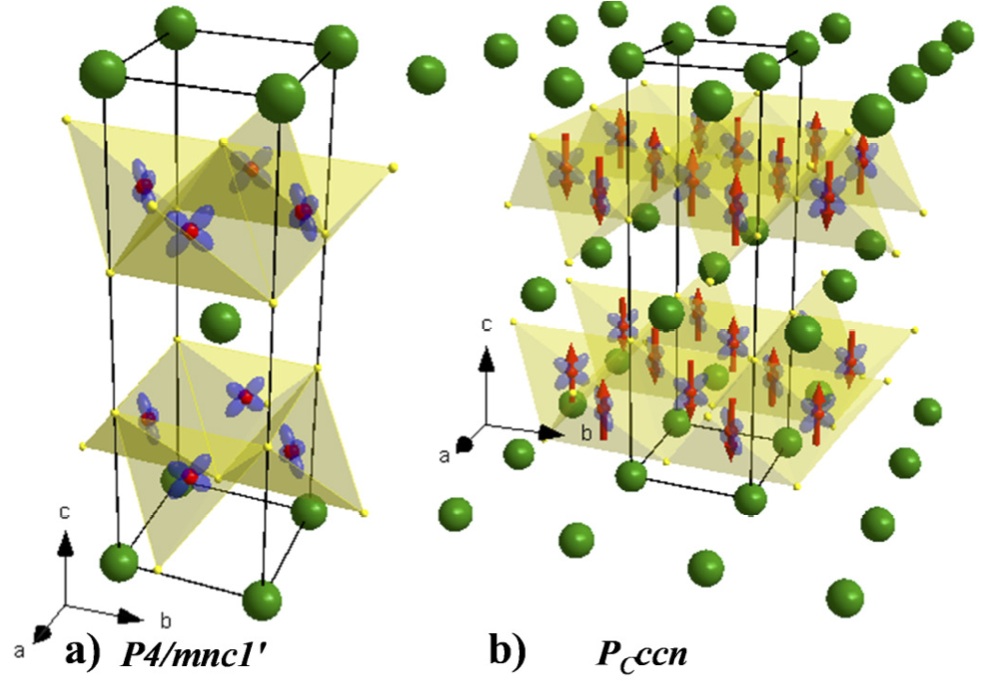
Magneto-structural phase transitions in Ba(1-x)A(x)xFe(2)As(2) (A = K, Na) materials are discussed for both magnetically and orbitally
driven mechanisms, using a symmetry analysis formulated within the Landau theory of phase transitions. Both mechanisms predict
identical orthorhombic space-group symmetries for the nematic and magnetic phases observed over much of the phase diagram, but
they predict different tetragonal space-group symmetries for the newly discovered re-entrant tetragonal phase in Ba(1-x)Na(x)xFe(2)As(2)
(x ~ 0.24-0.28). In a magnetic scenario, magnetic order with moments along the c-axis, as found experimentally, does not allow any type
of orbital order, but in an orbital scenario, we have determined two possible orbital patterns, specified by P4/mnc1' and I4221' space
groups, which do not require atomic displacements relative to the parent I4/mmm1' symmetry and, in consequence, are indistinguishable
in conventional diffraction experiments. We demonstrate that the three possible space groups are however, distinct in resonant X-ray
Bragg diffraction patterns created by Templeton-Templeton scattering. This provides an experimental method of distinguishing between
magnetic and orbital models.
- Fluctuation driven magnetic hard-axis ordering in metallic ferromagnets,
F. Krüger, C. J. Pedder, and A. G. Green,
Phys. Rev. Lett. 113, 147001 (2014).
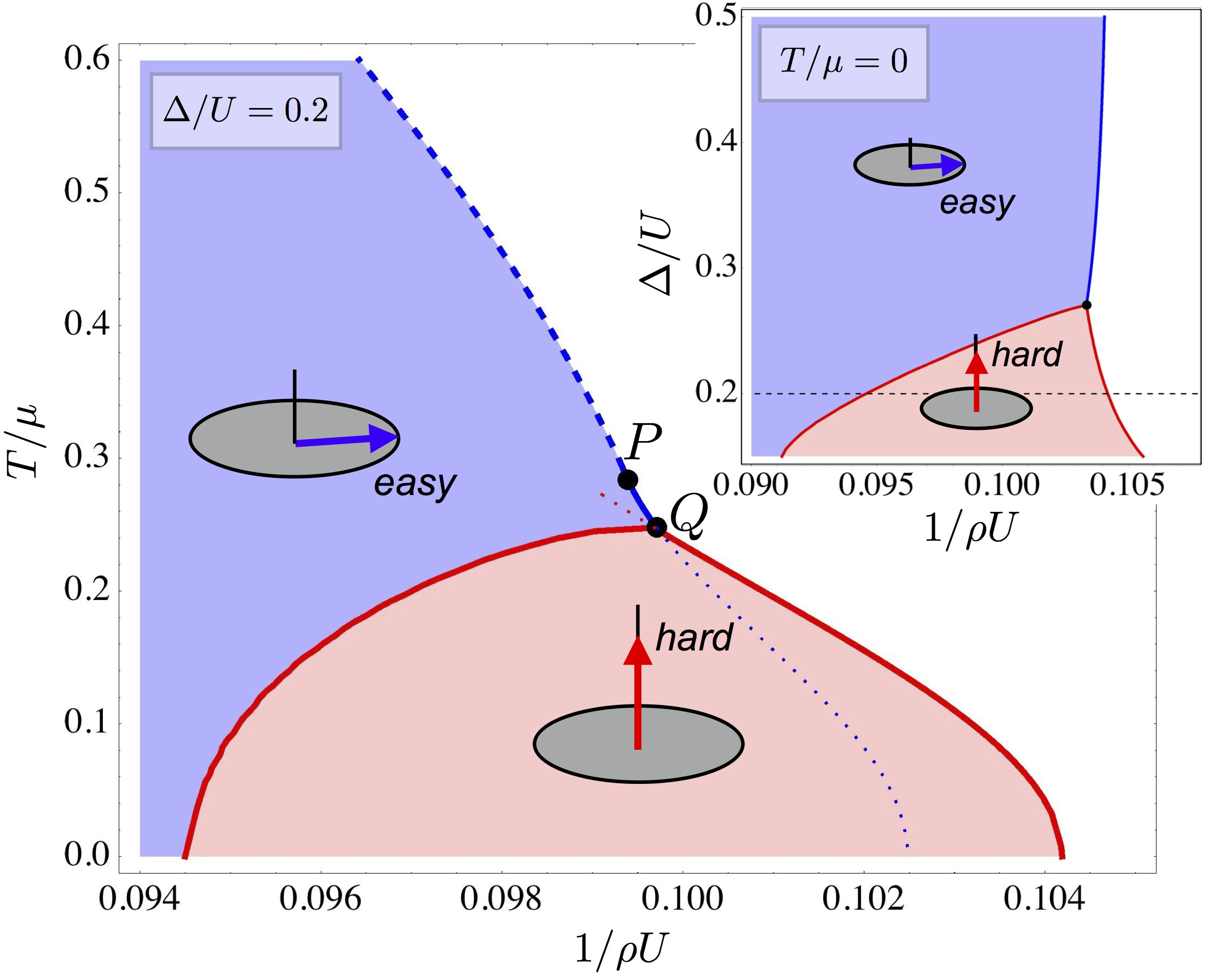
We demonstrate that the interplay between soft electronic particle-hole fluctuations and magnetic anisotropies can drive ferromagnetic
moments to point along a magnetic hard axis. As a proof of concept, we show this behavior explicitly for a generic two-band model with
local Coulomb and Hund's interactions, and a spin-orbit-induced easy plane anisotropy. The phase diagram is calculated within the
fermionic quantum order-by-disorder approach, which is based on a self-consistent free-energy expansion around a magnetically ordered
state with unspecified orientation. Quantum fluctuations render the transition of the easy-plane ferromagnet first-order below a tricritical
point. At even lower temperatures, directionally dependent transverse fluctuations dominate the magnetic anisotropy and the moments
flip to lie along the magnetic hard axis. We discuss our findings in the context of recent experiments that show this unusual ordering
along the magnetic hard direction.
- Replica symmetry breaking in the Bose glass,
S. J. Thomson and F. Krüger,
EPL (Europhysics Letters) 108, 30002 (2014).
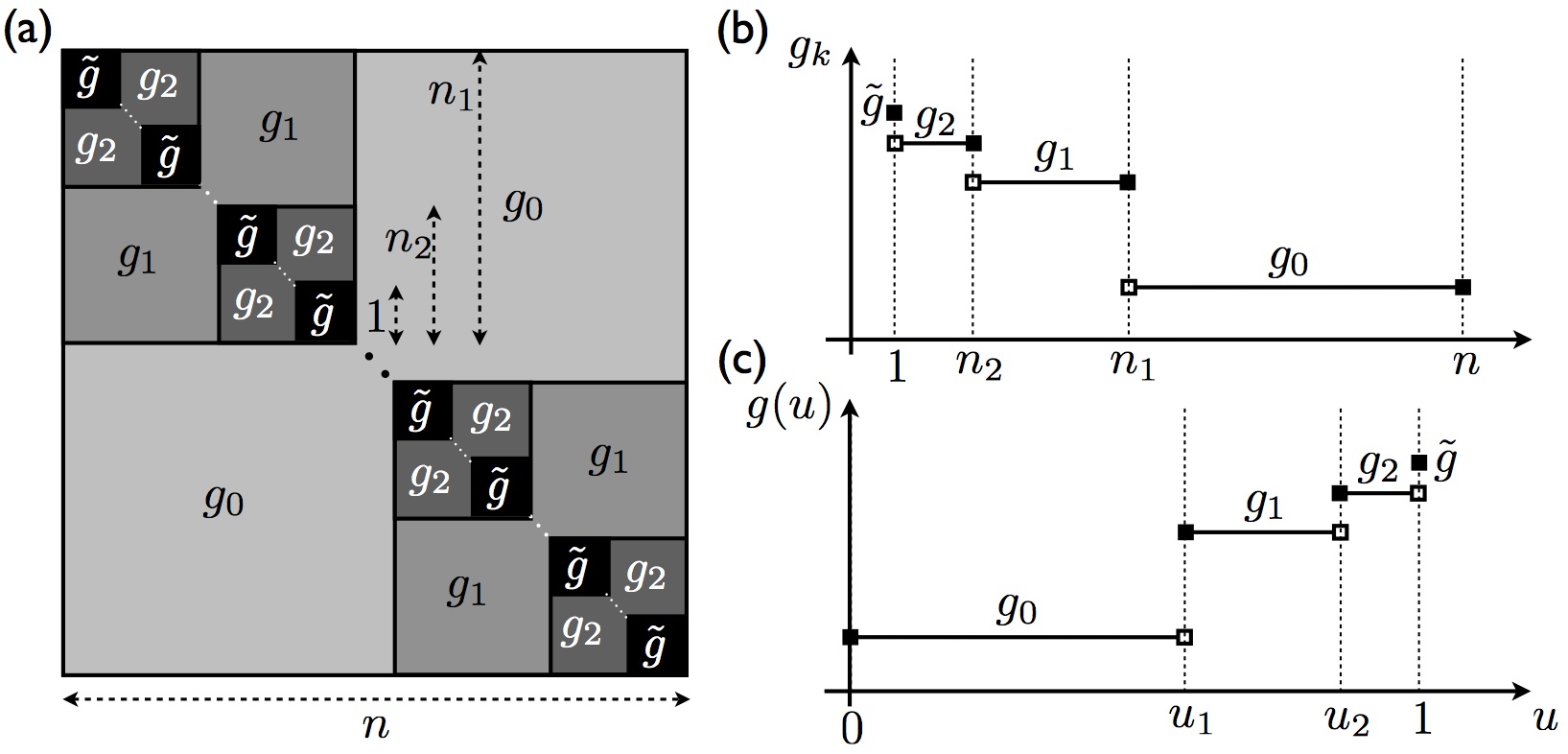
We investigate the nature of the Bose glass phase of the disordered Bose-Hubbard model in d>2 and demonstrate the existence of a
glass-like replica symmetry breaking (RSB) order parameter in terms of particle number fluctuations. Starting from a strong-coupling
expansion around the atomic limit, we study the instability of the Mott insulator towards the formation of a Bose glass. We add some
infinitesimal RSB, following the Parisi hierarchical approach in the most general form, and observe its flow under the momentum-shell
renormalization group scheme. We find a new fixed point with one-step RSB, corresponding to the transition between the Mott insulator
and a Bose glass phase with hitherto unseen RSB. The susceptibility associated to infinitesimal RSB perturbation in the Mott insulator
is found to diverge at the transition with an exponent of gamma=1/d. Our findings are consistent with the expectation of glassy behavior
and the established breakdown of self-averaging. We discuss the possibility of measuring the glass-like order parameter in optical
lattice experiments as well as in certain spin systems that are in the same universality class as the Bose-Hubbard model.
- Resummation of fluctuations near ferromagnetic quantum critical points,
C. J. Pedder, F. Krüger, and A. G. Green,
Phys. Rev. B 88, 165109 (2013).
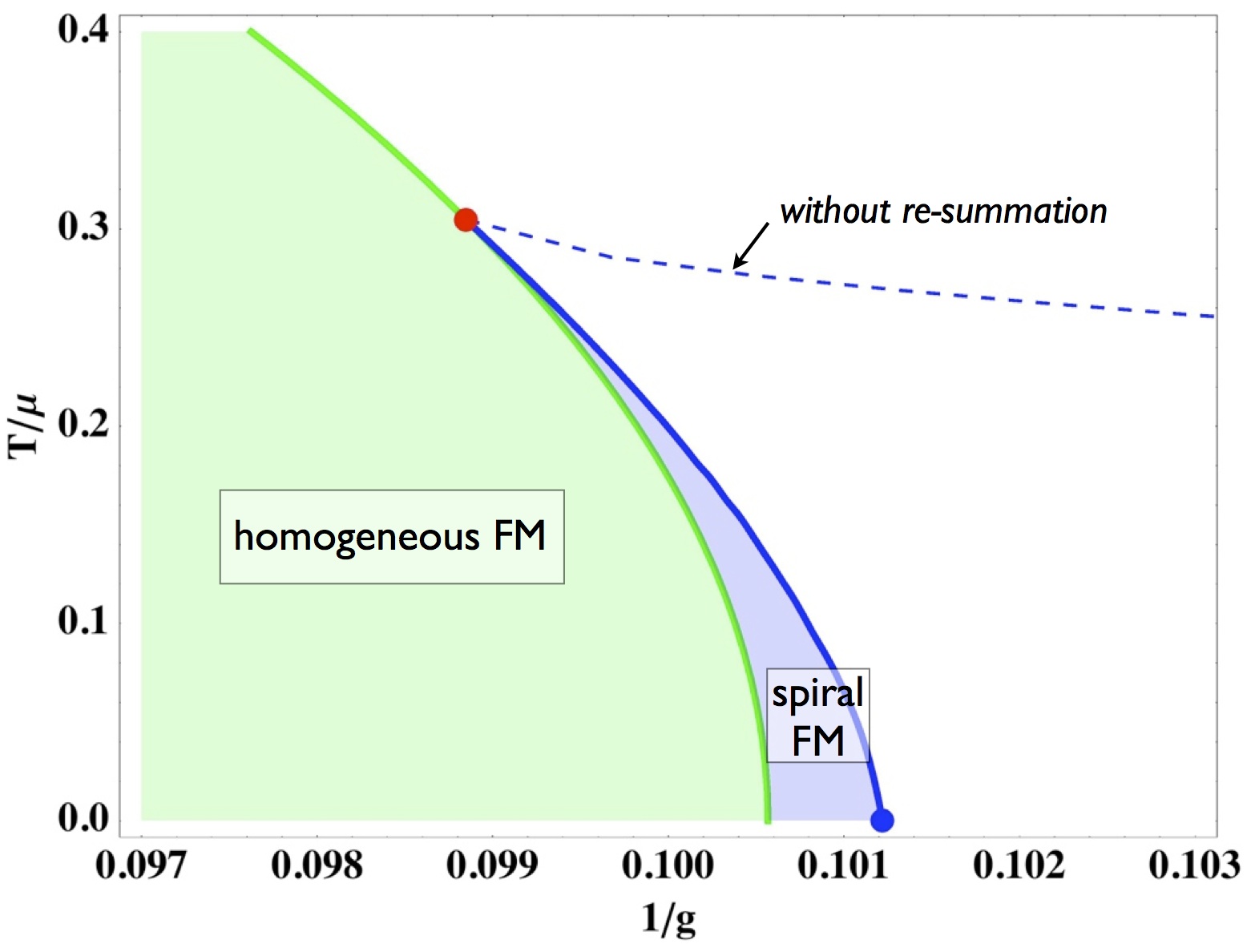
We present a detailed analysis of the non-analytic structure of the free energy for the itinerant ferromagnet near the quantum
critical point in two and three dimensions. We analyze a model of electrons with an isotropic dispersion interacting through a contact
repulsion. A fermionic version of the quantum order-by-disorder mechanism allows us to calculate the free energy as a functional of
the dispersion in the presence of homogeneous and spiralling magnetic order. We re-sum the leading divergent contributions, to derive
an algebraic expression for the non-analytic contribution to free energy from quantum fluctuations. Using a recursion which relates
sub-leading divergences to the leading term, we calculate the full T=0 contribution in d=3. We propose an interpolating functional form,
which allows us to track phase transition lines at temperatures far below the tricritical point and down to T=0. In d=2, quantum
fluctuations are stronger and non-analyticities more severe. Using a similar re-summation approach, we find that despite the different
non-analytic structures, the phase diagrams in two and three dimensions are remarkably similar, exhibiting an incommensurate spiral
phase near to the avoided quantum critical point.
- Breakdown of self-averaging in the Bose glass,
A. Hegg, F. Krüger, and P. Phillips,
Phys. Rev. B 88, 134206 (2013).
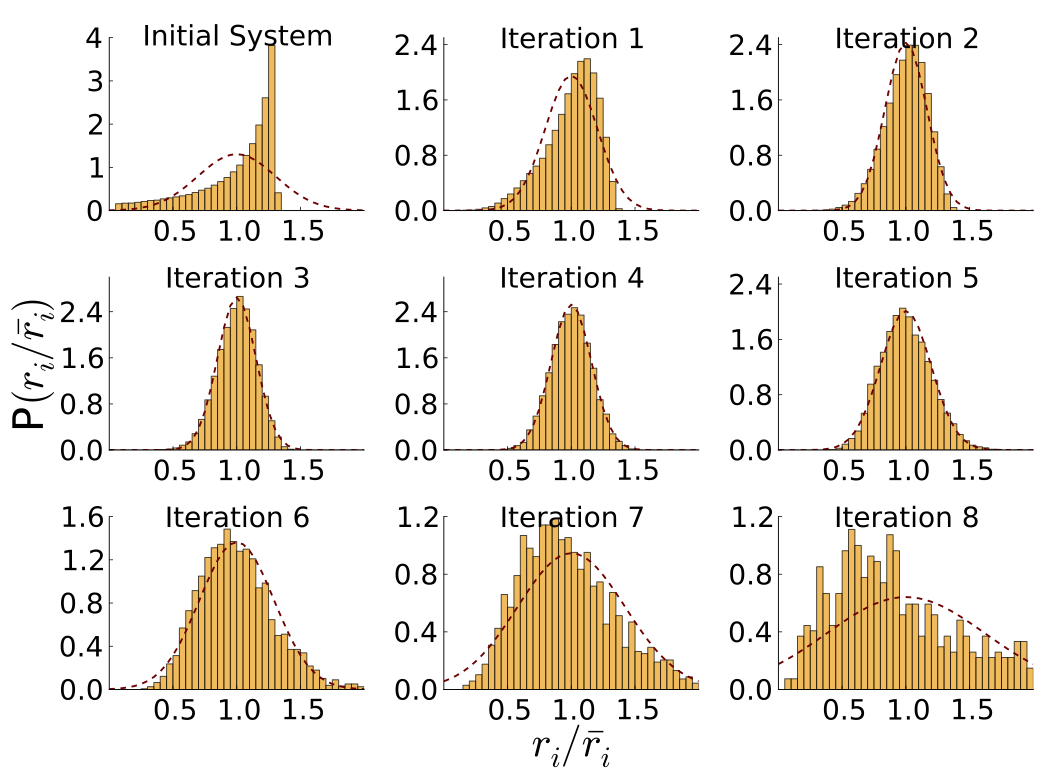
We study the square-lattice Bose-Hubbard model with bounded random on-site energies at zero temperature. Starting from a dual
representation obtained from a strong-coupling expansion around the atomic limit, we employ a real-space block decimation scheme.
This approach is non-perturbative in the disorder and enables us to study the renormalization-group flow of the induced random-mass
distribution. In both insulating phases, the Mott insulator and the Bose glass, the average mass diverges signaling short range
superfluid correlations. The relative variance of the mass distribution distinguishes the two phases, renormalizing to zero in the Mott
insulator and diverging in the Bose glass. Negative mass values in the tail of the distribution signal the presence of rare superfluid
regions in the Bose glass. The breakdown of self-averaging is evidenced by the divergent relative variance and increasingly
non-Gaussian distributions. We determine an explicit phase boundary between the Mott insulator and Bose glass.
- Helical glasses near ferromagnetic quantum criticality,
S. J. Thomson, F. Krüger, and A. G. Green,
Phys. Rev. B 87, 224203 (2013).
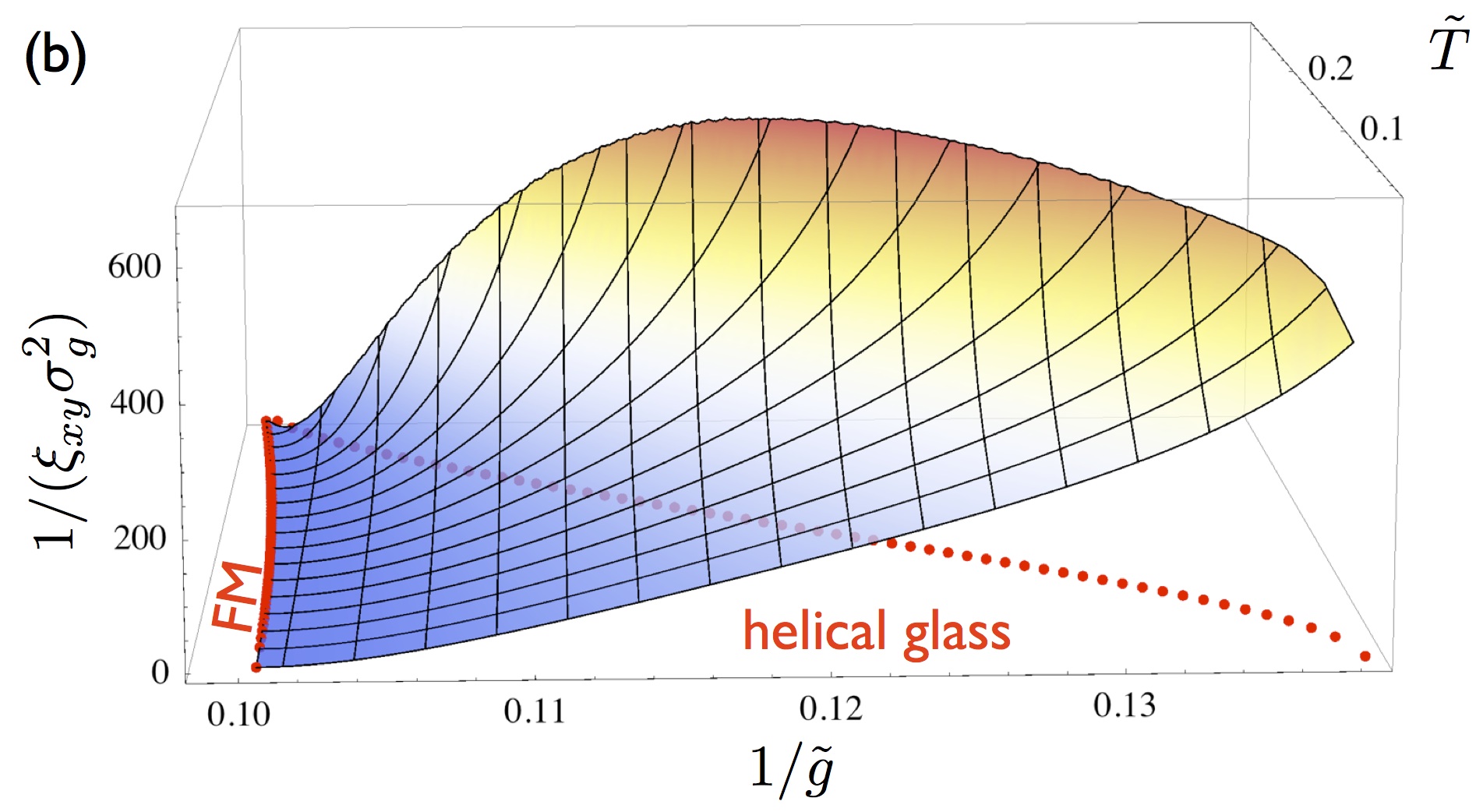
We study the effects of quenched charge disorder on the phase reconstruction near itinerant ferromagnetic quantum critical points in
three spatial dimensions. Combining a replica disorder average with a fermionic version of the quantum-order-by disorder mechanism,
we show that weak disorder destabilizes the ferromagnetic state and enhances the susceptibility towards incommensurate, spiral
magnetic ordering. The Goldstone modes of the spiral phase are governed by a 3d-XY model. The induced disorder in the pitch of the
spiral generates a random anisotropy for the Goldstone modes, inducing vortex lines in the phase of the helical order and rendering
the magnetic correlations short ranged with a strongly anisotropic correlation length.
- Disordered driven coupled cavity arrays: Non-equilibrium stochastic mean-field theory,
G. Kulaitis, F. Krüger, F. Nissen, and J. Keeling,
Phys. Rev. A 87, 013840 (2013).
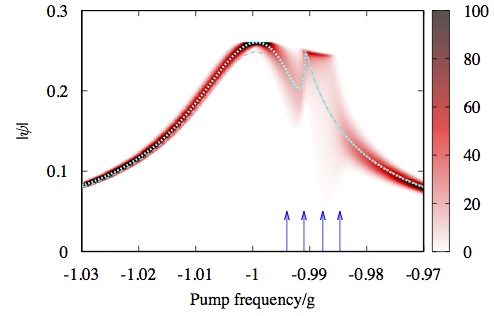
We study the interplay of disorder with pumping and decay in coupled qubit-cavity arrays, the Jaynes-Cummings-Hubbard model. We
find that relatively weak disorder can wash out the bistability present in the clean pumped system, and that moreover, the combination
of disorder in on-site energies and decay can lead to effective phase disorder. To explore these questions, we present a non-equilibrium
generalisation of Stochastic-Mean-Field theory, providing a simple tool to address such questions. This technique is developed for
rather general forms of light-matter coupling, driving, dissipation, and on-site disorder, making it applicable to a wide range of systems.
- Quantum order-by-disorder driven phase reconstruction in the vicinity of ferromagnetic quantum critical points,
U. Karahasanovic, F. Krüger, and A. G. Green,
Phys. Rev. B 85, 165111 (2012).
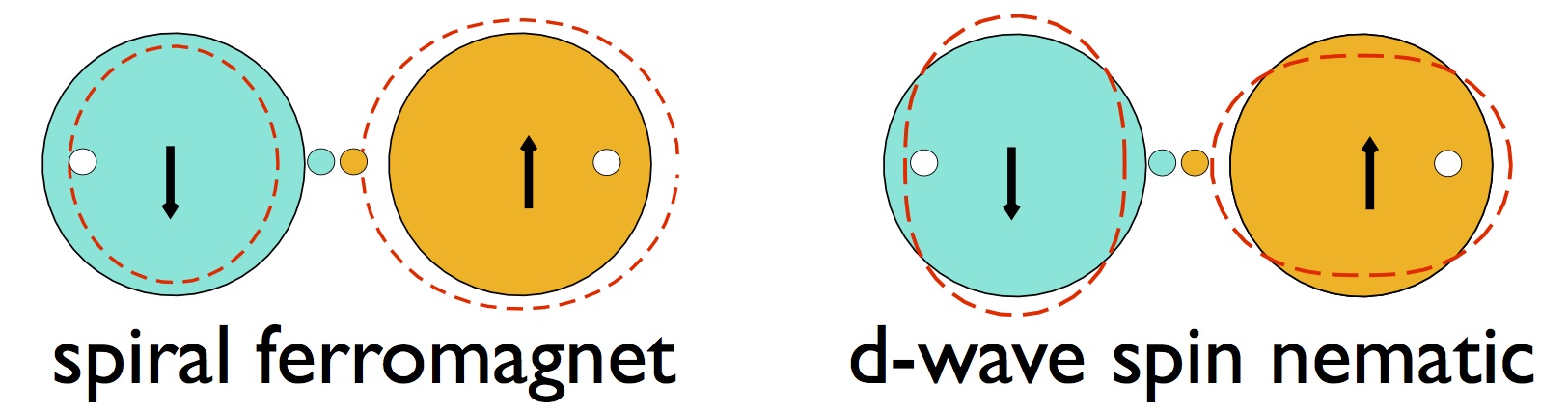
The formation of new phases close to itinerant electron quantum critical points has been observed experimentally in many
compounds. We present a unified analytical model that explains the emergence of new types of order around itinerant ferromagnetic
quantum critical points. The central idea of our analysis is that certain Fermi-surface deformations associated with the onset
of the competing order enhance the phase-space available for low-energy quantum fluctuations and so self-consistently lower
the free energy. We demonstrate that this quantum order-by-disorder mechanism leads to instabilities towards the formation
of spiral and d-wave spin nematic phases close to itinerant ferromagnetic quantum critical points in three spatial dimensions.
- Quantum order-by-disorder near criticality and the secret of partial order in MnSi,
F. Krüger, U. Karahasanovic, and A. G. Green,
Phys. Rev. Lett. 108, 067003 (2012).
The vicinity of quantum phase transitions has proven fertile ground in the search for new quantum phases. We propose a physically
motivated and unifying description of phase reconstruction near metallic quantum-critical points using the idea of quantum
order-by-disorder. Certain deformations of the Fermi surface associated with the onset of competing order enhance the phase
space available for low-energy, particle-hole fluctuations and self-consistently lower the free energy. Applying the notion of quantum
order-by-disorder to the itinerant helimagnet MnSi, we show that near to the quantum critical point, fluctuations lead to an increase
of the spiral ordering wave vector and a reorientation away from the lattice favored directions. The magnetic ordering pattern in this
fluctuation-driven phase is found to be in excellent agreement with the neutron scattering data in the partially ordered phase of MnSi.
- Spin-wave excitations in the ferromagnetic-metallic and in the charge, orbital and spin ordered states
in
Nd(1-x)Sr(x)MnO(3)$ with x~0.5,
H. Ulbrich, F. Krüger, A. A. Nugroho, D. Lamago, Y. Sidis, M. Braden,
Phys. Rev. B 84, 094453 (2011).
Inelastic neutron scattering experiments have been performed on single crystals of Nd(1-x)Sr(x)MnO(3) with x~0.5. Colossal
magnetoresistance (CMR) in the manganites arises from the interplay between a ferromagnetic metallic and antiferromagnetic charge
and orbital ordered insulating state. Therefore, it appears important to compare these phases concerning their underlying magnetic
interaction parameters. Our investigations of the spin-wave disperion in the AFM ordered state of Nd(0.5)Sr(0.5)MnO(3) exhibits a
strongly anisotropic stiffness. The sign of the anisotropy is characteristic for the site-centered model for charge and orbital ordering in
half-doped manganites. Within this model, linear spin-wave theory yields a perfect description of the experimental dispersion.
Furthermore, magnetic excitations in the ferromagnetic metallic state of Nd(1-x)Sr(x)MnO(3) with x=0.49 and x=0.50 exhibit
nearly the same magnon dispersion which can be described with a Heisenberg model including nearest-neighbor interactions.
- Two distinct Mott-Insulator to Bose-glass transitions and breakdown of self averaging in the disordered
Bose-Hubbard model,
F. Krüger, Seungmin Hong, and P. Phillips,
Phys. Rev. B 84, 115118 (2011).
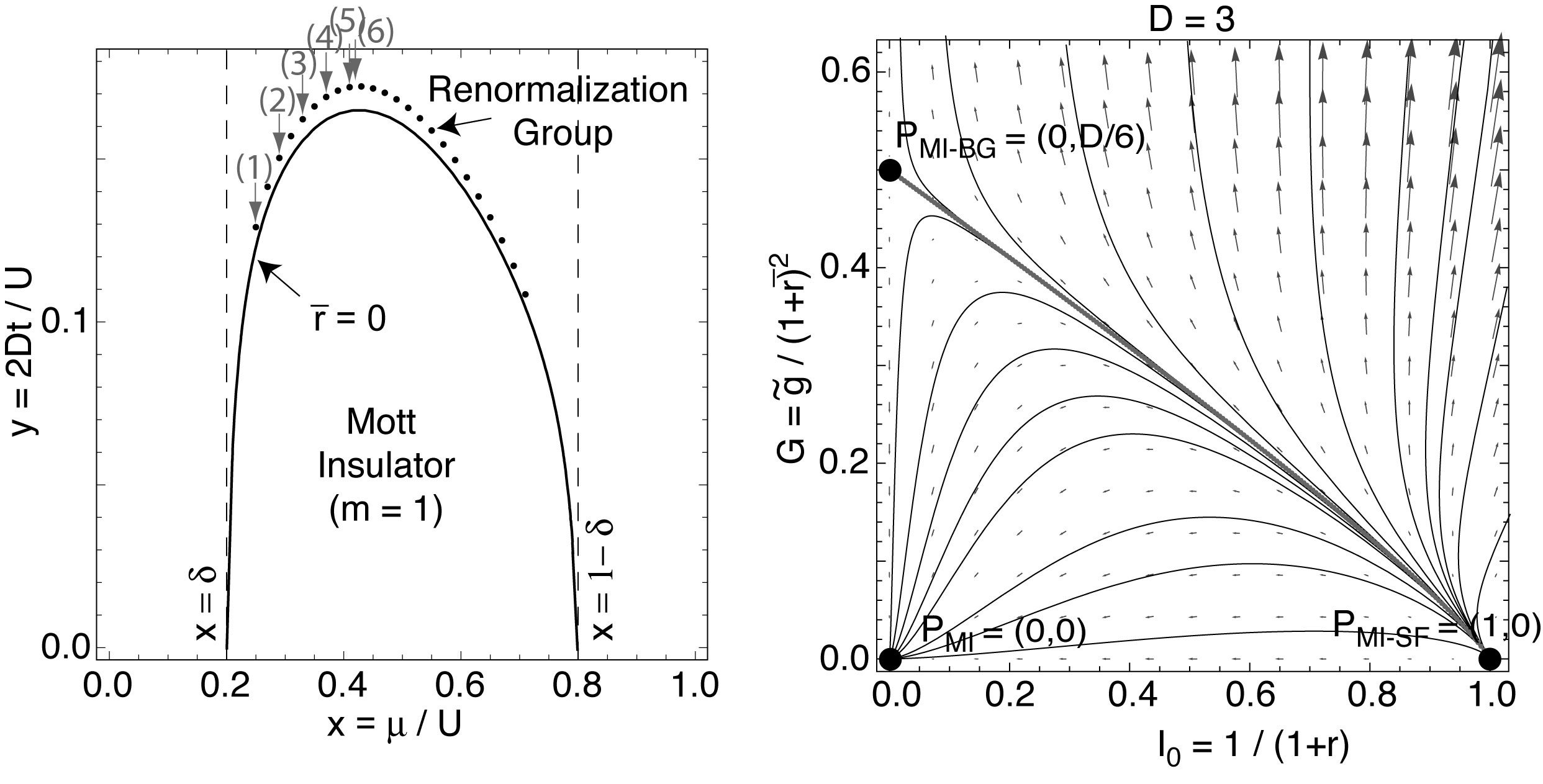
We investigate the instabilities of the Mott-insulating phase of the weakly disordered Bose-Hubbard model within a renormalization group
analysis of the replica field theory obtained by a strong-coupling expansion around the atomic limit. We identify a new order parameter
and associated correlation length scale that is capable of capturing the transition from a state with zero compressibility, the Mott insulator,
to one in which the compressibility is finite, the Bose glass. The order parameter is the relative variance of the disorder-induced mass
distribution. In the Mott insulator, the relative variance renormalizes to zero, whereas it diverges in the Bose glass. The divergence of
the relative variance signals the breakdown of self-averaging. The length scale governing the breakdown of self-averaging is the distance
between rare regions. This length scale is finite in the Bose glass but diverges at the transition to the Mott insulator with an exponent of
$\nu=1/D$ for incommensurate fillings. Likewise, the compressibility vanishes with an exponent of $\gamma=4/D-1$ at the transition. At
commensurate fillings, the transition is controlled by a different fixed point at which both the disorder and interaction vertices are relevant.
- Orbital Ordering and Unfrustrated (pi,0) Magnetism from Degenerate Double Exchange in the Pnictides,
Weicheng Lv, F. Krüger, and P. Phillips,
Phys. Rev. B 82, 045125 (2010).
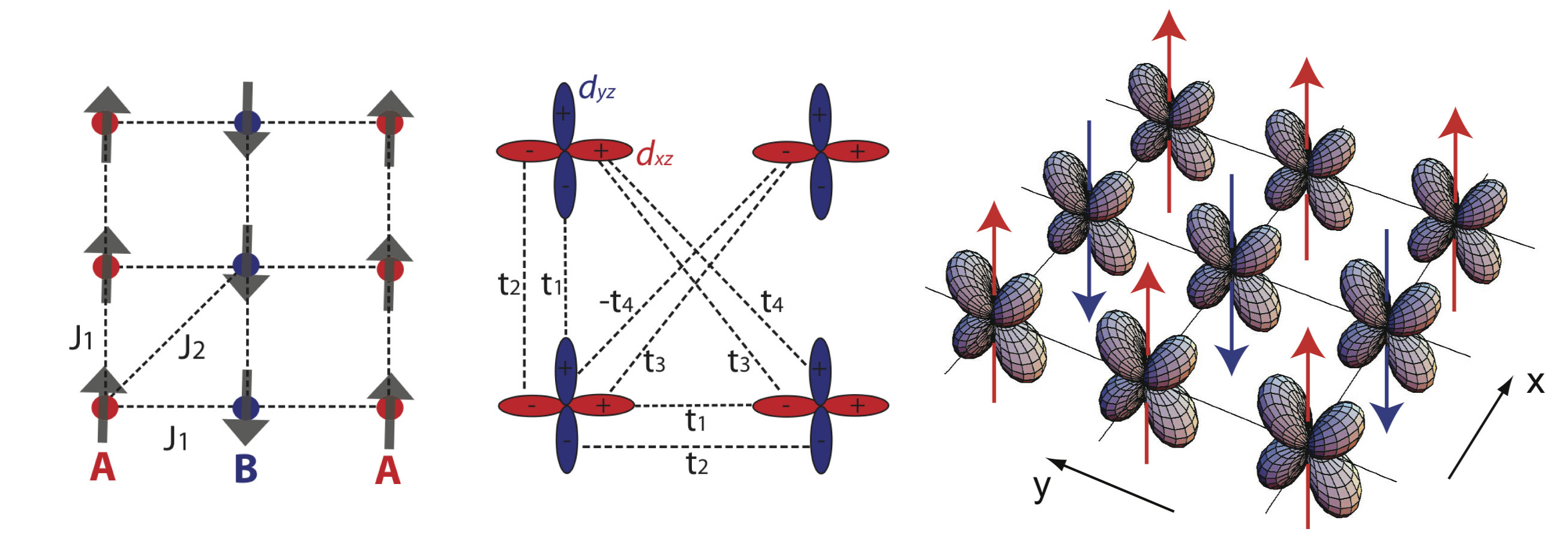
The magnetic excitations of the iron pnictides are explained within a degenerate double-exchange model. The local-moment spins are
coupled by superexchanges J1 and J2 between nearest and next-nearest neighbors, respectively, and interact with the itinerant electrons
of the degenerate d(xz) and d(yz) orbitals via a ferromagnetic Hund exchange. The latter stabilizes (pi,0) stripe antiferromagnetism due to
emergent ferro-orbital order and the resulting kinetic energy gain by hopping preferably along the ferromagnetic spin direction. Taking the
quantum nature of the spins into account, we calculate the magnetic excitation spectra in the presence of both, super- and double-
exchange. A dramatic increase of the spin-wave energies at the competing Néel ordering wave vector is found, in agreement with recent
neutron scattering data. The spectra are fitted to a spin-only model with a strong spatial anisotropy and additional longer ranged couplings
along the ferromagnetic chains. Over a realistic parameter range, the effective couplings along the chains are negative corresponding to
unfrustrated stripe antiferromagnetism.
- Anomalous suppression of the Bose glass at commensurate fillings in the
disordered Bose-Hubbard model,
F. Krüger, Jiansheng Wu, and P. Phillips,
Phys. Rev. B 80, 094526 (2009),
Virtual Journal of Atomic Quantum Fluids 1, (4) (2009).
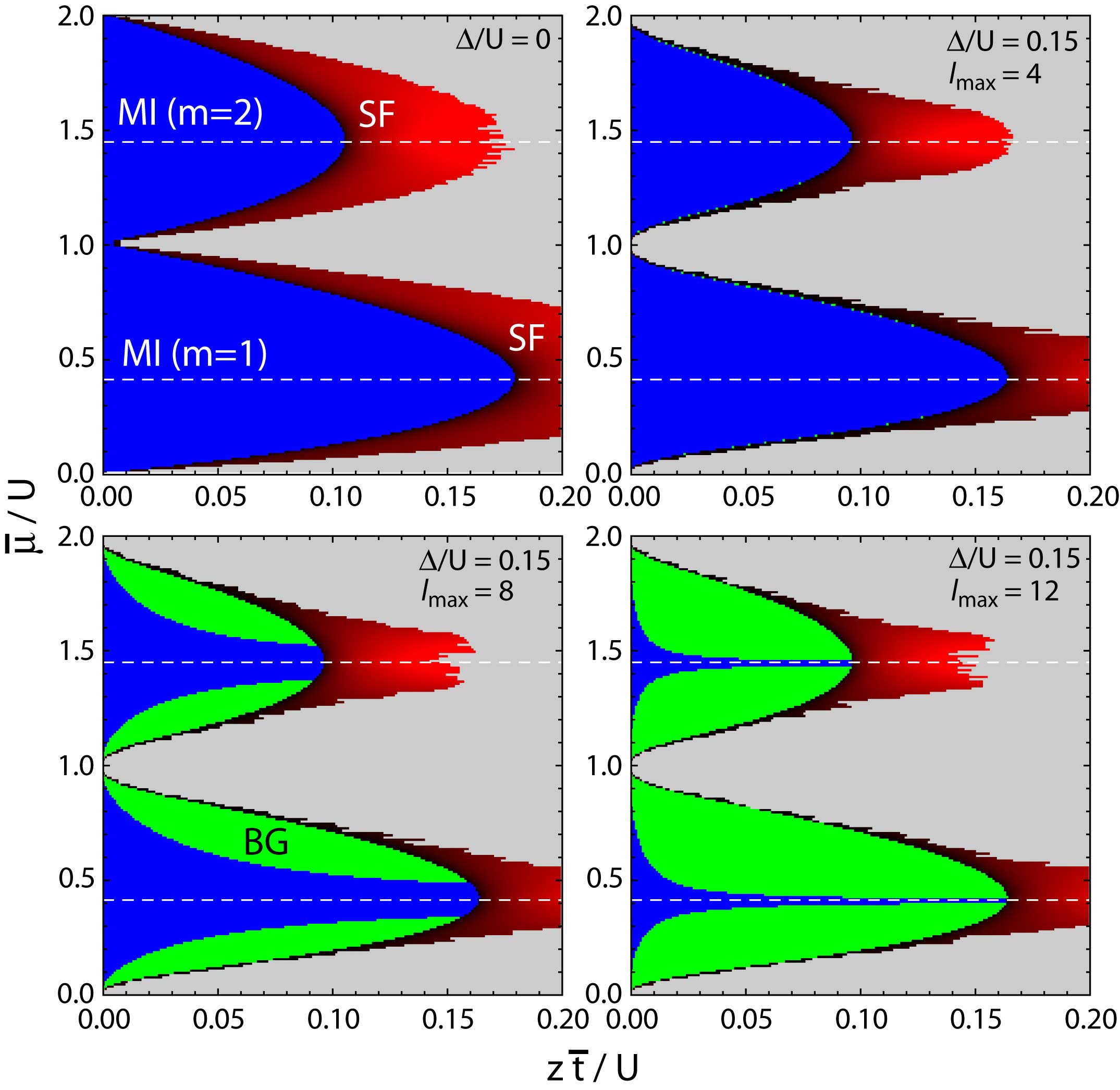
We study the weakly disordered Bose-Hubbard model on a cubic lattice through a one-loop renormalization group analysis of the
corresponding effective field theory which is explicitly derived by combining a strong-coupling expansion with a replica average over
the disorder. The method is applied not only to generic uncorrelated on-site disorder but also to simultaneous hopping disorder
correlated with the differences of adjacent disorder potentials. Such correlations are inherent in fine-grained optical speckle potentials
used as a source of disorder in optical lattice experiments. As a result of strong coupling, the strength of the replica mixing disorder
vertex, responsible for the emergence of a Bose glass, crucially depends on the chemical potential and the Hubbard repulsion and
vanishes to leading order in the disorder at commensurate boson fillings. As a consequence, at such fillings a direct transition
between the Mott-insulator and the superfluid in the presence of disorder cannot be excluded on the basis of a one-loop
calculation. At incommensurate fillings, at a certain length scale, the Mott insulator will eventually become unstable towards
the formation of a Bose glass. Phase diagrams as a function of the microscopic parameters are presented and the finite-size
crossover between the Mott-insulating state and the Bose glass is analyzed.
- Phase diagram of the frustrated, spatially anisotropic S=1
antiferromagnet on a square lattice,
H. C. Jiang, F. Krüger, J. E. Moore, D. N. Sheng, J. Zaanen, and Z. Y. Weng,
Phys. Rev. B 79, 174409 (2009).
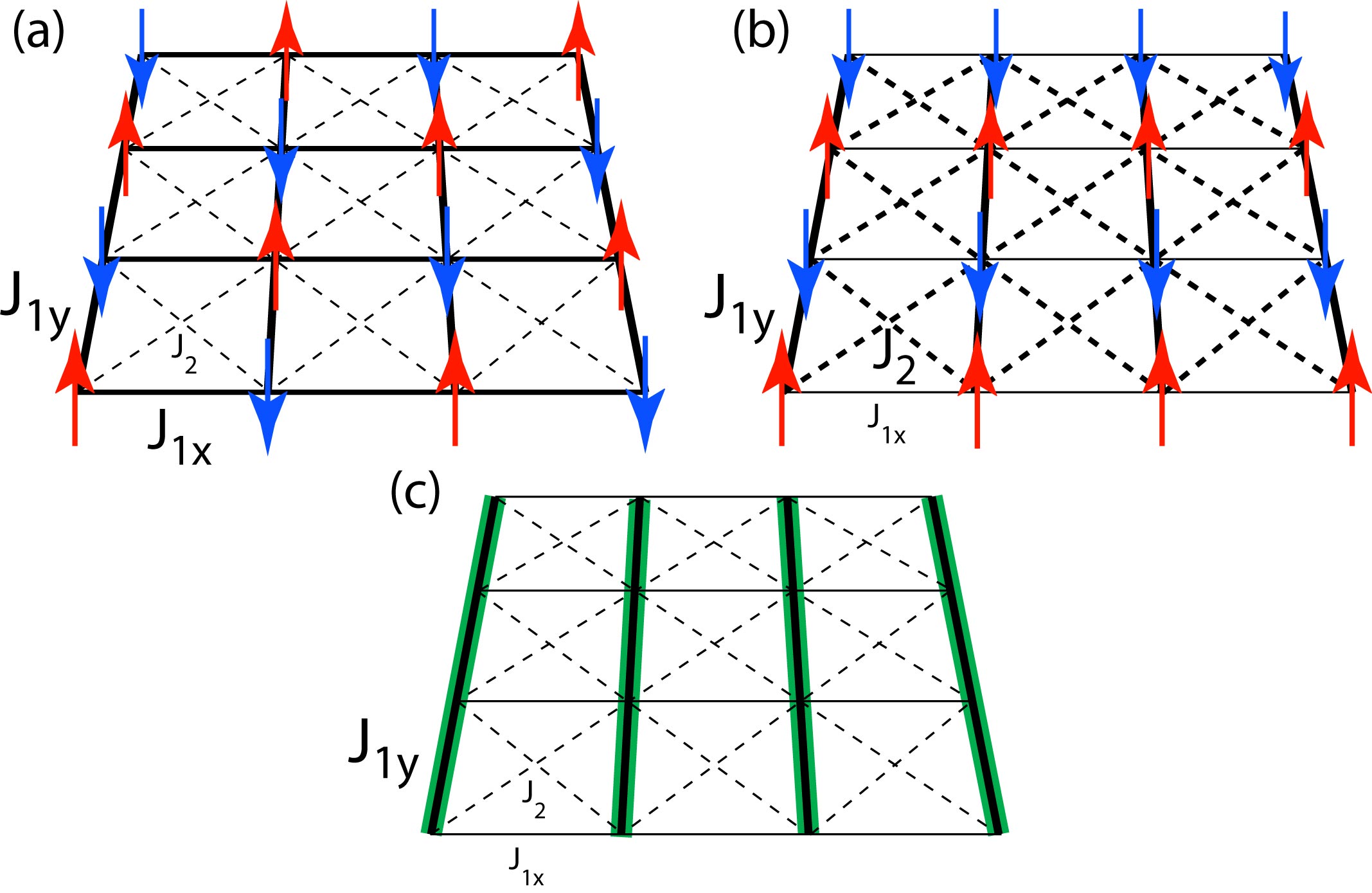
We study the S=1 square lattice Heisenberg antiferromagnet with spatially anisotropic nearest neighbor couplings J1x, J1y
frustrated by a next-nearest neighbor coupling J2 numerically using the density-matrix renormalization group (DMRG) method and
analytically employing the Schwinger-Boson mean-field theory (SBMFT). Up to relatively strong values of the anisotropy, within both
methods we find quantum fluctuations to stabilize the Neel ordered state above the classically stable region. Whereas SBMFT
suggests a fluctuation-induced first order transition between the Néel state and a stripe antiferromagnet for 1/3<J1x/J1y<1
and an intermediate paramagnetic region opening only for very strong anisotropy, the DMRG results clearly demonstrate that the two
magnetically ordered phases are separated by a quantum disordered region for all values of the anisotropy with the remarkable implication
that the quantum paramagnetic phase of the spatially isotropic J1-J2 model is continuously connected to the limit of decoupled
Haldane spin chains. Our findings indicate that for S=1 quantum fluctuations in strongly frustrated antiferromagnets are crucial and
not correctly treated on the semiclassical level.
- Spin-orbital frustrations and anomalous metallic state in iron-pnictide superconductors,
F. Krüger, S. Kumar, J. Zaanen, and J. van den Brink,
Phys. Rev. B 79, 054504 (2009),
Virtual Journal of Applications of Superconductivity 16, (4) (2009).
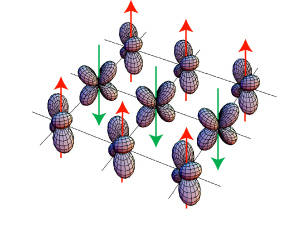
We develop an understanding of the anomalous metal state of the parent compounds of recently discovered iron based superconductors
starting from a strong coupling viewpoint, including orbital degrees of freedom. On the basis of an intermediate-spin (S=1) state for the
Fe(2+) ions, we derive a Kugel-Khomskii spin-orbital Hamiltonian for the active t(2g) orbitals. It turns out to be a highly complex
model with frustrated spin and orbital interactions. We compute its classical phase diagrams and provide an understanding for the stability
of the various phases by investigating its spin-only and orbital-only limits. The experimentally observed spin-stripe state is found to be
stable over a wide regime of physical parameters and can be accompanied by three different types of orbital orders. Of these the orbital-
ferro and orbital-stripe orders are particularly interesting since they break the in-plane lattice symmetry --a robust feature of the undoped
compounds. We compute the magnetic excitation spectra for the effective spin Hamiltonian, observing a strong reduction of the ordered
moment, and point out that the proposed orbital ordering pattern can be measured in resonant X-ray diffraction.
- Fermionic quantum criticality and the fractal nodal surface,
F. Krüger and J. Zaanen,
Phys. Rev. B 78, 035104 (2008).

The complete lack of theoretical understanding of the quantum critical states found in the heavy fermion metals and the normal states
of the high-Tc superconductors is routed in deep fundamental problem of condensed matter physics: the infamous minus signs
associated with Fermi-Dirac statistics render the path integral non-probabilistic and do not allow to establish a connection with critical
phenomena in classical systems. Using Ceperley's constrained path-integral formalism we demonstrate that the workings of scale
invariance and Fermi-Dirac statistics can be reconciled. The latter is self-consistently translated into a geometrical constraint structure.
We prove that this "nodal hypersurface" encodes the scales of the Fermi liquid and turns fractal when the system becomes quantum
critical. To illustrate this we calculate nodal surfaces and electron momentum distributions of Feynman backflow wave functions and indeed
find that with increasing backflow strength the quasiparticle mass gradually increases, to diverge when the nodal structure becomes fractal.
Such a collapse of a Fermi liquid at a critical point has been observed in the heavy-fermion intermetallics in a spectacular fashion.

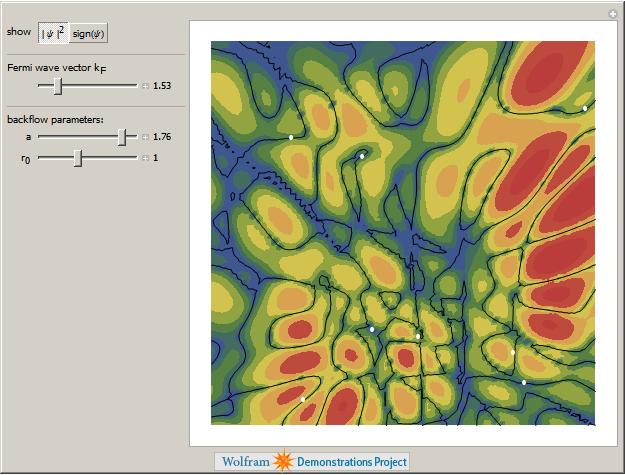 Triggered by our paper, the visualization of nodal surfaces of backflow
Triggered by our paper, the visualization of nodal surfaces of backflow
wavefunctions has been implemented as a
MATHEMATICA demonstration project.
 Synopsis: "Fractals and quantum criticality" by Sarma Kancharla
Synopsis: "Fractals and quantum criticality" by Sarma Kancharla
- Pacifying the Fermi-liquid: battling the devious fermion signs,
J. Zaanen, F. Krüger, J.-H. She, D. Sadri, S. I. Mukhin,
Iranian Journal of Physics Research, Vol. 8, No. 2, 39 (2008).
The fermion sign problem is studied in the path integral formalism. The standard picture of Fermi liquids is first critically analyzed, pointing
out some of its rather peculiar properties. The insightful work of Ceperley in constructing fermionic path integrals in terms of constrained
worldlines is then reviewed. In this representation, the minus signs associated with Fermi-Dirac statistics are self consistently translated
into a geometrical constraint structure (the nodal hypersurface) acting on an effective bosonic dynamics. As an illustrative example we use
this formalism to study 1+1-dimensional systems, where statistics are irrelevant, and hence the sign problem can be circumvented. In this
low-dimensional example, the structure of the nodal constraints leads to a lucid picture of the entropic interaction essential to one-
dimensional physics. Working with the path integral in momentum space, we then show that the Fermi gas can be understood by analogy
to a Mott insulator in a harmonic trap. Going back to real space, we discuss the topological properties of the nodal cells, and suggest
a new holographic conjecture relating Fermi liquids in higher dimensions to soft-core bosons in one dimension. We also discuss some
possible connections between mixed Bose/Fermi systems and supersymmetry.
- Magnetic fluctuations in n-type high-Tc superconductors reveal breakdown of fermiology:
Experiments and Fermi-liquid/
RPA calculations,
F. Krüger, S. D. Wilson, L. Shan, S. Li, Y. Huang, H. H. Wen, S. C. Zhang, Pengcheng Dai, J. Zaanen,
Phys. Rev. B 76, 094506 (2007).
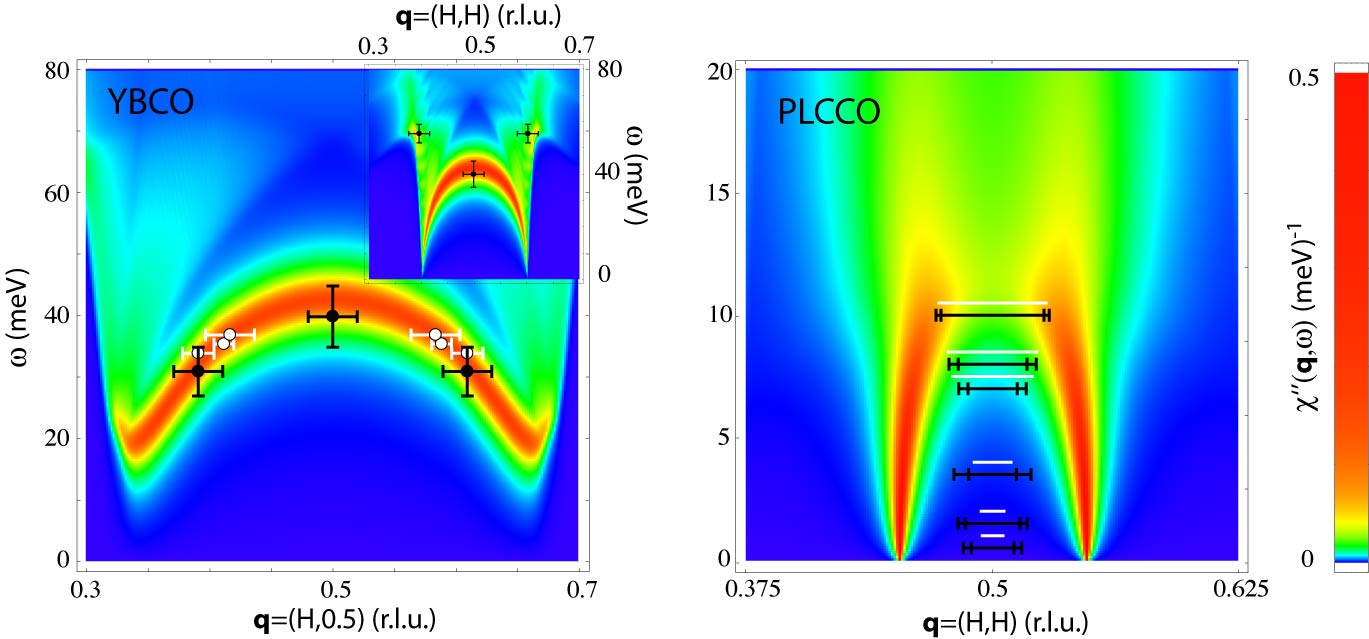
By combining experimental measurements of the quasiparticle and dynamical magnetic properties of optimally electron-doped
Pr(0.88)LaCe(0.12)CuO4 with theoretical calculations we demonstrate that the conventional fermiology approach cannot possibly account
for the magnetic fluctuations in these materials. In particular, we perform tunneling experiments on the very same sample for which a
dynamical magnetic resonance has been reported recently and use photoemission data by others on a similar sample to characterize the
fermionic quasi-particle excitations in great detail. We subsequently use this information to calculate the magnetic response within the
conventional fermiology framework as applied in a large body of work for the hole-doped superconductors to find a profound disagreement
between the theoretical expectations and the measurements: this approach predicts a step-like feature rather than a sharp resonance
peak, it underestimates the intensity of the resonance by an order of magnitude, it suggests an unreasonable temperature dependence
of the resonance, and most severely, it predicts that most of the spectral weight resides in incommensurate wings which are a key
feature of the hole-doped cuprates but have never been observed in the electron-doped counterparts. Our findings strongly suggest that
the magnetic fluctuations reflect the quantum-mechanical competition between antiferromagnetic and superconducting orders.
- Is deconfined quantum criticality in frustrated antiferromagnets ruled out by generic fluctuation induced
first-order behavior?
F. Krüger,
J. Supercond. Nov. Magn. 20, 575 (2007).
Proceeding for International Conference Stripes2006, Rome, Italy.
- Frustrated Heisenberg antiferromagnets:
fluctuation induced first order vs deconfined quantum criticality,
F. Krüger and S. Scheidl,
Europhys. Lett. 74, 896 (2006).
Recently it was argued that quantum phase transitions can be radically different from classical phase transitions with as a highlight the
'deconfined critical points' exhibiting fractionalization of quantum numbers due to Berry phase effects. Such transitions are supposed to
occur in frustrated ('J1-J2') quantum magnets. We have developed a novel renormalization approach for such systems which is
fully respecting the underlying lattice structure. According to our findings, another profound phenomenon is around the corner:
a fluctuation induced (order-out-of-disorder) first order transition. This has to occur for large spin and we conjecture that it is responsible
for the weakly first order behavior recently observed in numerical simulations for frustrated S=1/2 systems.
- Spin-wave dispersion in orbitally ordered La$_{1/2}$Sr$_{3/2}$MnO$_4$,
D. Senff, F. Krüger, S. Scheidl, M. Benomar, Y. Sidis, S. Demmel, and M. Braden,
Phys. Rev. Lett. 96, 257201 (2006).

The magnon dispersion in the charge, orbital and spin ordered phase in La(1/2)Sr(3/2)MnO4 has been studied by means of
inelastic neutron scattering. We find an excellent agreement with a magnetic interaction model basing on the CE-type superstructure.
The magnetic excitations are dominated by ferromagnetic exchange parameters revealing a nearly-one dimensional character at high
energies. The nearest neighbor ferromagnetic interaction in La(1/2)Sr(3/2)MnO4 is significantly larger than the one in the
metallic ferromagnetically ordered manganites. The large ferromagneticinteraction in the charge/orbital ordered phase appears to be
essential for the capability of manganites to switch between metallic and insulating phases.
- The spin excitation spectrum in striped bilayer compounds,
F. Krüger and S. Scheidl,
Phys. Rev. B 70, 064421 (2004),
Virtual Journal of Applications of Superconductivity 7, (5) (2004).
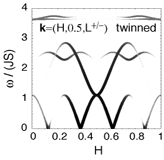
The spin dynamics of bilayer cuprate compounds are studied in a basic model. The magnetic spectral properties are calculated in linear
spin-wave theory for several stripe configurations which differ by the relative location of the stripes in the layers. We focus on the bilayer
splitting of the magnon bands near the incommensurate low energy peaks as well as near the pi resonance, distinguishing between the
odd and even channel. We find that a x-shaped dispersion near the pi resonance is generic for stripes. By comparison of our results to
neutron scattering data for YBa(2)Cu(3)O(6+x) we conclude that the stripe model is consistent with characteristic features of
bilayer high-Tc compounds.
- Spin dynamics of stripes,
F. Krüger and S. Scheidl,
Phys. Rev. B. 67, 134512 (2003).
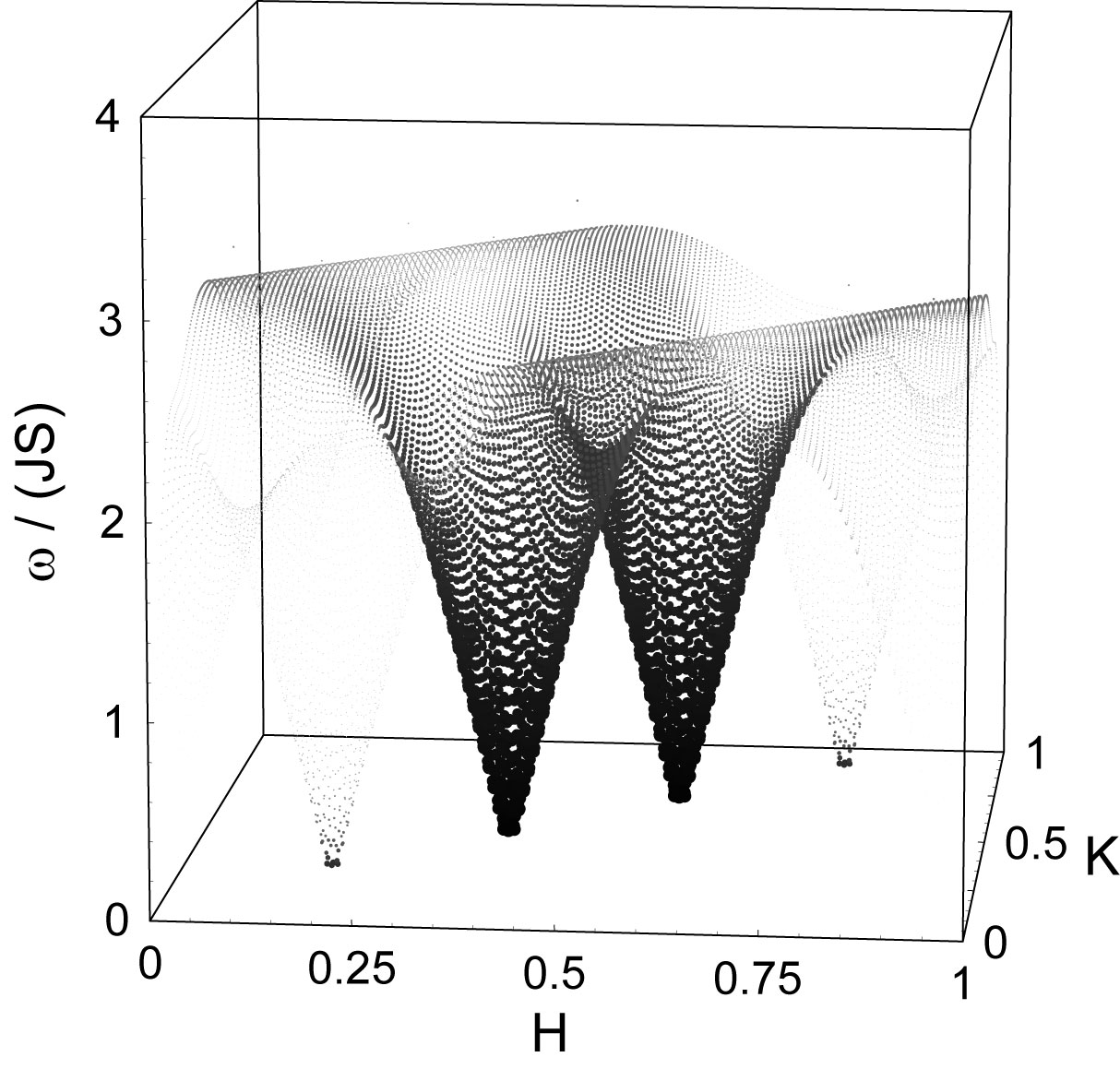
The spin dynamics of stripes in high-temperature superconductors and related compounds is studied in the framework of a spin-wave
theory for a simple spin-only model. The magnon dispersion relation and the magnetic structure factor are calculated for diagonal and
vertical stripes. Acoustical as well as optical bands are included in the analysis. The incommensurability and the pi resonance
appear as complementary features of the band structure at different energy scales. The dependence of spin-wave velocities and
resonance frequencies on the stripe spacing and coupling is calculated. At low doping, the resonance frequency is found to scale
roughly inversely proportional to the stripe spacing. The favorable comparison of the results with experimental data suggests
that the spin-only model provides a suitable and simple basis for calculating and understanding the spin dynamics of stripes.
- Spin and charge ordering transitions in stripes,
F. Krüger and S. Scheidl,
J. Phys. IV France 12, Pr9-259 (2002).
Proceeding for International Workshop on Electronic Crystal (ECRYS), St. Flour, France.
- Non-universal ordering of spin and charge in stripe phases,
F. Krüger and S. Scheidl,
Phys. Rev. Lett. 89, 095701 (2002).
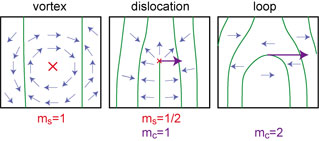
We study the interplay of topological excitations in stripe phases: charge dislocations, charge loops, and spin vortices. In two dimensions
these defects interact logarithmically on large distances. Using a renormalization-group analysis in the Coulomb gas representation of
these defects, we calculate the phase diagram and the critical properties of the transitions. Depending on the interaction parameters,
spin and charge order can disappear at a single transition or in a sequence of two transitions (spin-charge separation). These transitions
are non-universal with continuously varying critical exponents. We also determine the nature of the points where three phases coexist.
- Bond-disordered spin systems:
Theory and application to doped high-$T_\textrm{c}$ compounds,
F. Krüger and S. Scheidl,
Phys. Rev. B 65, 224502 (2002).
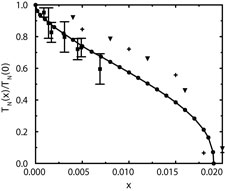
We examine the stability of magnetic order in a classical Heisenberg model with quenched random exchange couplings. This system
represents the spin degrees of freedom in high-Tc compounds with immobile dopants. Starting from a replica representation
of the nonlinear sigma model, we perform a renormalization-group analysis. The importance of cumulants of the disorder distribution
to arbitrarily high orders necessitates a functional renormalization scheme. From the renormalization flow equations we determine the
magnetic correlation length numerically as a function of the impurity concentration and of temperature. From our analysis follows that
two-dimensional layers can be magnetically ordered for arbitrarily strong but sufficiently diluted defects. We further consider the
dimensional crossover in a stack of weakly coupled layers. The resulting phase diagram is compared with experimental data for
La(2-x)Sr(x)CuO(4).