This page is about the physics of the Earth's core.
The core of the Earth accounts for about
30 % of the total mass of our planet, the inner solid core is crystallizing
from the liquid outer core, and the heat released flows to the surface,
driving all the living geological processes of the Earth, including plate
tectonics, volcanism and earthquakes. The cystallization of the inner
core is also responsible for compositional convection in the liquid core,
that is the engine which generates the Earth's magnetic field, shielding
us from the lethal solar wind. So, a sound knowledge of the core is of
fundamental importance, yet, it is one of the most difficult things to
study, and its properties are poorly constrained. For example, we know
that it is mainly made by iron, but it can't be pure iron, because its
density is too low. So it must contain some light element, and the most
likely candidates are sulphur, oxygen, carbon and silicon, but the real
composition of the Earth's core remains one of the major unsolved problems.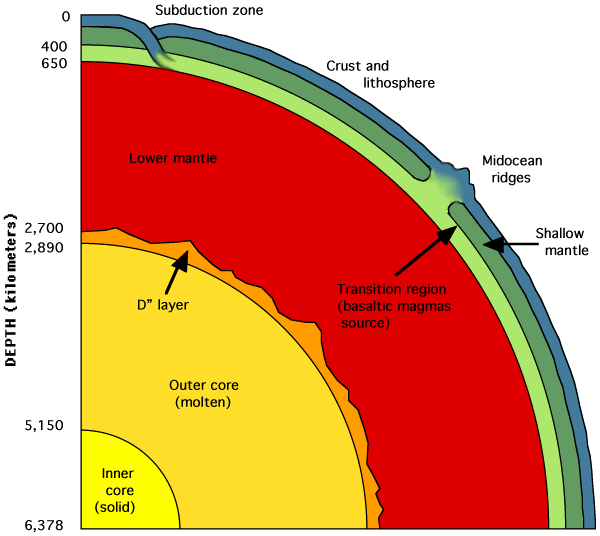 
The
density and the pressure are known quite accurately (within a percent),
but the temperature is unknown, with estimates ranging from 4000 to 8000
K.
We have tackled some of these problems
using first principles techniques, and a report on our
recent work just published in the journal Nature
was picked up by the media, and there were interviews on Channel 4 News
and the Today programme. There was even a half-page item on our work in
the
Daily
Mirror, and on the BBC
on-line web page.
More recently, we participated to the BBC Radio 4 science program "The Material World".
See a recent poster.
The aim of our work is to use ab initio techniques to investigate the properties of liquid and solid iron (both pure and alloyed with light elements) under the conditions of the Earth's deep interior.
Some of the work already done includes:
-
The
viscosity of pure Iron
and Iron-Sulphur
under Earth's core conditions. We have found that the viscosity of liquid
iron is about 13 mPa s, little different from tipical viscosities of liquid
metals under ambient conditions. Sulphur impurities in the concentration
of about 20 % hardly change the properties of the liquid, and the viscosity
in particular is approximatively the same. Initially, the viscosity has
been calculated using the Stokes-Einstein relation, which connects the
viscosity of a liquid with the diffusion coefficient. The latter has been
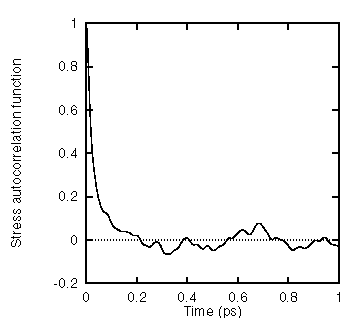
calculated using first-principles molecular dynamics simulations.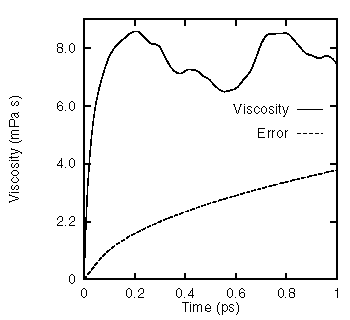 
This
relation is exact when applyed to the diffusion of macroscopic objects,
but it is only approximate when applyed to atoms. However, we have later
calculated the viscosity directly, using the Green-Kubo relation, which
connect the shear viscosity to the integral of the average of the stress
autocorrelation function (see figures on the right). We obtained the value
9 ± 2 mPa s, which is not very far from the one obtained using the
Stokes-Einstein relation, thus confirming its validity.
- Ab-initio investigations of the structural and dynamical properties of Fe, Fe/S and Fe/O under Earth's core conditions.
-
Ab-initio
free-energy
calculations to determine the melting point of iron as a function of pressure,
in the range 50-350 GPa. The condition for two phases to be in thermal
equilibrium at a given temperature T and pressure P is that their Gibbs
free energies G(P,T) are equal. To determine the melting temperature T
at any pressure we calculate G for the solid and liquid phases as a function
of T and determine when they are equal. In fact, we calculate the Helmhotz
free energy F(V,T), and G through its definition G = F + PV. To calculate
the free energy of the liquid we used the techniques called `thermodyanics
integration', starting from a very simple reference system, which is the
sum of inverse power pair-potentials. For the solid, we decompose the free
energy in three parts.
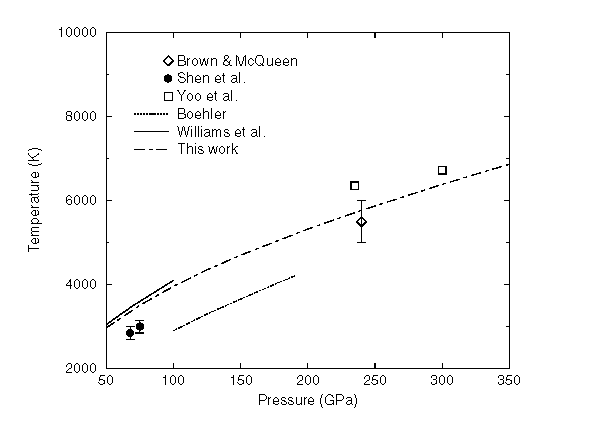The
first is the free energy of the perfect, non-vibrating crystal, which is
straightforward to compute. The second part is the harmonic free energy,
which we calculate by computing the phonon frequencies in the whole Brillouin
zone. The third part is the anharmonic contribution, which we calculate
again using thermodynamics integration. This time the reference system
is a combination of inverse powers and ab initio harmonic. The resulting
melting curve is compared with the experiments here on the right.
- Since we know the free energies we can also calculate the thermodynamics of solid(h.c.p.) and liquid iron.
We have recently used our free energy calculation techniques to put a constraint on the composition and temperature of the Earth's core. Among the possible light elements we consider Sulphur, Silicon and Oxygen.
At Inner Core Boundary solid and liquid are in equilibrium, therefore the chemical potential of all the elements must be equal in the two phases. This fixes the ratio of concentration of the elements in the liquid and in the solid, which in turn fixes the densities. A comparison with seismological data allows us to rule out all binary mixtures, i.e. the Core cannot be made of Fe/S, Fe/Si or Fe/O. The reason is that S and Si do not partition enough between solid and liquid, the concentration in the solid is almost equal to the concentration in the liquid, so the density jump at ICB cannot be reproduced. Oxygen instead partitions too much, very little of it goes into the solid and again the density jump cannot be reproduced.
The composition of the Earth's core must be at least a ternary mixture.
Assuming that the presence of one impurity does not affect the chemical potential of a different element we suggest the following composition for the Earth's core:
Composition at ICB
