6. The sofa challenge

The figure below illustrates the problem of getting an object around a corner between two corridors. We will imagine that the object has extendable length so that at any angle of placement \(\theta\) it just touches the corner and the walls of each corridor.

By calculating the length for each angle we will be able to find the maximum length of object that will fit around the corner.

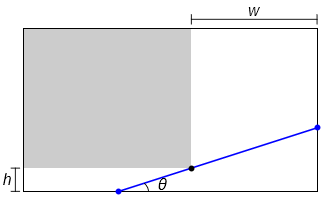
Fig. 6.1 Getting an object around a corner. The object is shown in blue, and the corridor widths have been denoted by \(h\) and \(w\). It is assumed here that the object is very thin, relative to the size of the corridors.

Exercise 6.1

Find an expression for the length of the line \(L\) in terms of \(\theta,h,w\), and use Desmos to plot \(L(\theta)\) for the case when \(h=1\), \(w=3\). Use your result for \(L(\theta)\) to find the longest object that will fit around the corner.