1. Know your limits

Bishop George Berkeley (1685-1753)

And what are these Fluxions? The Velocities of evanescent Increments? And what are these same evanescent Increments? They are neither finite Quantities nor Quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?

In this chapter we introduce the concept of a limit by studying some examples. We do not provide a formal or in-depth treatment of this topic, but by the end of the chapter you should be able to:

• use correct mathematical notation and language to describe a limit

• deal with ratios of infinitesimally small or large quantities

• avoid misconceptions involving “a difference of infinities”

1.1. Informal concept

We have already seen that there are times when we may want to describe the behaviour of a function as its argument approaches a value without actually being equal to it. This is the idea that lies behind the mathematical definition of a limit.

By way of example, let us consider one of the functions that we looked at previously:

(1.1)\[y=\frac{3x^2+2x}{1-2x}.\]

We have looked at the behaviour of this fraction as \(x\) approaches (“tends to”) the value of 1/2 [see asymptotes-03]. The result is different as we approach from either the left or the right side of the \(x\)-axis, which we may denote mathematically by writing:

(1.2)\[\begin{split}\begin{align*} \lim_{x\rightarrow \left(\frac{1}{2}\right)^{-}}y=+\infty\\ \lim_{x\rightarrow \left(\frac{1}{2}\right)^{+}}y=-\infty \end{align*}\end{split}\]

The expressions state that “in the limit” as \(x\) tends to \(\frac{1}{2}\),

• from the left, \(y\) tends to positive infinity

• from the right, \(y\) tends to negative infinity

These are one-sided limits. Since the left- and right- sided limits are not the same, we cannot meaningfully speak of the limit as \(x\) tends to \(\frac{1}{2}\) without specifying the direction, as indicated by the superscript \(+/-\) used in (1.2).

For comparison, consider the function \(1/x^2\). As \(x\) tends to zero the left- and right- sided limits of this function are both positive infinity and so we can simply say:

(1.3)\[\begin{equation} \lim_{x\rightarrow 0}\frac{1}{x^2} = \infty. \end{equation}\]

Exercise 1.1

What do you think is the correct result for:

\[\begin{equation*} \lim_{x \to \infty} ( x^2 - x ) \ ? \end{equation*}\]

Solution

When considering the limiting difference between two arbitrarily large quantities, we need to be very careful.

In this example the limit appears to “go like” \(\infty - \infty\), so you would be forgiven for thinking the result is zero. On the other hand, there is a sense in which \(x^2\) is “much bigger” than \(x\).

Indeed, if you try to substitute a large value of \(x\) into the function \((x^2 - x)\) you may correctly infer that the function can get arbitrarily large by making \(x\) sufficiently large. So this limit appears to be infinity. This can be demonstrated by factorisation:

\[\begin{equation*} (x^2 - x) = x (x-1) \end{equation*}\]

Both parts of the factorised expression approach infinity, which demonstrates that the limit is positive infinity.

1.2. Finite limits

The limits in the examples above are infinite, but it doesn’t have to be that way. In horiz-ass we saw an example with a horizontal asymptote:

\[\begin{equation*} \lim_{x\to\infty}\frac{x^2+3x+1}{(2x-3)(2x+3)}=\frac{1}{4}. \end{equation*}\]

Although both the numerator and denominator here can get arbitrarily large, they do so at a similar rate (like \(x^2/4x^2\)) and so their ratio remains finite.

Exercise 1.2

Determine the following limit:

\[\begin{equation*} \lim_{x\to \infty}\frac{\sqrt{x^2 + 2} }{3 x} \end{equation*}\]

Solution

Using the technique of dividing both parts of the fraction by the largest power of \(x\) in the denominator:

\[\begin{equation*} \lim_{x\to \infty}\frac{\sqrt{x^2 + 2} }{3 x} = \lim_{x\to \infty}\frac{\sqrt{1 +\frac{2}{x^2}}}{3} =\frac{\sqrt{1+0}}{3}=\frac{1}{3}\ . \end{equation*}\]

Exercise 1.3

Find the following limits:

(a) \(\qquad \displaystyle\lim_{x\to\infty} \frac{x+2}{x^2-2}, \qquad \qquad \) (b) \(\lim_{x\to\infty} \frac{x-2}{x+2}\).

Solution to (a)

\(\displaystyle\lim_{x \to \infty}\frac{x+2}{x^2 - 2} = \lim_{x \to \infty} \frac{1/x + 2/x^2}{1-2/x^2}= \frac{0+0}{1+0}=0\).

Solution to (b)

\(\displaystyle\lim_{x \to \infty}\frac{x-2}{x+2} = \lim_{x \to \infty} \frac{1 - 2/x}{1+2/x}= \frac{1-0}{1+0}=1\).

In each of the above examples the numerator and the denominator “blow up”, but it is also possible for there to be a finite limit when both parts of a ratio to shrink to zero. For example, consider the following function:

\[\begin{equation*} y=\frac{1-e^{-x}}{x}. \end{equation*}\]

As \(x\to 0\) both the numerator and denominator approach zero, and so the limiting value of their ratio is not obvious. However, a plot of the function can give us a good idea:

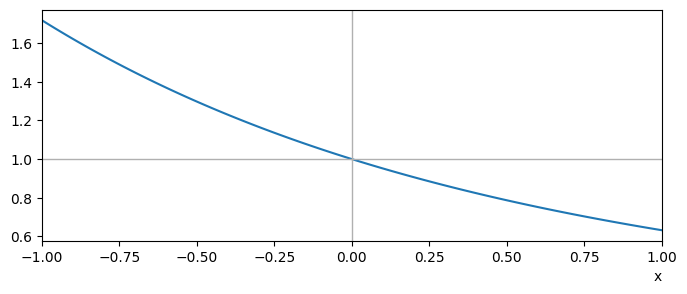
Fig. 1.1 caption

The plot suggests that:

\[\begin{equation*} \lim_{x\rightarrow 0}\frac{1-e^{-x}}{x}=1 \end{equation*}\]

This is possible because whilst both the numerator and denominator tend to zero they do so at exactly the same rate (like \(x/x\)). In the next section we will learn how to find limits of this type.

1.2.1. Limit definition of \(e^x\)

Recall from our earlier work on exponentials that the natural exponent \(e\) satisfies

(1.4)\[\begin{equation} \lim_{\Delta x\rightarrow 0}\frac{e^{\Delta x}-1}{\Delta x}=1 \end{equation}\]

By rearranging this expression we can obtain the following result. This is one of many ways that can be used to define and calculate the exponential function, though it converges quite slowly. Taking \(n=10^7\) gives the value of \(e\) correct to 5 decimal places

(1.5)\[\begin{equation} e = \lim_{\Delta x \rightarrow 0}\left(1+\Delta x\right)^{\frac{1}{\Delta x}} = \lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n. \end{equation}\]

1.3. Do limits always exist?

Not all functions have a limit at all points. For example, consider the square root function \(\sqrt{x}\), which is not real-valued for \(x<0\). This function only has a limit from the right at \(x=0\) and does not have a limit for negative values of \(x\).

A more exotic example is given by the function shown in Fig. 1.2. The function oscillates faster approaching zero and does not approach a particular value, so it does not have a limit as \(x\to 0\).

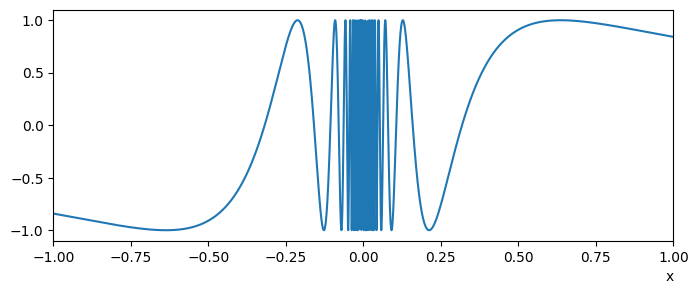
Fig. 1.2 A plot of the function \(\sin(1/x)\).

Exercise 1.4

Do either of the following limits exist?

\[\begin{equation*} \lim_{x\to\infty}\sin(1/x), \qquad \lim_{x\to\infty}\sin(x) \end{equation*}\]

Solution

The first limit exists and is equal to 0.

The second limit does not exist.