The Jacaranda system for process design and optimisation
Table of Contents
Overview of Jacaranda
Jacaranda is a system for process synthesis, or automated process design, intended for conceptual or early stage design. It aims to provide the support necessary for creative and exploratory design, helping the engineer identify the important issues and constraints for a given design problem.

Figure 1: A Jacaranda tree in Rodalquilar, Almería.
Jacaranda has been used for problems in the petrochemical, bioprocessing and brewing industries. Sample problems or case studies in these and other areas are always of great interest to the author!
The aim of Jacaranda is to provide an environment which encourages the engineer to explore the space of solutions available to him or her. Exploration is encouraged through the following features:
- ease of problem definition
- efficiency of implementation, and
- ability to extract information about solution space
Jacaranda aims to provide these features in a portable and efficient system.
Jacaranda is one element, albeit a key one, in my research interests. A full description of the current research in my group is also available.
Licensing
Jacaranda is available, under licence, for use by academic and commercial organizations. If you are interested in acquiring an evaluation licence, instructions and a link to the actual licence can be found here. The evaluation version is available from downloading by following a link in the Jacaranda user's guide.
Process design
One key use of Jacaranda is the design of complete processes. The automated design procedure is based on the use of an implicit enumeration procedure. The problem definition consists of the set of raw materials (feed streams), a list of available processing steps (unit models) and a list of allowable products (which are actually represented by product tank units). The synthesis procedure starts with the raw materials and considers all possible alternative processing steps. The outputs of any processing step are treated in the same way. The procedure therefore is recursive.
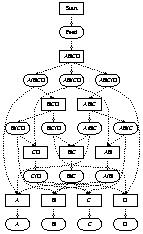
Figure 2: Search graph for Jacaranda automated design procedure
The procedure implicitly generates and traverses a directed graph, as shown in the figure. Using discretisation of all continuous variables in the definition of the design problem, a discrete search space is defined and represented by this search graph. The nodes in the graph correspond to unit model instances and the edges to streams. The source nodes of the graph correspond to feed tanks and the sink nodes are product tanks. Internal nodes are defined by the unit models.
In order to ensure a finite search graph, all continuous quantities in both unit models and streams are mapped to a discrete space. The mapping is defined and controlled by the user of the system although reasonable defaults are provided. For example, a distillation unit may have the operating pressure as one of the design parameters. This pressure will be defined to take on values from a discrete set. Streams are also mapped to discrete space, typically by defining a base amount of each component. This base amount is the smallest amount that will be represented exactly.
For a given objective, the system will generate a list of N-best solutions, for any value of N. Furthermore, the design problem can have multiple objectives. Each objective has its own ranking list generated by the search procedure. The result, therefore, is a set of ranked solutions for each criterion, allowing the engineer to identify elements of the designs which appear in all lists while also gaining insight through a view of the differences between the lists generated.
For instance, the following model, in Jacaranda, will define 4 criteria for ranking solutions:
Criteria environmental # Name Op Model criterion AnnualizedCost sum "capcost/2.5 + opercost - revenue" criterion Sustainability sum "SPI" criterion WaterMass sum "CTWM" criterion Solids sum "SMD" end
Each criterion can be further specified to include the units, the minimum value allowed or expected and the format for printing values of the criterion out. These extra options are not shown in the example above for brevity.
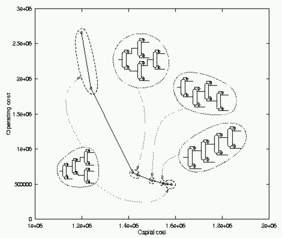
Figure 1: Pareto front for multi-objective optimisation
The figure above shows the Pareto front approximated by Jacaranda for two objectives for a distillation sequence design problem. Along the front, we see different solution structures identified, but are also able to note that the same structure, albeit with radically different operating conditions, is identified for the two extremes of the Pareto front.
Jacaranda provides a hierarchy of classes suitable for use in the synthesis of complete processes and has been used for a variety of problems including distillation sequencing with process heat integration, reaction-separation problems with recycles, oil stabilisation processes and a number of process design problems in biochemical and food engineering including pharmaceutical and biofuel examples.
Heat exchanger network design
Another key area targeted by Jacaranda is the design of heat exchanger networks. A number of targeted procedures have been developed including the use of hybrid optimisation methods. See the highlighted projects on my general research page for more details.
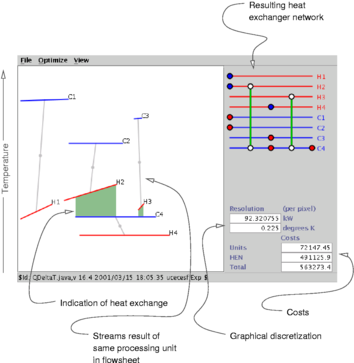
Figure 1: Heat exchanger network design graphical interface
The figure shows the graphical tool in Jacaranda for the design of heat exchanger networks. The graphical interface allows the user to move the lines representing hot and cold streams in two dimensions. Any hot stream, indicated by red in the interface, which overlaps a cold stream, in blue, is a possible integration. The actual network is shown in the top right of the window and optimisation criteria information is displayed on the bottom right.
A screencast (an animated GIF, exactly one minute long, just under 2MB in size) shows how the interface allows an engineer to explore whether better results can be obtained by asking for re-designs of process units (distillation in this example) which would lead to different specifications for the process streams. By increasing the operating pressure of two distillation columns in the example process, a better use of process integration can be achieved, meeting the cooling requirements of two units completely and the heating requirements of one unit. The net annualised cost, including both capital and operating costs of the process units and the heat exchangers, reduces by approximately one quarter.
General modelling environment
The main interface to Jacaranda is through text input files. A specific feature of the text input language is a simple modelling language which allows for the easy customisation of any aspect of Jacaranda. For instance, the following code defines the design model for heat exchangers:
ps.HeatExchanger hex
model
deltain = abs(T1in-T2out) # T1in et al. defined by Jacaranda
deltaout = abs(T1out-T2in)
if abs(deltain - deltaout) < epsilon
lmtd = deltain
else
lmtd = (deltain - deltaout)/log(deltain/deltaout)
endif
A = Q/U/lmtd # Q = duty, U = heat transfer coefficient
capcost = 8600 + 512 * A^0.83
opercost = Cu*Q*h*hpy # Cu = utility cost, hpy = hours per year
end
end
Generic optimisation
Besides the targeted procedures described above for process design, the generic modelling environment provided by Jacaranda implements full support for defining constrained models, both continuous (NLP) and with integer variables (MINLP). The following is an example of a MINLP with a single continuous variable, x, and a single discrete variable, y (Westerlund & Westerlund, 2003).
# Tapio Westerlund & Joakim Westerlund
# GGPECP -- An algorithm for solving non-convex MINLP problems by
# cutting plane and transformation techniques
# Proceedings of ICHEAP-6, Pisa, June 2003.
#
use jacaranda.util.opt
MINLP model
# define the objective function based on continuous variable x
# and discrete (integer) variable y.
f "3*y-5*x"
# define the inequality contraints. this is a set of equations
# where the last expression should evaluate to a vector of
# values. A feasible point is one for which all the values in this
# vector are non-positive.
g
c1 = 2*y + 3*x - 24
c2 = 3*x - 2*y - 8
c3 = 2*y^2 - 2*sqrt(y) + 11*y + 8*x - 39 - 2*sqrt(x)*y^2
{c1, c2, c3}
end
# specify the lower bounds on both the continuous and integer
# optimization variables. Two vectors are expected, the first for
# the continuous (real) variables and the second for the integer
# variables.
a 1 1
# and also specify the upper bounds on these variables
b 6 6
# you can evaluate a specific point by giving a vector of n
# values. If you wish to do so, uncomment the next line:
# evaluate "{1, 1.1}"
print
end
# define an optimizer to see find the optimum
#
# We could use a genetic algorithm. For this case, we define a
# specific population object (and, in principle, can also define a
# chromosome object but the default is suitable for general MINLP
# problems) and then a GA instance which uses this population object.
Population pop
n 20 # population size
crossover 0.7 # crossover rate (70%)
mutation 0.1 # mutation rate (10% -- quite high)
elite 1 # elite set
end
GA ga
output 3 # generate a lot of output
gen 50 # evolve over 50 generations
pfreq 5 # print every 5
function model # the objective function
population pop # the population object
solve # solve the problem
print # and generate some output
end
In general, there may be any number of continuous and discrete variables. Also, the objective function may be a vector, defining multiple criteria for optimisation. A number of solvers are included in Jacaranda: stochastic methods such as genetic algorithms and simulated annealing and direct search methods such as Hooke-Jeeves, Nelder-Meads simplex, implicit filtering from Kelley (1999). Jacaranda implements an interface to Octave which allows models to be written in that language. This interface has only been tested on Linux based systems and is potentially less portable than the Java based components due to its use of network sockets for communication between the Java code and the Octave server.
Further information
A user's guide is available which describes, in detail, how to use Jacaranda and how to write new models for the system. A link for downloading Jacaranda is also available from the user's guide. You can also get extra detailed information and keep up to date with Jacaranda developments by looking at the Jacaranda blog.
Visit my home pages for links to my pages on general research, teaching and other interests.
Software and Hardware compatibility
Jacaranda is written in Java and has been run successfully on a wide range of systems including Linux, Solaris, AIX, and MS Windows. It requires a Java Development Kit or Java Runtime Environment supporting Java version 2, release 1.5 or later.

Figure 1: Photo of a Jacaranda powered yacht in Mallorca (courtesy of A Gavriilidis).