One weakness of using stochastic Lagrangian methods to solve advection-diffusion problems is that the effective resolution is poor where concentrations are low.

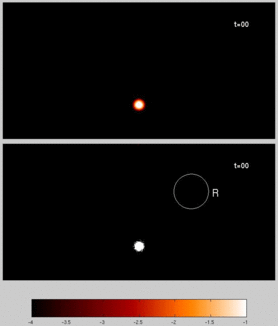
For example, the animation above shows transport in a chaotic advection flow, solved by both an Eulerian (top) and Lagrangian (bottom) method. Notice that almost no particles (out of 10000) reach the measurement region R at t=50. We have been interested in using importance sampling methods to redirect or redistribute particles to find tracer concentrations in pre-specified regions such as R, as accurately as possible.

The animation above shows transport in the same flow, except now using an importance sampling method, based on an algorithm called `go-with-the-winners'. The upper panel shows a quantity, which we have called the `density of trajectories', that theory suggests the particle distribution should follow. The majority of particles now end up in R. Each particle has a weight assigned that allows the concentration in R to be calculated.