Philosophy and Model Theory

Sean Walsh and I wrote a book on philosophy and model theory. Here is a pop-exposition of the very idea of such a book. The book assumes a basic knowledge of formal logic; but this exposition is suitable for non-philosophers and non-mathematicians.
You probably know the game Twenty Questions. Someone thinks of an object, then you have twenty yes/no questions to try to figure out what that object is.
Once you’ve played the game a few times, you might find yourself pondering: Why twenty questions? How many questions do I really need? Ponder that for a bit longer, and you’ll probably end up asking two more precise questions about the game:
- Brain-Teaser A: What’s the smallest number of questions I might ask, and happen to figure out what the object is (whatever it is)?
- Brain-Teaser B: What’s the smallest number of questions I would need to be allowed to ask, to be sure that I can figure out what the object is (whatever it is)?
Brain-Teaser A has a simple answer: One. You might start the game by asking: Are you thinking of Patrick the 88lb wombat? Granted, that would be an odd opening question. Still, if the answer is ‘yes’, well then, you got lucky.
Brain-Teaser B is rather harder. To tackle it, let’s make the setup easier, and suppose that your opponent agrees to choose their object from a pre-agreed list of just 16 objects. In that case, you need only 4 questions to be certain you can figure out which object they chose.
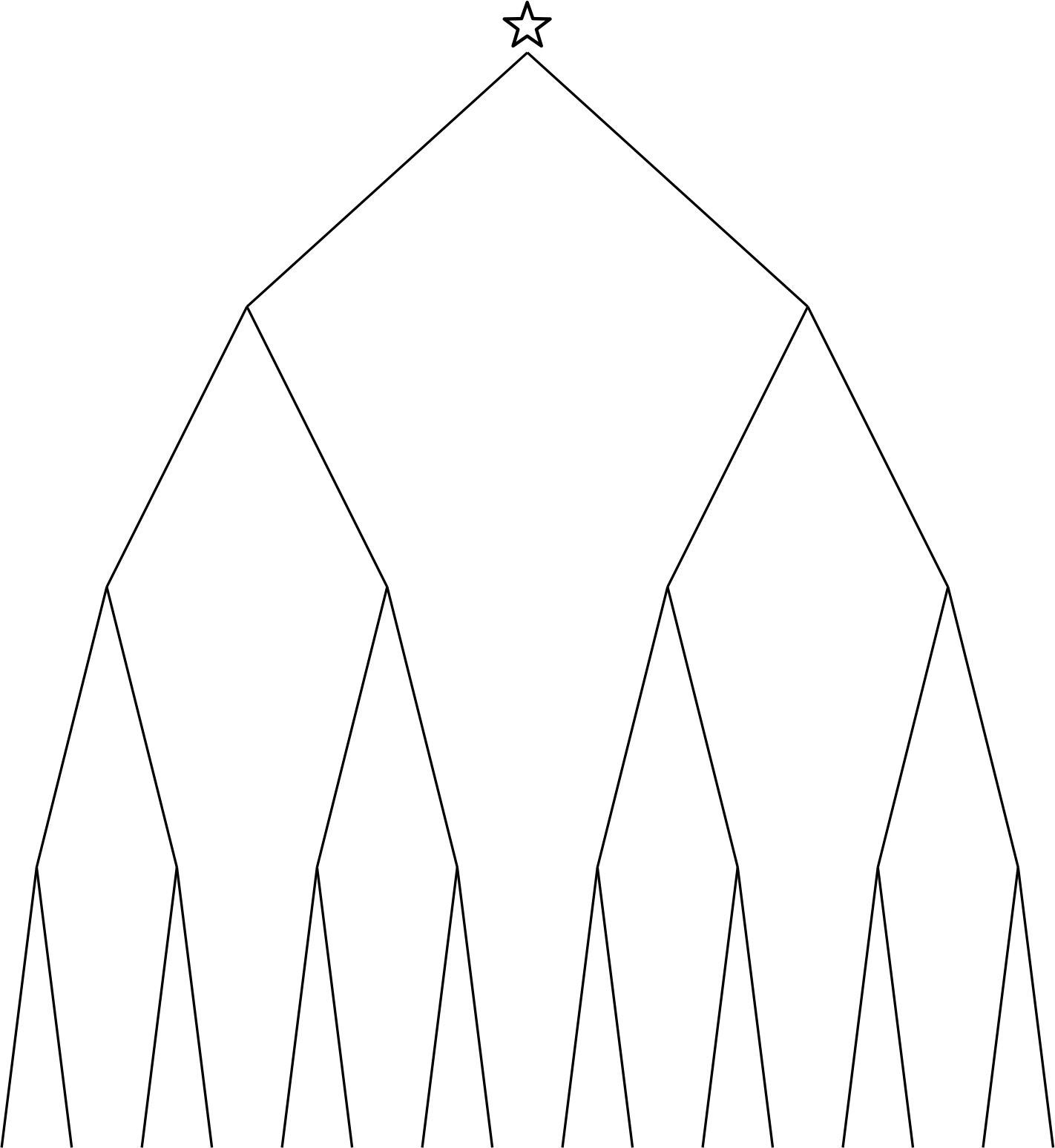
Now let’s think about what happens as we allow your friend to choose from a longer list, and for you to ask more questions. After 20 questions, you have a tree with 220 – i.e. just over a million – paths. So, with 20 questions, you can handle a list with just over a million items on it (provided you choose your questions wisely). More generally, with n questions, you can handle a list with 2n items.
❦
When selecting an object for Twenty Questions, most people choose celebrities, or animals, or landmarks, or whatever. But now imagine that you are playing Twenty Questions against a mathematician, who tells you that she is going to think about some infinite mathematical structure. As usual, your aim is to ask questions, to figure out which structure she has in mind.
What is ‘an infinite mathematical structure’? Well, that’s a system, comprised of infinitely many mathematical objects, related to one another in certain distinctively mathematical ways. For example, the integers (i.e. the positive and negative whole numbers, together with zero) constitute an infinite mathematical structure: there are infinitely many of them, and we can characterise the relations between them in terms of +, ×, and <. Equally, the rationals (i.e. any numbers which can be expressed as a fraction of whole numbers) constitute an infinite mathematical structure. But there are plenty of other structures, such as: the rationals, but without the number ½; a structure which consists of seventeen distinct copies of the integers; or whatever.
Your task, to repeat, is to ask questions and work out which structure your mathematician friend has in mind. How many questions do you need to ask? As in the non-mathematical version of the game, we can break that thought down into two parts.
Start with Brain-Teaser B: What’s the smallest number of questions I would need to be allowed to ask, to be sure that I can figure out what the structure is? Sadly, the answer is: No number of questions can suffice. (Not even some infinite number will do.) There are just too many structures.
Now consider Brain-Teaser A: What’s the smallest number of questions I might ask, and happen to figure out what the structure is? Naïvely, the answer should be: One. After all, you might start the game by asking: are you thinking of the integers? It’s a bold opening move, but, you might just get lucky.
But suppose that your friend tweaks the rules of the game slightly. In the tweaked game, you’re banned from using shorthand phrases like ‘the integers’, or ‘the rationals’. Instead, all of your questions have to be phrased solely in terms of how the elements of the structure relate to one another.
To illustrate: maybe you’ve figured out that the elements of your friend’s structure are arranged as a line. Then you could ask between any two elements, is there always another element? If your friend is thinking of the integers, she’ll have to say ‘no’: there is no whole number between 2 and 3, for example. If she is thinking of the rationals, she’ll have to say ‘yes’: between any p and q, we have the fraction (p+q)⁄2.
This tweak to the rules changes the answer to Brain-Teaser A in a dramatic way. Given the tweak, no matter how lucky you get, no number of questions will allow you to figure out what structure she has in mind. You literally can’t win.
This fact follows from a mathematical result which I’ll revisit below. But it is deeply puzzling. Our game began, even before any questions were asked, with our mathematician friend thinking of some particular structure. We now know that she cannot articulate which structure she has in mind, just by saying how the elements of that structure relate to one another. Well then: How on Earth did she come to think of that particular structure in the first place? Clearly not by articulating how its elements relate to one another; so, how?
❦
Sean Walsh and I recently published a book, Philosophy and Model Theory. The ‘philosophy’ bit should ring a bell; ‘model theory’, perhaps not.
Model theory is a branch of pure mathematics which studies mathematical structures. It has powerful tools for describing such structures. And they also have a precisely defined notion – satisfaction – which they use in place of the intuitive idea that a sentence can be true or false in a structure. (As e.g. the sentence ‘between any two elements, there is another element’ is false in the integers, but true in the rationals.) A structure which satisfies some sentences is also said to be a model of those sentences. Hence the name, model theory.
Back to Twenty Questions. When you phrase your questions in terms of how the elements of the structure relate to one another, the answers you get tell you which sentences are true (or false) in a structure. In the model theorist’s terms, you are learning which sentences the structure satisfies. Now, here is the first deep result of model theory: if some infinite structure satisfies some sentences, so too do infinitely many other different structures. This is known as the Löwenheim–Skolem Theorem. (I can’t prove it here, but one proof involves thinking more about (Christmas) trees, as above.)
This result explains why you can’t win the tweaked version of Twenty Questions. And, more generally, it forces us to confront the question: How could we ever come to think about a particular mathematical structure? (Not by listing what the structure satisfies; so, how?) This is a deep philosophical question associated with model theory. And ultimately – according to Sean and me, at least – it forces us to re-examine the very idea of ‘thinking about a mathematical structure’, and hence to re-examine what it means to engage in mathematical thought.
This is just one of the deep philosophical issues raised by model theory. There are many others. And philosophers routinely employ model theory throughout their work. But, when Sean and I set out to write Philosophy and Model Theory, no one had yet offered a systematic treatment of either the philosophical uses of model theory, or the philosophy of model theory. We have aimed to do both; to trace the dialectical contours of those points where philosophy and model theory meet one another. But we present our book, not as a final word on what philosophically inclined model theorists and model-theoretically inclined philosophers should do. Rather, it’s an invitation to join in.