Strawberry plant propagation algorithm
| Author | Professor Eric S Fraga (e.fraga@ucl.ac.uk) |
| Last revision | 2018-10-19 16:34:25 |
1 Overview and introduction
Below is the code I have written to implement a plant propagation algorithm. It is based on the algorithm Professor Abdellah Salhi and I developed from his original insight into the propagation of strawberry plants. The basis of the code in this particular repository is the code used for the results presented in a paper on the modelling of energy systems for domestic dwellings (Fraga et al., 2015) and in a paper on the control of a dynamic fermentation process (Rodman et al., 2018). This code was in turn based on the code used for the original paper (Salhi & Fraga, 2011). The multi-objective ranking method for fitness evaluation has been described in another publication on renewable energy system design (Fraga & Amusat, 2016).
An implementation of the plant propagation algorithm in the Julia programming language, known as Fresa, is now available and under further development. The advantage of this new implementation is the use of Julia. Julia is a new language for scientific computation which has many key properties including abstract data and dynamic types, multiple dispatch, parallel computing and just-in-time compilation of code for efficiency.
The Strawberry algorithm has been implemented in the Octave programming language. A MATLAB compatible (untested) version, automagically generated from the Octave code, is made available from a link below but it should be noted that the author prefers to use open source software. The Octave version is embedded in the the original org document used to generate this web page. This document has been written using org mode in the Emacs text editor. Org allows for literate programming and uses tangling to generate the actual source files for the code. The code, suitably manipulated to be compatible with MATLAB, can be found here: strawberry-20190624.zip
.
All code (either version) and this document are copyright © 2019, Eric S Fraga, all rights reserved. Permission is given to use this code for evaluation purposes. The code is made available with no warranty or guarantee of any kind. Use at own risk. The code from the above link includes some supplementary functions are required for the Strawberry method (utility functions, multi-objective genetic algorithm (MOGA), and multi-objective steepest descent (MOSD)).
Please let the author know if you download the code. Further, if the Strawberry code is used, please do let the authors know and the above publications must be cited in any research papers written. Feedback, including bug reports for either Octave or MATLAB distribution, is most welcome.
In the following code, we assume column vectors for decision variables and objectives. The convention on constraint violation a positive value for infeasible solutions and non-positive for feasible.
2 Version information
Major version log:
- May 2018
neighbourandrandom solutionfunctions have been refactored to include the lower and upper bounds as arguments. This will affect any codes that defined their own such functions.- November 2016
- change of interface to Strawberry: the objective function must now return not only the objective function values (first entry in return list) but also the feasibility (measure of constraint violation) of the point in the search space (as second entry).
- July 2016
- multi-objective version extended to work for any number of criteria instead of just 2.
- October 2015
- started work on a MI-Strawberry version, hopefully as upwards compatible as possible.
- September 2015
- implemented a rank based fitness, used to prepare results in the paper on understanding the impacts of constraints. There is now a choice of fitness functions as the old, Pareto based, fitness function is still available (cf. Deb (2000) for an example).
3 Strawberry – main entry point
3.1 overview
The algorithm is evolutionary, iterating over a number of generations. In each generation, the solutions are ranked according to the objective function values. In each generation, a number are selected for propagation. Each solution can propagate itself a number of times and a certain distance with both aspects being a function of the solution's fitness. The best solutions propagate more but for shorter distances to exploit the quality of the solution, i.e. a local search; the not so good solutions propagate less but further to explore the domain, i.e. a global search.
A hybrid procedure using a multi-objective steepest descent method, MOSD, is optional.
All of the following src blocks will be tangled to the same strawberry.m file.
The default distance and neighbour functions are suitable for using Strawberry to solve this problem:
![\begin{align*}
&& \min_{x\in\cal{D}} z & = f(x) \\
\mbox{where} && \cal{D} & \equiv [a,b]^n \subset {\cal{R}}^{n} \\
\mbox{subject to} && g(x) & \le 0
\end{align*}](ltxpng/strawberry_29e7741a19b8585f472ed637bf36a1f747130c60.png)
3.2 function definition
function [x z nf ninf bestgen] = strawberry(x0, a, b, f, ngen, npop, nrmax, ns, population_strategy, output)
3.2.1 Arguments
The function has the following arguments:
- x0
- initial member of the population of solutions
- a
- lower bounds on all variables
- b
- upper bounds for all variables
- f
- handle for the objective function which has signature
[z g] = f(x)
where
zis a vector of objective function values andgindicates whether a solution is feasible (g <= 0)or infeasible (g > 0). The actual value ofgfor infeasible solutions is used to rank solutions. Negative values ofgare not used at all. If your objective function is unconstrained, simply ensure that0is returned as the second entry in the return list. - ngen
- one of the stopping criteria: maximum number of generations of plant propagation to allow
- npop
- the base number in the population. The actual number will be larger, depending on the value of
nrmax.npopdecides how many plants actually propagate but the number of new solutions depends on the fitness of those chosen to propagate and the maximum number of runners allowed,nrmax. - nrmax
- the maximum number of runners to create for any solution if chosen to propagate.
- ns
- a stopping criterion based on the number of consecutive generations for which no new best solution is found.
- population_strategy
- The strategy to use for creating a new population after the propagation of chosen solutions:
The strategy to use for creating a new population after the propagation of chosen solutions:
- newly created solutions (propagated) alone
- newly created solutions along with those selected for propagation
- the best from the current population, where best will be a single solution for single objective optimisation and a set of non-dominated solutions for multi-objective optimisation.
- union of the best, the selected and the new solutions.
- output
- An integer indicating how often to output statistics about the search.
In all of the above, vectors (solutions and objective function values for multi-objective optimisation) are column vectors.
Only the first four arguments, x0, a, b and f, are required. The rest are optional and default to the following values:
| ngen | 1000 |
| npop | 100 |
| nrmax | 5 |
| ns | 100 |
| population_strategy | 4 |
| output | ngen/50 |
3.2.2 Return values
The function returns the best point found, x, with associated objective function values, z. It also returns information on the search:
-
nf - number of objective function evaluations.
-
ninf - number of infeasible function evaluations.
-
bestgen - the generation in which the best solution,
<x,z>, was obtained.
For multi-objective optimisation, x and z will be an approximation to the Pareto front defined by a set of non-dominated points and associated objective function values.
3.3 initialisation
global esfdebug global mosd_numberimproved global npruned global nsimilar global strawberry_archive global strawberry_fitness_method global strawberry_diversity_tolerance global strawberry_neighbourfn global strawberry_octave global strawberry_output_population mosd_numberimproved = 0; npruned = 0; nsimilar = 0; stderr = 2; # for MATLAB compatibility warning ('error', 'Octave:broadcast'); ## process arguments if nargin<9, population_strategy = 4; end # population selection strategy if nargin<8, ns = 100; end # number of stable generations if nargin<7, nrmax = 5; end # number of runners if nargin<6, npop = 100; end # population size if nargin<5, ngen = 1000; end # number of generations if nargin<4 disp('Error: need at least 4 arguments to Strawberry method: x0, a, b & f.') return end if nargin<10, output = ngen/50; end # how often to output status of population ## process global variables if isempty (strawberry_archive) strawberry_archive = 0; endif if strawberry_archive > 0 printf(': pareto solutions are archived\n'); endif if isempty (strawberry_fitness_method) strawberry_fitness_method = 1; #choose MOGA fitness for now end strawberry_diversity_tolerance = norm(b-a) / 1000; ## determine the number of processors to use in parallel. If the ## variable has not been set, we use the system function to determine ## how many processors there are global strawberry_numberofprocessors if isempty(strawberry_numberofprocessors) strawberry_numberofprocessors = 1 # not currently working for np>1, nproc(); endif if strawberry_numberofprocessors > 1 printf (': using %d processors for parallel processing.\n', strawberry_numberofprocessors); else printf (': not using any parallel processing on a single processor system.\n'); endif if strawberry_octave if strawberry_numberofprocessors > 1 starttime = time; # use wall clock time instead of CPU time else starttime = cputime; endif else tic; # start wall clock timer starttime = 0; # for later use in output statistics endif if isempty(strawberry_output_population) strawberry_output_population = 0 endif strawberry_initialise printf(': ngen=%d npop=%d nrmax=%d ns=%d population strategy=%d and tolerance=%f fitness method=%d\n', ngen, npop, nrmax, ns, population_strategy, strawberry_diversity_tolerance, strawberry_fitness_method)
3.4 constrained problem?
Determine whether the objective function also has information on feasibility.
constrained = 1; try [z g] = f(x0); catch err printf('Error identifier is %s\n', err.identifier); printf('Error message is %s\n', err.message); printf('\nThis could be due to the change in Strawberry that\n') printf('now requires the objective function to return a\n') printf('feasibility indication as well as the objective function\n') printf('value(s).\n\n') if (strcmp (err.identifier, 'Octave:undefined-function') || strcmp(err.identifier,'MATLAB:UndefinedFunction')) printf(': objective function is unconstrained.\n') constrained = 0; else ## not an error we expected to pass this on rethrow(err); endif end_try_catch if constrained printf(': objective function is constrained.\n'); endif
3.5 initial population
[phi, nx, nz, nf, ninf] = strawberry_newpopulation (x0,a,b,npop,f,constrained); pop = strawberry_sort (phi,nx,nz); gen = 0; best = []; #will be defined after fitness evaluation bestgen = gen; nfunctionevaluations = npop; # initial population size if output > 0 printf('In the following table, $n_f$ is number of feasible points,\n') printf('$n_i$ for infeasible, $n_p$ number in Pareto set\n'); printf('$c$ best constraint value and $g_b$ best generation.\n'); printf('| %9s |', 'gen') if nz > 1 for i=1:nz, printf(' $z_{%02d}$ |', i); endfor if constrained; printf(' %9s |', 'c'); endif else index = nx; if nx > 4 index = 4; endif for i=1:index; printf(' %6sx%02d |', '', i); endfor for i=1:nz; printf(' %6sy%02d |', '', i); endfor if constrained; printf(' %9s |', 'c'); endif endif printf(' %5s | %5s |', '$n_f$', '$n_i$') if nz > 1 printf(' %5s |', '$n_p$') else printf(' %5s |', '$g_b$') endif printf('\n'); printf('|-\n'); endif
3.6 iterate
while gen < ngen && (nz > 1 || gen < bestgen+ns) gen = gen + 1;
3.6.1 prune similar solutions to encourage diversity
Remove duplicate members as they contribute nothing.
## printf('npruned=%d nx=%d nz=%d\n', npruned, nx, nz) pop = strawberry_prune (pop, nx, nz); ## printf('npruned=%d nx=%d nz=%d\n', npruned, nx, nz)
3.6.2 rank solutions
The fitness method is used to find the best members of the population and assign each one a ranking N ∈ (0,1) with higher values better than lower values.
In the multi-objective case, the pareto front is combined with the elite set, a new pareto front is identified and duplicates are removed. The elite set does not get involved in the selection and propagation.
## evaluate the fitness of the population. For multi-objective problems, ## this has the side effect of returning the pareto front [N pareto] = strawberry_fitness (pop,nx,nz,size(pop,2)); ## populationstatistics('pareto',pareto,nx,nz); ## keep track of best. For multi-objective problems, this means keeping the pareto set debugprint(1, 'best', best) debugprint(1, 'pareto', pareto) debugprint(1, 'pop(1)', pop(:,1)) debugprint(1, 'nx, nz', [nx, nz]) if nz < 2 ... && (isempty(best) ... || length(best) < 1 ... || (pareto(nx+1) < best(nx+1) ... && norm(abs(best(1:nx)-pareto(1:nx))) > 1e-6)) best = pareto; bestgen = gen; ## zzz = zfit (best (1:nx)) if ~output printf('\n... new best solution at generation %d, z(1)=%g x=', gen, best(nx+1)); printf('%g ', best(1:nx)); printf('\n'); endif elseif nz>1 ## update the best to be the set of non-dominated points from the union ## of the old best and the current population but only include old ## best if we wish to archive solutions if strawberry_archive > 0 if isempty(best) || length(best) <= 1 best = pareto; else union = [best, pareto]; if length(union) < nx+nz+1 best = []; else best = strawberry_prune(union(:,findpareto(union(nx+1:nx+nz,:))),nx,nz); endif endif else best = pareto; endif debugprint (1, 'size of pareto: ', length(best)) endif
3.6.3 periodic output
There are two types of periodic output.
3.6.3.1 population statistics to console
The first, controlled by the output argument to the function, is a single line summary of the status of the current population. This defaults to outputting a total of 50 lines over the full evolution.
## populationstatistics('whole',pop,nx,nz); ## populationstatistics('best',best,nx,nz); if output > 0 && (0 == mod(gen,output) || 1 == gen) if strawberry_octave if strawberry_numberofprocessors > 1 dtime = time-starttime; else dtime = cputime-starttime; endif else dtime = toc; endif fprintf(stderr, '\r'); printf('| %9d |', gen); nfeas = sum(pop(end,:)<=0.0); ninfeas = sum(pop(end,:)>0); if nz > 1 if ~ isempty(best) && length(best)>1 ## printf('Size of best: %d %d\n',size(best)) printf (' %9.3g |', min(best(nx+1:nx+nz,:),[],2)) if constrained; printf(' %9.3g |', min(best(nx+nz+1,:))); endif else printf(' %9.3g |', zeros(nz+constrained,1)); endif printf(' %5d | %5d | %5d |', nfeas, ninfeas, size(best,2)); else if nx > 5 indices = [1:4 nx+nz]; else indices = 1:nx+nz; endif printf (' %9.3g |', best(indices)) if constrained; printf(' %9.3g |', best(nx+nz+1)); endif printf(' %5d | %5d | %5d |', nfeas, ninfeas, bestgen); endif printf(' \n'); else if nz > 1 ## [fitness pareto] = moga_fitness (pop(1:nx,:), pop(nx+1:nx+nz,:)); ## fprintf(stderr, '\r%30s %7d %3d/%4d %9.3g %9.3g %9.3g %9.3g', '', gen, size(best,2), length(pop), best(nx+1:nx+nz,1), best(nx+1:nx+nz,end)) fprintf(stderr, '\r%30s %7d %3d/%4d ', '', gen, size(best,2), length(pop)) else if constrained fprintf(stderr, '\r%30s %9d [%9d] %5d %13.6e %13.6e ', '', gen, bestgen, length(pop), best(nx+nz), best(nx+nz+1)); else fprintf(stderr, '\r%30s %9d [%9d] %5d %8d %13.6e ', '', '', gen, bestgen, length(pop), nfunctionevaluations, best(nx+nz)); endif endif endif debugprint (1,'strawberry: fitness', N); actualnpop = size(pop,2); if actualnpop < size (pop,2) printf('Ummmm size of population %d is less than expected (%d)\n', size(1,pop), npop); endif
3.6.3.2 pareto set to file
The second is the output of the full population to an automatically named file (based on time stamp and generation number). The default is to not generate this output. This output is controlled by setting the global variable strawberry_output_population which should be set to a positive number that specifies which generations to output (modulo == 0).
This output is only available for multi-objective problems and a file will be saved only if there is at least one feasible member in the population.
if strawberry_octave if strawberry_output_population > 0 ... && 0 == mod(gen,strawberry_output_population) filename = sprintf('%s-%s-%06d.txt', 'strawberry-population', ... strftime('%Y%m%d-%H%M%S', localtime(time())), ... gen); [sorted sortindices] = sort(best(nx+1,:)); poptrans = best(:,sortindices)'; save('-text',filename,'poptrans'); endif endif
3.6.4 select and propagate
## generate all the new points and then evaluate them in parallel n = 1; newpop = []; selected = []; for p=1:npop # we pick up to NPOP members to propagate s = strawberry_select (N); debugprint(2,'selected index', s) if s > 0 selected(:,p) = pop(:,s); # selected members remain for next generation; others die off debugprint(3, 'selected fitness and point: ', [N(s), pop(:,s)']); nr = strawberry_runners (N(s),nrmax); # number of runners debugprint(2,': number of runners', nr) for r=1:nr newpop{n} = strawberry_neighbourfn(pop(1:nx,s), a, b, N(s)); debugprint(2, ': added new member to population: ', newpop{n}) n = n + 1; ## endif endfor ## set fitness so this member is not selected again N(s) = -1; endif endfor debugprint(1,'Size of selected set: ', size(selected)) debugprint(1,'Size of newpop: ', size(newpop)) ## evaluate these in parallel using an appropriate number of processors ##parf = @(x) if length(x)>nx, x', else [x, f(x), 0]', endif ##phi = parcellfun (strawberry_numberofprocessors, parf, newpop)'; if strawberry_numberofprocessors > 1 if constrained phi = parcellfun (strawberry_numberofprocessors, @(x) [x; f(x); g(x)], newpop, 'VerboseLevel', 0); else phi = parcellfun (strawberry_numberofprocessors, @(x) [x; f(x); 0], newpop, 'VerboseLevel', 0); endif else #sequential evaluation n = length(newpop); x = newpop{1}; if constrained [y g] = f(x); else y = f(x); g = 0; endif phi = zeros(length(x)+length(y)+1,n); phi(:,1) = [x;y;g]; for i=2:n x = newpop{i}; nf = nf + 1; if constrained [y g] = f(x); if g > 0 ninf = ninf + 1; endif else y = f(x); g = 0; endif phi(:,i) = [x;y;g]; endfor endif nfunctionevaluations = nfunctionevaluations + length(phi); debugprint (1, ': phi before removal of infeasible solutions', phi) ntotal = size(phi,2);
3.6.5 create new population
## sort the population, which is composed of the original NPOP ## best plus those created in this loop, using the fitness for ## sorting. ## we have three sets of solutions that we can combine to create a ## new population: ## 1. the best overall so far ## 2. the members selected from the previous generation for propagation ## 3. and the new propagated solutions ## there are therefore 3! combinations although we always should ## include the new solutions so really have 4 different options: ## new alone, new with best, new with selected and new with ## selected and best. ## fprintf(stderr, 'size best=%d selected=%d phi=%d\n', size(best,2), size(selected,2), size(phi,2)); ## cater for when best array is empty ps = population_strategy; if ps > 2 && length(best) > (npop/2) ## do not do elitism if pareto set too large; kludge! ps = ps - 2; endif switch (ps) case 1 # new members alone pop = phi; case 2 # new with selected pop = [selected, phi]; case 3 # new with best pop = [best, phi]; case 4 # new with best and selected pop = [best, selected, phi]; otherwise printf('Error: population strategy %d not recognised.', population_strategy) endswitch
3.7 end loop and finish function
endwhile if gen < ngen printf('\n: strawberry terminating condition satisfied due to lack of improvement at gen=%d\n', gen); endif if output printf('\n: strawberry at end, nf=%d ninf=%d best solution:\n', nf, ninf) disp(best'); endif ## ensure the best solution is returned pop = [best, pop]; x = pop(1:nx,:); z = pop(nx+1:end,:); if strawberry_octave if strawberry_numberofprocessors > 1 endtime = time; # wall clock time else endtime = cputime; endif else endtime = toc; endif printf('\n: strawberry method elapsed time: %.1f with %d functions evaluated and %d solutions pruned with %d similar.\n', ... endtime-starttime, nf, npruned, nsimilar) printf('MOSD improvements: %d\n', mosd_numberimproved); endfunction
4 Support functions
4.1 distance – default implementation
The distance method determines how far to send a runner. The first argument is the fitness, ![\(f \in [0,1]\)](ltxpng/strawberry_14e0080491cf17c0a6ac4b5f58bbb8588468a92e.png) , and the second is the dimension of the problem,
, and the second is the dimension of the problem,  , i.e. the number of decision variables.
, i.e. the number of decision variables.
The basic premise is that the fitter the solution, the less far runners are sent as there is plenty of food in this local neighbourhood. A less fit point will send runners further.
function d = strawberry_distance(f,n) d = (1-f) * 2*(rand(n,1)-0.5); endfunction
4.2 fitness – for single and multi-objective functions
The fitness of the members in the population is calculated differently for 1 criterion problems and multi-criteria problems. The former is based on a scaled value within the range of values for feasible and infeasible solutions separately.
For multi-objective problems, we have a number of options. We can use the approach we used in MOGA which was based on distance to the Pareto set of non-dominated solutions. However, this has a problem when the set is large compared with the total population size. Also, it does not necessarily push towards the endpoints of the Pareto front which is often, in the problems we consider, what we want.
To accomplish the latter, we consider a ranking that takes into account how good each individual objective value is within its own set of values. If we consider a fitness 1,… for each point for each objective, and then multiply these two ranking values together, this should emphasise the end-points. The multiplication of vectors of rankings in known as the Hadamard product.
function [fit, best] = strawberry_fitness(p,nx,nz,npop) global strawberry_fitness_method [n m] = size(p); debugprint (1, 'fitness, nx nz m n npop', [nx, nz, m, n, npop]) if m <= 0 disp('No solutions in the population'); endif fit = zeros(m,1); factor = 1; # for placement in fitness interval (0,1) indexfeasible = p(n,:) <= 0; nfeas = sum(indexfeasible); indexinfeasible = p(n,:) > 0; ninfeas = sum(indexinfeasible); if nfeas > 0 feasiblefit = strawberry_vectorfitness(nz, p(nx+1:nx+nz,indexfeasible)); ## the ranking of the feasible solutions is possibly adjusted to ## fit in only the upper half of the [0,1] interval if there are ## infeasible solutions as well. The latter will have fitness ## values in the bottom half of the interval. if ninfeas > 0 factor = 2; end fit(indexfeasible) = (feasiblefit+factor-1)/factor; end if ninfeas > 0 ## squeeze infeasible fitness values into (0,0.5) or (0,1) ## depending on factor, i.e. whether there are any feasible ## solutions as well or not fit(indexinfeasible) = strawberry_vectorfitness(1, p(n,indexinfeasible))/factor; end if nz < 2 [bestfit index] = max(fit); best = p(:,index); else ## printf('There are %d feasible solutions when calculating fitness\n',nfeas) if nfeas > 0 allindices = 1:m; feasibleindices = allindices(indexfeasible); ## printf('feasible population:\n') ## disp(p(:,indexfeasible)) ## printf('and pareto from that population\n') ## disp(p(:,feasibleindices(findpareto(p(nx+1:nx+nz,indexfeasible))))) best = p(:,feasibleindices(findpareto(p(nx+1:nx+nz,indexfeasible)))); else best = []; endif endif endfunction
function fit = strawberry_vectorfitness(m,v) ## println("VF: v=$v") ## println(" : of size $(size(v))") if m == 1 # single objective l = length(v); [sorted indices] = sort(v); zmin = v(indices(1)); zmax = v(indices(l)); if l == 1 || abs(zmax-zmin) < eps() fit = 0.5*ones(1,l); else ## avoid extreme 0,1 values fit = tanh((zmax - v) / (zmax - zmin) - 0.5)+0.5; end else # multi-objective [m, l] = size(v); rank = ones(m,l); #rank of each solution for each objective function for i=1:m [sorted indices] = sort(v(i,:)); rank(i,indices) = 1:l; end ## hadamard product of ranks fitness = prod(rank); ## normalise and reverse meaning (1=best, 0=worst) if l == 1 fit = 0.5; else ## avoid extreme 0,1 values fit = tanh(0.5 - fitness / max(fitness)) + 0.5; end end ## println("VF: fit=$fit") end
4.3 initialise – default values and version information
function strawberry_initialise global strawberry_version global strawberry_numberofprocessors global strawberry_octave global moga_version global mosd_version if isempty (strawberry_version) strawberry_version = '2019.06.24 12:21:04'; mosd_initialise moga_initialise printf (': STRAWBERRY %s, main function\n', strawberry_version) printf (': using MOSD %s, multi-objective steepest descent method.\n', mosd_version) printf (': and MOGA %s, multi-objective genetic algorithm fitness function.\n', moga_version) strawberry_octave = exist ('OCTAVE_VERSION', 'builtin') > 0; if strawberry_octave printf(': running in Octave\n') if strawberry_numberofprocessors > 1 pkg load parallel #need parcellfun in particular endif endif endif
We define default functions for the key steps in the strawberry algorithm:
- new random solution
- generate a random solution in the search space
- neighbour
- given an existing point in the search space, generate a new solution based on the fitness value (0<f<1 with 1 most fit) given
These functions allow strawberry to be used for more general problems than just nonlinear programming problems. The default functions, however, are suitable for compact domains defined by bounds in the R^n.
global strawberry_neighbourfn global strawberry_randomsolutionfn if isempty(strawberry_randomsolutionfn) strawberry_randomsolutionfn = @strawberry_randomsolution; printf (': using default random solution generator function.\n'); endif if isempty(strawberry_neighbourfn) strawberry_neighbourfn = @strawberry_neighbour; printf (': using default neighbouring solution generator function.\n') endif
4.4 isdiverse – identify solutions that differ
We only want to add solutions to the population that are diverse, i.e. significantly different, from those that are already there. However, the diversity control should not be at the expense of losing better solutions. The current implementation is not good in this respect and should be used with care as a result.
function diverse = strawberry_isdiverse (pop, x) global nsimilar global strawberry_diversity_tolerance i = 0; diverse = 1; while i < length(pop) && diverse diverse = norm(pop{i}-x) > strawberry_diversity_tolerance; i = i + 1; endwhile if ~ diverse, nsimilar = nsimilar + 1; endif endfunction
4.5 neighbour – for compact real valued domains
Given a fitness value, f ∈ (0,1), a point in the search space, x, and the lower, a and upper, b, bounds, generate a new point in the space. The better the fitness, i.e. closer to 1, the closer the point should be to the given point. The basis of the Strawberry algorithm is that fitter points generate more points in the local area; less fit points generate fewer new points but further away. Exploitation versus exploration.
The default implementation uses the fitness to define a distance within the bounds of the variables for each dimension.
function n = strawberry_neighbour(x,a,b,f) nx = length(x); dx = (b-a)/2 .* strawberry_distance (f,nx); # how far to run ## fprintf(stderr, 'Selected %d with fitness %g to move %g\n', s, N(s), norm(dx)) debugprint(3, ': dx', dx(1:nx)) n = x+dx; n(n<a) = a(n<a); # reset to boundary n(n>b) = b(n>b); # reset to boundary endfunction
4.6 newpopulation – create an initial population
Create a random population, distributed uniformly (hopefully) throughout the domain defined by the lower and upper bounds of the optimisation variables.
function [pop, nx, nz, nf, ninf] = strawberry_newpopulation (x0,a,b,npop,f,constrained) global strawberry_randomsolutionfn global strawberry_numberofprocessors nx = length(x0); printf(': %d decision variables\n', nx); nf = 0; ninf = 0; pop = []; # will be array of x+y values n = 0; ntries = 0; xcell{1} = x0; # start with initial guess for i=2:npop xcell{i} = strawberry_randomsolutionfn(a,b); endfor if strawberry_numberofprocessors > 1 if constrained pop = parcellfun (strawberry_numberofprocessors, ... @(x) [x; f(x); g(x)], xcell, 'VerboseLevel', 0 ... ); else pop = parcellfun (strawberry_numberofprocessors, ... @(x) [x; f(x); 0], xcell, 'VerboseLevel', 0); endif else #sequential operation x = xcell{1}; if constrained [z g] = f(x); else z = f(x); g = 0; endif y = [x; z; g]; pop = zeros(length(y),npop); pop(:,1) = y; for i=2:npop x = xcell{i}; nf = nf+1; if constrained [z g] = f(x); else z = f(x); g = 0; endif pop(:,i) = [x; z; g]; endfor ## pop = cellfun (@(x) [x; f(x); 0], xcell); endif mtotal = size(pop,2); [n m] = size(pop); ninf = ninf + mtotal - m; ## each row consists of nx x values, nz y values and a feasibility ## indication nz = n-nx-1; printf(': %d objective function values\n', nz); endfunction
4.7 populationstatistics – mostly for debugging
function populationstatistics(s,p,nx,nz) [m n] = size(p); feasible = p(end,:) <= 0; nfeasible = sum(feasible); infeasible = p(end,:) >= 0; ninfeasible = sum(infeasible); printf('Population statistics for %s:\n', s) printf(': there are %d members of which %d are feasible.\n', n, nfeasible) printf(': min objective function values: ') printf('%g ', min(p(nx+1:nx+nz,:),[],2)) printf('\n'); if nfeasible > 0 printf(': constraint values for feasible solutions in [%g,%g]\n', ... min(p(end,feasible)), max(p(end,feasible))); endif if ninfeasible > 0 printf(': constraint values for infeasible solutions in [%g,%g]\n', ... min(p(end,infeasible)), max(p(end,infeasible))); endif endfunction
4.8 prune – remove non-diverse members
Especially for multi-objective problems, we have a problem with diversity in that the pareto set forms an elite set. If this set has multiple copies of the same solutions, the set can grow quite large and increases the computational effort dramatically with little effect on the quality of the solutions obtained.
function pruned = strawberry_prune (pop, nx, nz) global npruned global strawberry_diversity_tolerance npop = size(pop,2); if npop > 0 pruned = pop(:,1); np = 1; # size of pruned set for i=2:npop diverse = 1; j = 0; while diverse && j < np j = j + 1; ## diversity based on x values alone diverse = norm (pop(1:nx,i)-pruned(1:nx,j)) > strawberry_diversity_tolerance; ## printf('div(%d,%d)=%g %d\r', i, j, norm (pop(1:nx,i)-pruned(1:nx,j)), diverse); endwhile if diverse pruned = [pruned, pop(:,i)]; np = np + 1; #keep track of how many copied over else ## prune one or the other. ideally, we keep the better ## one. If we cannot distinguish (in a multi-objective ## sense), we simply keep the one that is already there. npruned = npruned + 1; if ~ dominates(pruned(nx+1:nx+nz,j),pop(nx+1:nx+nz,i)) if dominates(pop(nx+1:nx+nz,i),pruned(nx+1:nx+nz,j)) ## current solution is better, i.e. dominates, than previous ## one so replace pruned(:,j) = pop(:,i); endif endif endif endfor endif endfunction
4.9 random solution – generate a new solution
Given the lower, a and upper, b, bounds, generate a random point in the search space. By default, this function returns a random solution in a compact hypercube domain in R^n defined by the bounds on the variables, ![\(x \in \bbcode{R}^n \cap [a,b]\)](ltxpng/strawberry_ccf3e970f9f11b0d14560e55cae25fcfb27d6df7.png) .
.
function x = strawberry_randomsolution(a, b) r = rand(length(a),1); x = a + r.*(b-a); endfunction
4.10 runners – number a function of fitness
Two aspects define a plant propagation algorithm: the distance for the runners to propagate and the number of such runners that are generated. This function addresses the latter. The better the solution, defined by the fitness  , the more runners should be generated. The actual number of runners is
, the more runners should be generated. The actual number of runners is ![\(\in [1,N_{r,max}]\)](ltxpng/strawberry_4c56c13acb4f535f37e9003e7d74a42defbc1e64.png) and is randomly generated.
and is randomly generated.
function nr = strawberry_runners(N, nrmax) r = rand(); nr = ceil (nrmax*N*r); # number of runners if nr < 1, nr = 1; endif debugprint (4, ':runners N r runners max', [N, r, nr, nrmax]) endfunction
4.11 select – tournament fitness based selection
Selection from the current population, for propagation of runners, is based on a sample size 2 tournament selection. This could be generalised to have a greater number of individuals selected for a tournament, emphasising the most fit solutions. Other selection approaches could of course be used instead. Our experience is that this simple selection procedure is effective in balancing the global and local search aspects of a plant propagation algorithm.
The one modification we have with respect to the standard selection procedure is that we only select from those individuals that have not already been selected in the current generation.
function s = strawberry_select (N) ## select only from those solutions that have not been selected ## before, i.e. those with non-negative fitness values n = length(N); available = N >= 0; debugprint (4, 'select, available = ', available) na = sum(available); allpossibleindices = 1:n; indices = allpossibleindices(available); switch na case 0 s = 0; #no solutions available. case 1 s = indices(1); #only one available so select it case 2 if N(indices(1)) > N(indices(2)) s = indices(1); else s = indices(2); endif otherwise i = ceil(na * rand(2,1)); i(i>na) = na; i(i<1) = 1; if N(indices(i(1))) > N(indices(i(2))) s = indices(i(1)); else s = indices(i(2)); endif endswitch if s>0 debugprint(5, 'select: s N(s)', [s, N(s)]) else debugprint(5, 'select: none available for selection') endif endfunction
4.12 sort – for single criterion problems
For single criterion problems, we sort the population in order of decreasing fitness. This is purely for the purpose of output and could be removed entirely.
function pop = strawberry_sort (pop,nx,nz) [n m] = size(pop); ## sorting only makes sense in single criterion problems if nz == 1 # single objective optimisation if n-nx == 2 # y + constraint violation # find feasible and infeasible sets feasible = pop(:, pop(n,:) <= 0); [s, i] = sort(feasible(nx+1,:)); # sort on objective function value feasible = feasible(:,i); # sorted ## now check for infeasible solutions nfeasible = size(feasible,2); if nfeasible < size(pop,2) infeasible = pop(:, pop(n,:) > 0); [s, i] = sort(infeasible(n,:)); infeasible = infeasible(:,i); pop = [feasible, infeasible]; else pop = feasible; endif else error('Number of objective functions does not seem to match'); endif endif endfunction
5 Tests
5.1 general bicriteria test
strawberry_test
function [z g] = strawberry_testobjective(x) z = [ sum((x-0.5).^2+1) sum(cos(x))]; g = 0; endfunction
function [x z pareto fitness] = strawberry_test global esfdebug esfdebug = 0 global strawberry_numberofprocessors strawberry_numberofprocessors = 1; x0 = [0 0 0 0 0]'; a = zeros(5,1); b = ones(5,1); printf('Testing bicriteria problem with %d decision variables\n', length(x0)) printf('starting with initial point '), x0 z0 = strawberry_testobjective(x0) printf('which has objective %d function values ', length(z0)) for i=1:length(z0) printf('%f ', z0(i)) endfor printf('\n') ## [x y nf ninf bestgen] = strawberry(x0, a, b, f, ngen, npop, nrmax, ns, population_strategy, output, g) [x z nf ninf bestgen] = strawberry(x0, a, b, @strawberry_testobjective, 200, 50); paretoset = z(1:2, findpareto(z(1:2,:))); [zz indices] = sort(paretoset(1,:)); paretoset = paretoset(:,indices) plot(paretoset(1,:),paretoset(2,:),'- r',z(1,:),z(2,:),' *g')
5.2 three criteria test
This is simple test of three criteria. The results can be seen in the following plot which shows the solutions in the Pareto set at the end.
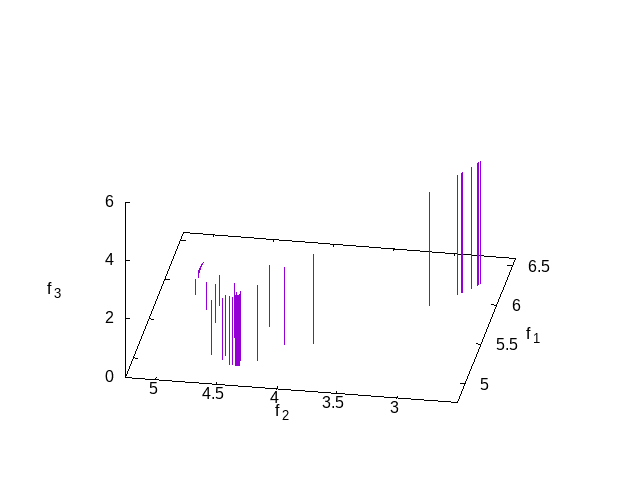
function [z g] = strawberry_test3objective(x) z = [ sum((x-0.5).^2+1) sum(cos(x)) sum(sin(x))]; g = 0; endfunction
function [x z paretoset] = strawberry_test3 global esfdebug esfdebug = 0 global strawberry_numberofprocessors strawberry_numberofprocessors = 1; global strawberry_fitness_method strawberry_fitness_method = 0 global strawberry_output_population strawberry_output_population = 100 x0 = [0 0 0 0 0]'; a = zeros(5,1); b = ones(5,1); printf('Testing three criteria problem with %d decision variables\n', length(x0)) printf('starting with initial point '), x0 z0 = strawberry_test3objective(x0); printf('which has objective %d function values ', length(z0)) for i=1:length(z0) printf('%f ', z0(i)) endfor printf('\n') ## [x y nf ninf bestgen] = strawberry(x0, a, b, f, ngen, npop, nrmax, ns, population_strategy, output, g) [x z nf ninf bestgen] = strawberry(x0, a, b, @strawberry_test3objective, 1000, 20) paretoset = z(1:3, findpareto(z(1:3,:))); [zz indices] = sort(paretoset(1,:)); paretoset = paretoset(:,indices) plot3(paretoset(1,:),paretoset(2,:), paretoset(3,:),'- r',z(1,:),z(2,:), z(3,:),' *g')
5.3 testing the use of alternative random solutions and neighbour generation for mixed integer problems
The assumption is that Strawberry itself needs no special knowledge to work with integer variables. The problem encoded here is from Westerlund:

subject to

with real valued ![\(x \in [1,6]\)](ltxpng/strawberry_7a26ac0041796e1562d6612279a15e12d3f3592e.png) and integer valued
and integer valued ![\(y \in[1,6]\)](ltxpng/strawberry_654ca491046266519cb8adb4980b4dcfa152fc80.png) .
.
This test case exercises three elements:
- the random generation of solutions in the search space
- the generation of neighbouring solutions
- the use of constraints
5.3.1 helper functions for solution generation
We need to define two functions:
- generate a random solution in the search space
function x = mitestrandom(a,b) x = [ a(1)+(b(1)-a(1))*rand() a(2)+round((b(2)-a(2))*rand()-0.5)]; x(x>b) = b(x>b); endfunction
- generate a neighbouring solution based on the fitness
function x = mitestneighbour(x0, a, b, f) x = x0 + (1-f)*(rand(length(x0),1)-0.5).*(b-a); x(2) = round(x(2)); x(x<a) = a(x<a); x(x>b) = b(x>b); endfunction
Note the use of hard-code values for the lower (1) and upper (6) bounds on both variables. These are used for the bounds checking in the second function and for generating suitable random points within the bounded domain in the first function.
5.3.2 the actual problem and solution method
The objective function and constraints are defined in a single Octave function. The value of the objective function is simple; there are three constraints, all meant to be less than or equal to 0. g will be true if any of the constraints are violated.
function [f g] = mitestf(x) f = 3*x(2)-5*x(1); g = max([ 2*x(2) + 3*x(1) - 24; 3*x(1) - 2*x(2) - 8; 2*x(2)^2 - 2*sqrt(x(2)) + 11*x(2) + 8*x(1) - 39 - 2*sqrt(x(1))*x(2)^2 ]); endfunction
Strawberry is used on this objective function within a simple rectangle domain.
global esfdebug esfdebug = 0 global strawberry_numberofprocessors strawberry_numberofprocessors = 1; global strawberry_randomsolutionfn strawberry_randomsolutionfn = @mitestrandom; global strawberry_neighbourfn strawberry_neighbourfn = @mitestneighbour; a = [1;1]; b = [6;6]; x0 = [4;1]; ngen = 100; npop = 10; nrmax = 5; ns = 1000; #number of stable generations population_strategy = 4; output = 10; [x y nf ninf bestgen] = strawberry(x0, a, b, @mitestf, ngen, npop, nrmax, ns, population_strategy, output)
6 Recent change history
2018-10-19 cleaned up HTML and use new style with fixed TOC 2018-05-30 added major revision entry 2018-05-30 improved commentary for neighbour and random point functions 2018-05-30 refactor: lower and upper bounds passed through to underlying functions 2018-05-21 fixed typo in headline 2018-05-10 added more details for the MINLP test example 2018-01-02 task counting is recursive 2018-01-02 incorporated actions from EGL 2017 conference 2017-11-24 changed file name for saving the pareto front 2017-11-23 fixed tic/toc usage