Calling python code from Julia for objective function in optimization
A significant part of my research is embodied in the Fresa nature inspired multi-objective optimization package (Fraga 2021) implemented in the Julia language.1 Up until now, all the projects in my group that have made use of Fresa have involved writing all process models in Julia. Good.
However, there are times when it makes sense to use code written in other languages. One such case has recently arisen (details to follow eventually) where the models to be used have been written in Python. These are complex models so translating them to Julia would not be an efficient use of our time. But it turns out there is no need to do such a translation. Julia has a package for this purpose: PyCall.jl.2
Using PyCall is straightforward. Consider the simple optimization problem (from the Fresa introduction in the main documentation):
![\[ \min_x z = 5 x_1^2 + 4 x_2^2 - 60 x_1 - 80 x_2 \]](ltximg/20250623_d7e8c488dfb4b8a1bd72dad867a4a6560bd26cc4.png)
subject to the following constraints
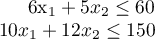
and with ![\(x_1 \in [0,8]\)](ltximg/20250623_6bbd7a63b1d644d0829ba6dba488079c18042f51.png) and
and ![\(x_2 \in [0,\infty]\)](ltximg/20250623_0140fc08aebb3f20897bf3f31657bbd2ab74d35d.png) .
.
The python implementation of this objective function, meeting the requirements of Fresa which are to return the objective function value and the violation of constraints, follows:
def objective(x): # (single) objective function value z = 5*x[0]**2 + 4*x[1]**2 - 60*x[0] - 80*x[1] # contraints (rewritten in form g(x) ≤ 0) g = [6*x[0] + 5*x[1] - 60, 10*x[0] + 12*x[1] - 150] # return objective function value along with largest constraint return (z, max(g))
This code blog is included in the source for this blog post as an org Babel src block, such as
#+begin_src python :tangle code/model.py :exports code :noweb yes # python code here #+end_src
which not only tells the org mode exporter (for creating the HTML code) that only the code should be exported, it also indicates where to put the code when tangled, specifically in a sub-directory code with the file name model.py. The specifications also indicate that the code block can be referenced by other code blocks (noweb).
The function defined in the code block can be evaluated:
print(objective([1,3]))
which yields
(-259, -39)
where the first value in the tuple is the objective function and the second is the largest value of the left hand sides of the constraints.3
The above python code has been tangled to the file, specifically ./code/model.py, which allows us to refer to the function as a module in Python, a module named model. Having done this, we can now use PyCall from Julia to access that function:
# the PyCall package allows us to access python code using PyCall let # tell python where our module can be found: the code # sub-directory pushfirst!(pyimport("sys")."path", "code") # bring in the module model = pyimport("model") # and now evaluate the objective function at a given point println(model.objective([1,3])) end
where, in the first line of the let block, I have told python where to find the module defined above: the code sub-directory where I have told org to tangle the code to. I use the let block to hide uninteresting output. The actual output from running this Julia code is
# -*- mode: org; -*- #+startup: show3levels (-259, -39)
Note that the first two lines of the output come from my ~/.julia/config/startup.jl file. Most of the code I write in Julia assumes that the output will be read from within Emacs and org mode is my preferred mode for reading and writing text. The first line tells Emacs to use org mode when visiting the file with the output. The second line tells org mode itself to start up with content hidden and with up to three levels of headings visible.
Unsurprisingly, the actual output from the code above is the same as running the python code directly.
Now that we can access the python code, we can use Fresa to solve the optimization problem defined by that objective function and the constraints given above:
# use Fresa to solve the optimization problem using Fresa # PyCall provides the interface between Julia and python using PyCall let # include the sub-directory "code" for searching for modules pushfirst!(pyimport("sys")."path", "code") # bring in the python module defined above model = pyimport("model") # define the starting population which consists of a single point in # the domain. x0 = [0.0, 8.0] p0 = [Fresa.Point(x0, model.objective)] # define the lower and upper bounds for the search domain a = [0.0, 0.0] # lower bounds b = [8.0, 12.5] # upper bounds # and finally invoke the solve method in the Fresa package to find the # optimum best, population = Fresa.solve(model.objective, p0, lower = a, upper = b) println("Best solution found at $(best.x)") if best.g ≤ 0 println("which is feasible and has objective function value $(best.z)") else println("which is infeasible with constraint violation $(best.g)") end end
The output of running this Julia code, using the python objective function implementation is:
# -*- mode: org; -*- #+startup: show3levels # Fresa 🍓 PPA v8.2.1, last change [2024-07-15 13:16+0100] * Fresa solve PyObject <function objective at 0x7f2cbd1a7ce0> [2025-06-20 15:31] #+name: PyObject <function objective at 0x7f2cbd1a7ce0>settings | variable | value | |- | elite | true | | archive | false | | ϵ | 0.0001 | | fitness | scaled | | issimilar | nothing | | multithreading | false | | nfmax | 2147483647 | | ngen | 100 | | np | 10 | | nrmax | 5 | | ns | 100 | | steepness | 1.0 | | tournamentsize | 2 | |- : function evaluations performed sequentially. ** initial population #+name: PyObject <function objective at 0x7f2cbd1a7ce0>initial |- | z1 | g | x | |- | -384.0 | -20.0 | [0.0, 8.0] | |- ** evolution #+name: PyObject <function objective at 0x7f2cbd1a7ce0>evolution #+plot: ind:1 deps:(6) with:"points pt 7" set:"logscale x" | gen | pop | nf | pruned | t (s) | z1 | g | |- | 1 | 1 | 1 | 0 | 3.36 | -384.0 | -20.0 | | 2 | 2 | 2 | 0 | 4.78 | -384.0 | -20.0 | | 3 | 4 | 5 | 0 | 4.78 | -387.82785945592724 | -19.200940486071467 | | 4 | 13 | 17 | 0 | 4.78 | -396.1719956122356 | -18.475690406938213 | | 5 | 17 | 33 | 0 | 4.88 | -465.2747783651207 | -6.30274504212872 | | 6 | 31 | 63 | 0 | 4.88 | -465.8524502124965 | -6.408778832873729 | | 7 | 17 | 79 | 0 | 4.88 | -501.79991137112324 | -5.031258553399482 | | 8 | 26 | 104 | 0 | 4.88 | -501.79991137112324 | -5.031258553399482 | | 9 | 30 | 133 | 0 | 4.88 | -502.8589673535681 | -4.720801363767805 | | 10 | 22 | 154 | 0 | 4.88 | -502.8589673535681 | -4.720801363767805 | | 20 | 38 | 451 | 0 | 4.88 | -529.4160416826105 | -0.07591111774389958 | | 30 | 35 | 756 | 0 | 4.89 | -529.7007028783921 | -0.003834279528547313 | | 40 | 29 | 1053 | 0 | 4.89 | -529.7007028783921 | -0.003834279528547313 | | 50 | 22 | 1337 | 0 | 4.89 | -529.7007028783921 | -0.003834279528547313 | | 60 | 33 | 1652 | 0 | 4.89 | -529.7265560193542 | -0.0005705081069180551 | | 70 | 29 | 1910 | 0 | 4.90 | -529.7265560193542 | -0.0005705081069180551 | | 80 | 30 | 2191 | 0 | 4.90 | -529.7265560193542 | -0.0005705081069180551 | | 90 | 37 | 2477 | 0 | 4.90 | -529.7353127963394 | -0.0010852854197764827 | | 100 | 31 | 2799 | 0 | 4.90 | -529.7353127963394 | -0.0010852854197764827 | ** Fresa run finished : nf=2824 npruned=0 Best solution found at [3.685192837895438, 7.577551537441519] which is feasible and has objective function value [-529.7353127963394]
This output looks similar to that obtained using a Julia implementation of the objective function (see the introductory example in the documentation for Fresa).
Blog navigation
| Previous post | Blog | Next post |
|---|---|---|
| Using outline mode in Emacs for Julia code | Index | Navigating Julia source code files using Xref in Emacs |
You can find me on Mastodon or you can email me should you wish to comment on this entry or the whole blog.