3.03 Quotient topology: group actions
Video
Below the video you will find accompanying notes and some pre-class questions.
- Previous video: 3.02 Quotient topology: continuous maps.
- Index of all lectures.
Notes
(0.00) In this section, we will look at another kind of quotient space which is very different from the examples we've seen so far. Instead of making identifications of sides of polygons, or crushing subsets down to points, we will be identifying points which are related by symmetries.
Group actions
(0.33) An action of a group \(G\) on a set \(X\) is a homomorphism \(\rho\colon G\to Perm(X)\), where \(Perm(X)\) is the group of permutations of the set \(X\).
In other words, for each element \(g\in G\), I get a permutation \(\rho(g)\colon X\to X\) called the action of \(g\)). Because \(\rho\) is a homomorphism, if we act using \(g_1\) and then \(g_2\) we get the same permutation as if we had acted using \(g_2g_1\). Also, if we act using the identity, we get the identity permutation.
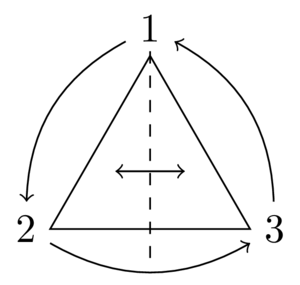
(1.36) The symmetry group of an equilateral triangle, \(D_3\), acts on the vertices \(\{1,2,3\}\) of the triangle, so we get a homomorphism \(\rho\colon D_3\to S_3=Perm(\{1,2,3\})\) (\(\rho\) happens to be an isomorphism in this example). For example, a reflection in the perpendicular bisector of the angle at vertex \(1\) acts as the transposition \((2,3)\); the anticlockwise rotation by \(120\) degrees acts as the cyclic permutation \((1,2,3)\).
Continuous group actions on topological spaces
(3.02) A continuous group action is a homomorphism \(\rho\colon G\to Perm(X)\) where \(X\) is a topological space and, for all \(g\in G\), \(\rho(g)\) is a homeomorphism of \(X\).
(4.06) In fact, it is sufficient to specify that \(\rho(g)\) is continuous, because its inverse will be \(\rho(g^{-1})\) which is then continuous by assumption.
(4.46) Take \(X=\mathbf{R}\) and \(G=\mathbf{Z}\). For each \(n\in \mathbf{Z}\), let \(\rho(n)\) be the translation \(x\mapsto x+n\). This is a continuous group action.

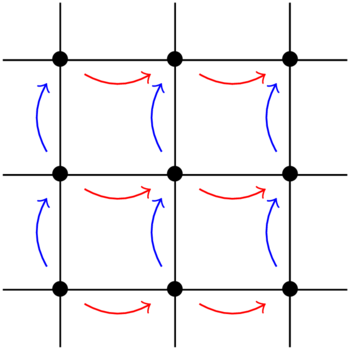
(6.01) Take \(X=\mathbf{R}^2\) and \(G=\mathbf{Z}^2\). For each pair of integers \((m,n)\in\mathbf{Z}^2\) we define \(\rho(m,n)\) to be the map \((x,y)\mapsto (x+m,y+n)\). In the figure, \((1,0)\in\mathbf{Z}^2\) acts by translating as indicated by the red arrows and \((0,1)\) acts via the blue arrows. The dots indicate (part of an infinite) equivalence class.
Quotients by group actions
(7.35) Given a group action \(\rho\colon G\to Perm(X)\) we get an equivalence relation on \(X\): \[x\sim y\mbox{ if and only if there exists }g\in G\mbox{ such that }gx=y.\] We write \(X/G\) for the quotient space \(X/\sim\).
(8.30) In the example of \(\mathbf{Z}\) acting on \(\mathbf{R}\) above, the equivalence class of \(x\) is the set of all real numbers whose fractional part is equal to the fractional part of \(x\). For example: all integers are equivalent; all integers-plus-a-half are equivalent, etc. The quotient \(\mathbf{R}/\mathbf{Z}\) is the circle: every point is equivalent to its fractional part in \([0,1)\) and \(0\sim 1\), so we get the same quotient as \([0,1]/\{0,1\}\), which is the circle.
(9.57) In the example \(\mathbf{R}^2/\mathbf{Z}^2\), any point can be translated by the action of \(\mathbf{Z}^2\) to the square \([0,1]\times[0,1]\) and the opposite sides are identified by translations in the \((1,0)\)- and \((0,1)\)-directions, so the quotient is precisely the 2-torus \(T^2\). This is not surprising: the 2-torus is homeomorphic to \(S^1\times S^1\) and this example is the product of two copies of the previous example.
(10.36) Let \(X=S^1=\{z\in\mathbf{C}\ :\ |z|=1\}\) and let \(G\) be the group of \(n\)th roots of unity for some \(n\). Then \(G\) acts on \(S^1\) by rotations: \(e^{i2\pi k/n}\) acts on \(e^{i\theta}\) by \(\rho(e^{i2\pi k/n})=e^{i\theta}\mapsto e^{i(\theta+2\pi k/n)}\).
(12.20) You can see that the quotient is \(S^1\) again: you move around from \(1\) to \(e^{i2\pi/n}\) at which point you return to the same equivalence class. Let's justify this more carefully.
(13.03) There is a continuous map \(F\colon S^1\to S^1\) defined by \(F(z)=z^n\) and it descends to the quotient \(S^1/G\) because \(F(e^{i2\pi kn}z)=F(z)\). By the lemma we proved about continuous functions on quotient spaces, we get a continuous function \(\bar{F}\colon S^1/G\to S^1\). The map \(F\) is \(n\)-to-\(1\), but the map \(\bar{F}\) is bijective.
(15.08) Using a theorem we proved about homeomorphisms, we see that \(\bar{F}\) is a homeomorphism provided \(S^1\) is Hausdorff (which is true because \(S^1\) is a subset of a Hausdorff space) and \(S^1/G\) is compact (because quotients of compact spaces are compact).
Quotient maps for group actions
(15.57) Let \(X\) be a space and let \(G\) be a group which acts continuously on \(X\). Then \(q\colon X\to X/G\) is open, i.e. the image of any open set is open.
(17.24) Let \(U\subset X\) be an open set. Its image \(q(U)\) is open if and only if \(q^{-1}(q(U))\) is open in \(X\) (by definition of the quotient topology).
(18.11) Unfortunately, \(q^{-1}(q(U))\) is not equal to \(U\) in general, so we are not done yet. For example, if \(X=\mathbf{R}\) and we're quotienting by \(\mathbf{Z}\) as before, suppose that \(U\) is the interval \((1/3,2/3)\). The image \(q(U)\) under the quotient map to \(\mathbf{R}/\mathbf{Z}=S^1\) is the arc of circle between angles \(2\pi/3\) and \(4\pi/3\). The preimage \(q^{-1}(q(U))\) is the union of all intervals \((n+1/3,n+2/3)\) as \(n\) ranges over \(\mathbf{Z}\).

(19.44) To identify \(q^{-1}(q(U))\), observe that if \(x\in q^{-1}(q(U))\) then \(gx\in U\) for some \(g\in G\). For example, in the example we just described, \(q^{-1}(q(U))\) is the union of all translates of \(U\) under the group action. So \[q^{-1}(q(U))=\bigcup_{g\in G}g(U),\] which is a union of open sets (because \(g\) acts as a homeomorphism so \(g(U)\) is open) and is therefore open.
(21.50) We really used the group action here: in general a quotient map will not be open unless there is a good reason for it (like a group action). The lemma we just proved, which it may seem like a technicality now, will be useful when we come to study covering spaces.
Pre-class questions
Consider the blue space in the figure below (comprising four arcs). This has a \(\mathbf{Z}/2\)-action which rotates the space by 180 degrees. What is the quotient, (a), (b), or (c)? It also has a \(\mathbf{Z}/2\) action which reflects in the vertical axis: what is the quotient in that case, (a), (b), or (c)?

(a)
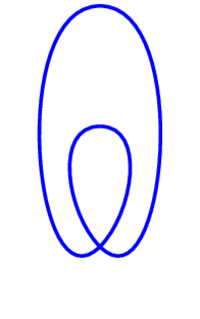 (b)
(b)
 (c)
(c)

- Let \(X=\{0,1,2\}\) with the topology \(\{\emptyset,\{0\},\{0,1\},\{0,1,2\}\}\). Consider the quotient \(X/\{0,2\}\). Show that \(X/\{0,2\}\) has the indiscrete topology and that the quotient map \(X\to X/\{0,2\}\) is not an open map (so we really did need the group action to prove our lemma).
Navigation
- Previous video: 3.02 Quotient topology: continuous maps.
- Index of all lectures.