3.01 Quotient topology
Video
Below the video you will find accompanying notes and some pre-class questions.
- Next video: 3.02 Quotient topology: continuous maps.
- Index of all lectures.
Notes
Quotient topology
(0.00) In this section, we will introduce a new way of constructing topological spaces called the quotient construction. This is intended to formalise pictures like the familiar picture of the 2-torus as a square with its opposite sides identified.
(0.29) Mathematically, the square is a subset of the plane and specifying the identification of opposite sides means giving an equivalence relation on this set.
(1.47) Given a space \(X\) and an equivalence relation \(\sim\) on \(X\), the quotient set \(X/\sim\) (the set of equivalence classes) inherits a topology called the quotient topology. Let \(q\colon X\to X/\sim\) be the quotient map sending a point \(x\) to its equivalence class \([x]\); the quotient topology is defined to be the most refined topology on \(X/\sim\) (i.e. the one with the largest number of open sets) for which \(q\) is continuous.
(3.20) If you try to add too many open sets to the quotient topology, their preimages under \(q\) may fail to be open, so the quotient map will fail to be continuous. More concretely, a subset \(U\subset X/\sim\) is open in the quotient topology if and only if \(q^{-1}(U)\subset X\) is open.
(4.40) There is a ``most refined topology for which \(q\) is continuous'', equivalently the collection of subsets \(U\) for which \(q^{-1}(U)\) is open forms a topology.
(5.00) The empty set is open: its preimage is the empty set which is open in \(X\).
The whole space \(X/\sim\) is open: its preimage is the whole space \(X\), which is open in \(X\).
(5.57) The preimage of a union is the union of the preimages, so if \(\mathcal{U}\) is a collection of open sets in \(X/\sim\) then \(\bigcup_{U\in \mathcal{U}}U\) is open because its preimage under \(q\) is \(\bigcup_{U\in\mathcal{U}}q^{-1}(U)\), which is a union of open sets in \(X\).
(6.47) The preimage of an intersection is the intersection of the preimages, so similarly the quotient topology allows finite intersections of open sets.
Examples
(7.18) I want to give you some examples which indicate why this definition captures the intuitive idea we have of forming a topological space by making identifications.
(7.39) Let \(X=[0,1]\) and let \(\sim\) be the equivalence relation which has as equivalence classes singleton sets \(\{x\}\) for \(x\in (0,1)\) and the set \(\{0,1\}\). The quotient space should be the circle, where we have identified the endpoints of the interval. Indeed, we can map \(X\) to the unit circle \(S^1\subset \mathbf{C}\) via the map \(q(x)=e^{2\pi ix}\): this map takes \(0\) and \(1\) to \(1\in S^1\) and is bijective elsewhere, so it is true that \(S^1\) is the set-theoretic quotient. We want to see that the usual topology on the circle is the quotient topology. Here are some open sets in \(S^1\) and their preimages under \(q\):
- (9.32) If I take an arc in \(S^1\) which does not pass through the point \(1\in S^1\) then its preimage is an interval in \((0,1)\). The arc in the circle (in the subspace topology coming from \(\mathbf{C}\) is open if and only if it is obtained by intersecting the circle with an open ball; in particular, it doesn't contain its endpoints. Similarly, the interval in \((0,1)\) is open if and only if it doesn't contain its endpoints, so at least for these arcs in \(S^1\setminus\{1\}\) we see that the arc is open if and only if its \(q\)-preimage is open.
- (10.24) If I take an arc in \(S^1\) which does pass through \(1\in S^1\) then its preimage is a pair of intervals \([0,a\}\cup\{b,1]\), which is open in the subspace topology on \([0,1]\subset\mathbf{R}\) if and only if the brackets \(\{,\}\) are open brackets (the fact that the endpoints \(0\) and \(1\) are included does not stop it from being an open set: remember that \([0,1]\) is an open set in \([0,1]\)!). These brackets are open if and only if the arc in \(S^1\) does not contain its endpoints, if and only if it is open in the subspace topology on \(S^1\).
(11.13) The quotient space is therefore making formal the notion that when you walk off the end of the interval, you come back at the other end: the preimage of an open set which crosses the point \(1\) is a pair of open sets at either end of the interval.
(11.39) Let \(S=[0,1]\times[0,1]\) be the square in \(\mathbf{R}^2\) and let \(\sim\) be the equivalence relation which identifies opposite sides (red with red, blue with blue in the figure below). We know this is supposed to be the 2-torus:
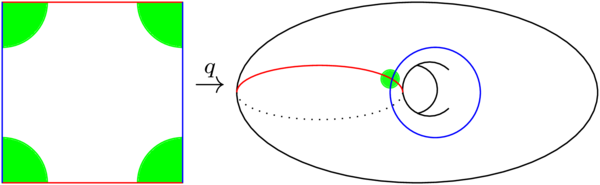
What is the preimage of the open green disc in the torus? It is a collection of four green quarter-discs at the corners of the square. This is open in the subspace topology on the square.
(13.09) What happens if I take one of these quarter discs and look at its image in the torus? Clearly from looking at the picture, this should not give me an open set: the quarter disc includes the two closed intervals where it intersects the boundary of the square, which is fine when considered in the subspace topology on the square, but we don't want an open subset of the torus to look like a quarter-disc which is open along its curved edge and closed on its two straight edges.
(13.52) The quotient topology fixes this for us. The preimage of this quarter-disc \(V\)in the torus certainly contains the quarter-disc in the square. But it also contains:
- two further intervals which are identified with sides of the quarter-disc under the equivalence relation,
- the remaining vertex of the square, which is identified with the centre of the quarter-disc under the equivalence relation.
That is definitely not an open set in the square, so \(q^{-1}(V)\) is not open, so \(V\) is not open.
(15.15) Take an octagon with side identifications as in the figure (ignore the horizontal purple line for now):
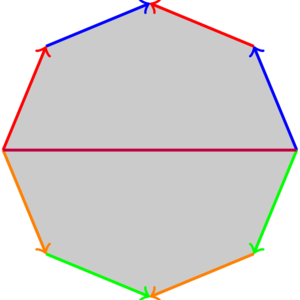
The quotient space turns out to be a surface of genus 2:

You can understand this as follows: the purple line in the diagram becomes a circle in the quotient which slices the surface into two punctured tori; each half of the octagon is (topologically) a square (with the side identifications for the torus) with a puncture.
(17.07) More generally, you can take a quotient of a \(4g\)-gon to get a genus \(g\) surface.
Crushing a subspace to a point
(17.30) Let \(X\) be a space and \(A\subset X\) be a subspace. Let \(\sim\) be the equivalence relation whose equivalence classes are \(A\) and \(\{x\}\) for \(x\not\in A\). The quotient space \(X/\sim\) is usually written \(X/A\): we think of this as the space obtained from \(X\) by crushing \(A\) down to a single point.
If \(X=[0,1]\) and \(A=\{0,1\}\) then \(X/A=S^1\).
(19.07) If \(X=D^2\) is the 2-disc and \(A=\partial D^2\) (the boundary circle) then \(X/A=S^2\) (if we think of the centre of the disc as the North Pole then all the points in \(A\) are identified to get the South Pole.
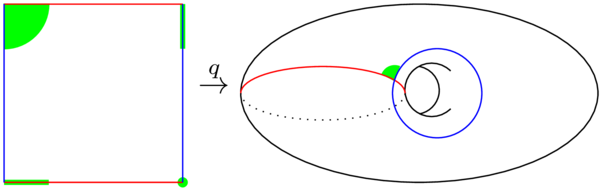
(20.12) Let \(X=S^1\times S^1\) be the 2-torus and let \(A=S^1\times\{pt\}\) be a meridian circle on the torus (the red circle in the figure). The quotient \(X/A\) is a pinched torus: see the figure below.

Pre-class questions
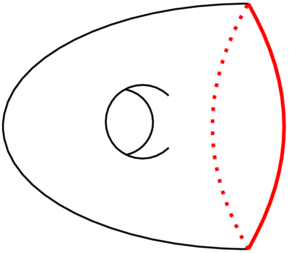
Let \(X\) be the space in the figure below and let \(A\) be the red subset. What is the topological space \(X/A\)?
Navigation
- Next video: 3.02 Quotient topology: continuous maps.
- Index of all lectures.