6.03 Braids: the Wirtinger presentation
Video
Below the video you will find notes and some pre-class questions. Once again, sorry for the gurgling background noises: I can't turn off my office radiator.
- Previous video: 6.02 Braids: Artin action.
- Index of all lectures.
Notes
(0.00) Let \(B\) be an \(n\)-strand braid inside \(D^2\times[0,1]\). If we take the quotient space \(D^2\times S^1=(D^2\times[0,1])/\sim\), \((x,0)\sim(x,1)\), then the braid closes up to become a collection of embedded circles \(C_B\) in \(D^2\times S^1\) (because the component paths \(B_k(t)\) start and end in the set of points \(z_1,\ldots,z_n\)). This is called the braid closure \(C_B\) of \(B\).
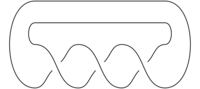
Here is an example: the braid closure of the 2-strand braid \(\sigma_1^3\) is the trefoil knot:
(1.59) Let \(X_B=(D^2\times S^1)\setminus C_B\) denote the complement of \(C_B\subset D^2\times S^1\). Let \(x=[1,0]\in(D^2\times[0,1])/\sim\) (we are thinking of \(D^2\subset\mathbf{C}\), so \(1\in D^2\) makes sense). We have
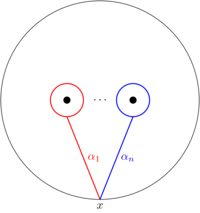
\begin{equation} \label{eq:knotcomp1} \pi_1(X_B,x)=\langle\alpha_1,\ldots,\alpha_n,g\ |\ g\alpha_kg^{-1} =B(\alpha_k)\mbox{ for }k=1,\ldots,n\rangle. \end{equation}Here, \(g\) is the loop \(x\times S^1\) and, for \(k\in\{1,\ldots,n\}\), \(\alpha_k\) is the element of \(\pi_1(D^2\setminus\{z_1,\ldots,z_n\}\) given by the loop in the figure below and \(B(\alpha_k)\) denotes the Artin action of \(B\) on \(\alpha_k\in\pi_1(D^2\setminus\{z_1,\ldots,z_n\}\cong\mathbf{Z}^{\star n}\).
(3.01) The space \(X_B\) is the mapping torus of the homeomorphism \[Art_B\colon D^2\setminus\{z_1,\ldots,z_n\}\to D^2\setminus\{z_1,\ldots,z_n\},\] so the lemma follows from the result we proved earlier which gave a presentation for the fundamental group of a mapping torus.
Consider the 2-strand braid \(\sigma_1\) (whose braid closure is an unknot). We have \[\sigma_1(\alpha)=\alpha\beta\alpha^{-1},\quad\sigma_1(\beta)=\alpha,\] so the presentation for \(\pi_1(X_{\sigma_1})\) is: \[\langle\alpha,\beta,g|g\alpha g^{-1}=\alpha\beta\alpha^{-1},g\beta g^{-1}=\alpha\rangle.\]
(8.44) If we embed \(D^2\times S^1\) as the standard solid torus in \(\mathbf{R}^3\) then the complement of the braid closure \(C_B\subset \mathbf{R}^3\) has
\begin{equation} \label{eq:knotcomp2} \pi_1(\mathbf{R}^3\setminus C_B)=\langle\alpha_1,\ldots,\alpha_k\ |\ \alpha_k=B(\alpha_k),\ k=1,\ldots,n\rangle \end{equation}where \(B(\alpha_k)\) is the Artin action of \(B\) on the free group \(\langle\alpha_1,\ldots,\alpha_k\rangle\).
(A homotopy retract of) the complement \(\mathbf{R}^3\setminus C_B\) is obtained from \(X_B\) by attaching a 2-cell along the circle \(x\times S^1\), which adds the relation \(x=1\) to the presentation from the lemma, yielding the desired presentation.
(11.26) Consider the 2-strand braid \(\sigma_1\) (whose braid closure is an unknot). We have \[\pi_1(X_{\sigma_1})=\langle\alpha,\beta,g|g\alpha g^{-1}=\alpha\beta\alpha^{-1},g\beta g^{-1}=\alpha\rangle\] so the Wirtinger presentation is obtained by setting \(g=1\): \[\langle\alpha,\beta|\alpha=\alpha\beta\alpha^{-1},\beta=\alpha\rangle.\] We can simplify this to just get \(\langle\alpha\rangle\), so the fundamental group is \(\mathbf{Z}\).
I said that this allows us to compute the fundamental group of any knot complement: this is because one can show that any knot is isotopic to a braid closure; a proof of this was first written down by Alexander (1923, ``A lemma on a system of knotted curves'') and it is quite readable.
Pre-class questions
- The video claimed that "any braid gives a knot by taking the braid closure". Why was this claim false? What should I have said instead?
Navigation
- Previous video: 6.02 Braids: Artin action.
- Index of all lectures.