6.02 Braids: Artin action
Video
Below the video you will some pre-class questions and notes to accompany the video. Apologies for the gurgling noises in the background of the video: it's my office radiator.
- Previous video: Braids: Introduction.
- Next video: Braids: the Wirtinger presentation.
- Index of all lectures.
Notes
The Artin action
(0.00) Recall from Braids 1 that the braid group on \(n\) strands is the fundamental group of the unordered configuration space \(UC_n\). This group acts on the group \(\mathbf{Z}^{\star n}\) via automorphisms; this action is called the Artin action of the braid group on the free group. In this section we will outline the reason for this; in the next section, we will compute explicitly the Artin action for some simple braids.
Monodromy
(2.30) Inside \(\mathbf{C}\times UC_n\) we have a tautological subspace \[T_n=\{(x,c)\ :\ x\in c\}\] which meets the disc \(\mathbf{C}\times\{c\}\) over a configuration \(c\in UC_n\) in the \(n\) points defining the configuration \(c\). Consider the complement of \(T_n\), that is \[U_n:=\left(\mathbf{C}\times UC_n\right)\setminus T_n.\] This is called the universal family over configuration space. The space \(U_n\) has a natural projection \[p\colon U_n\to UC_n\] whose fibre \(F_c=p^{-1}(c)\) over \(c\) is precisely the plane punctured along the configuration \(c\).
In a former version of this module, I had already introduced covering spaces before talking about the Artin action, so the following paragraph made \(\epsilon\)-more sense. If I were you, I would skip this paragraph on a first reading, read the section below where we do an example and then come back and re-read this paragraph when you've seen the videos on covering spaces and monodromy.
The universal family has a nice property: while it is not a covering space of the configuration space, it is a fibration over the configuration space. This means that if \(F\colon X\times [0,1]\to UC_n\) is a map and \(\tilde{F}_0\colon X\to U_n\) is a lift of \(F|_{X\times\{0\}}\) then there exists a (not necessarily unique) lift \(\tilde{F}\colon X\times [0,1]\to U_n\) of \(F\). In particular, given a path \(\gamma\) in \(UC_n\), we get a monodromy map from the fibre \(F_{\gamma(0)}\) to the fibre \(F_{\gamma(1)}\), which is well-defined up to homotopy. In particular, we get an action of \(\pi_1(UC_n,c)\) on \(\pi_1(F_c,[z_1,\ldots,z_n])\cong\mathbf{Z}^{\star n}\). This is called the Artin action of the braid group on the free group.
Explicit action
(5.40) Rather than proving the fibration property of the universal family, let us see how some explicit braids act in the Artin action. Hopefully the idea will become clear.
Let \(n=2\) and consider the elementary braid \(\sigma_1\). The fundamental group of \(\mathbf{C}\setminus\{z_1,z_2\}\) is \(\mathbf{Z}\star\mathbf{Z}\), with generators \(\alpha\) and \(\beta\) as drawn in the figure below.
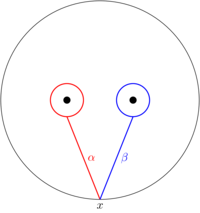
The braid \(\sigma_1\) moves the points \(z_1\) and \(z_2\) around one another until they switch places. The result on the loops \(\alpha\) and \(\beta\) is as follows:
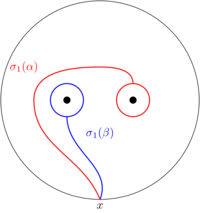
(9.04) We can see that \(\sigma_1(\beta)=\alpha\), and, after a homotopy, we can see that \(\sigma_1(\alpha)=\alpha\beta\alpha^{-1}\):

(11.16) Therefore we have
\begin{align*} \sigma_1(\alpha)&=\alpha\beta\alpha^{-1}\\ \sigma_1(\beta)&=\alpha \end{align*}(11.37) What about when we add more strands? In fact, if we focus just on elementary braids (which generate the braid group), we already know the answer: an elementary braid only affects two of the strands, and we can take the monodromy to be the identity away from these two strands. In other words, the action of \(\sigma_i\) on \(\alpha_1,\ldots,\alpha_n\) is:
\begin{align*} \alpha_1&\mapsto\alpha_1\\ \alpha_2&\mapsto\alpha_2\\ \vdots & \quad\vdots\\ \alpha_i&\mapsto\alpha_i\alpha_{i+1}\alpha_i^{-1}\\ \alpha_{i+1}&\mapsto\alpha_i\\ \vdots & \quad\vdots\\ \alpha_n&\mapsto\alpha_n. \end{align*}In the next video, we will use the Artin action to compute the fundamental group of any knot complement.
Pre-class questions
- What is the Artin action of \(\sigma_1^{-1}\)?
Navigation
- Previous video: Braids: Introduction.
- Next video: Braids: the Wirtinger presentation.
- Index of all lectures.