Super-cell generation

The next step is to construct a super-cell, this can be done using the following setting in the INPHON file:

LSUPER =.TRUE.      (default)
NDIM = NX NY NZ    (default: 1 1 1)
NTYPES = 1        (no default)

where NX, NY and NZ are positive integer numbers. NTYPES is the number of different atomic species (1 in this example). We shall start with a small super-cell, so set NX = NY = NZ = 2. Now run the phon code:

$>$ phon

The program has generated a file called SPOSCAR which contains the super-cell (8 atoms in this case). Now copy SPOSCAR to POSCAR.

$>$ cp SPOSCAR POSCAR

The program also prints out a guess for the displacements needed to construct the full force field. These are written on the stout (the screen) and in the file DISP. Because of the symmetries present in the FCC crystal, in this particular case only one displacement is needed. The size of the displacement is 0.04 Å by default, but of course we will need to make sure that this displacement is small enough for the system to still be in the harmonic limit. We will test this later. Now we need to displace the atom in the primitive cell according to the suggested displacement and calculate the forces on all the atoms in the unit cell using vasp. To start with, we will also use a rather coarse grid of k-points, so the calculations will be quick. Edit the KPOINTS file and specify a 2 2 2 grid. Then we need to run vasp and create the file FORCES, which contains the informations on the atom displaced, its displacement, and the forces on all the atoms in the super-cell. phon requires the forces to be in units of eV/Å, which are the units already provided by vasp. The above steps are automatically performed by the script runphon. All we need to do is to modify the script to provide the displacement.

$>$ runphon

After the script has run you will find a newly created FORCES file, which now can be used by phon to calculate phonon frequencies. The first thing we are going to do is to calculate phonons dispersions along some special directions in the BZ and compare them with experimental data (provided in the file EXPAL). To do this, we have to set the following in the INPHON file:

LSUPER = .FALSE.
MASS = 26.98         Mass of the Al atom in amu units
LRECIP = .F.                 Special q-points in cartesian coordinates
ND = 3                         3 different special directions in the BZ
NPOINTS = 51              51 points between any two special q-points
QI = 0.0 0.0 0.0      1.0 1.0 0.0      0.0 0.0 0.0      3 initial special q-points
QF = 1.0 0.0 0.0      0.0 0.0 0.0      0.5 0.5 0.5      3 final special q-points

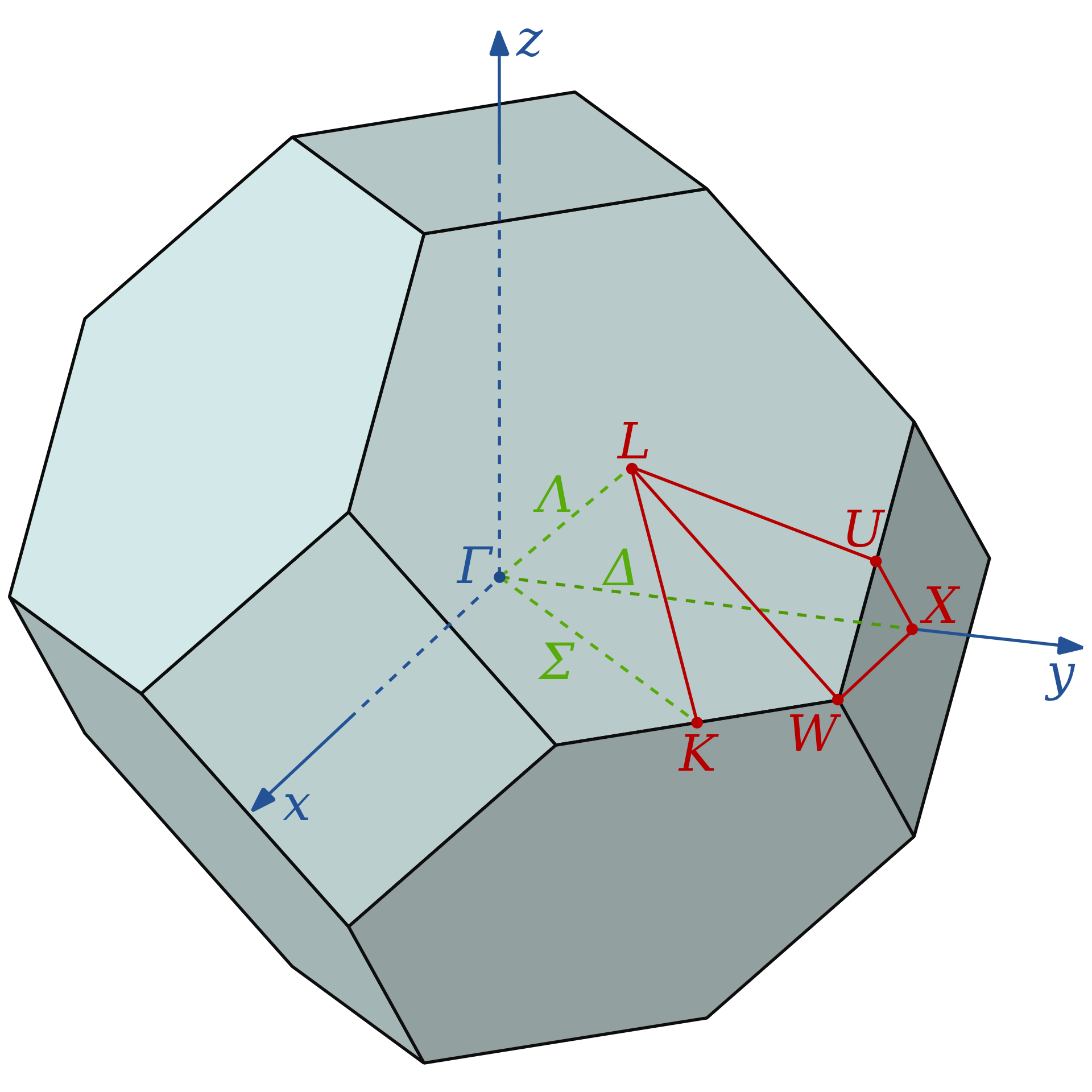
with these setting phon will calculate phonon frequencies at 51 points along three different special directions in the BZ, defined by the three initial (QI) and the three final (QF) q-points. The first direction is defined by QI=(0.0,0.0,0.0) ($\Gamma$) and QF=(1.0,0.0,0.0) (called X), and is called $\Delta$ (see Fig. ).

Figure: The Brillouin zone of the FCC lattice. Note that X and L are zone boundary points, i.e. half way between two reciprocal lattice points.

The second direction is defined by QI=(1.0,1.0,0.0) and QF=(0.0,0.0,0.0) and is called $\Sigma$. Note that (1.0,1.0,0.0) is equivalent to (1.0,0.0,0.0), so the initial and the final points of this second direction are the same as those of the previous direction, with the QI and QF swapped, however, the direction is different, as this second one also goes through the point K = (0.75,0.75,0.0). The third and final direction has QI=(0.0,0.0,0.0) and QF=(0.5,0.5,0.5) (called L), and is called $\Lambda$. The phonon frequencies are written in the file FREQ.cm, which we can now plot (for example using gnuplot) together with the experimental frequencies contained in the file EXPAL ^9.4. You can use the file f.g for convenience, edit this appropriately and then type:

$>$ gnuplot

gnuplot$>$ load 'f.g'

You can see that the agreement with the experimental phonons is only fair. There are at least two reasons for this. The first is that the calculated phonons are only exact at q-vectors compatible with the super-cell, and the rest represent an interpolation in the BZ. However, we know that a $2 \times 2 \times 2$ supercell must give exact phonons at zone boundary, the (1.0,0.0,0.0) point for example, and they do not seem to be very accurate at that point. This is related to the second reason, and namely that the DFT calculations are not accurate enough as our grid of k-points is not dense enough.