5.02 Fundamental group of a CW complex
Video
Below the video you will find accompanying notes and some pre-class questions.
- Previous video: Van Kampen's theorem.
- Next video: Fundamental group of a mapping torus.
- Index of all lectures.
Notes
Example of the 2-torus revisited
(0.00) In the previous video, we saw how to use Van Kampen's theorem to compute the fundamental group of the 2-torus. The result was \[\langle a,b\ |\ b^{-1}a^{-1}ba=1\rangle.\] There is a CW structure on the 2-torus (square with opposite sides identified) with one 0-cell (vertex), two 1-cells (edges) and one 2-cell (the square itself). It is no coincidence that the presentation we obtained has:
- one generator for each 1-cell,
- one relation for each 2-cell: the relation comes from looking at the boundary of the 2-cell.
Fundamental group of a CW complex
(1.24) If \(X\) is a CW complex with one 0-cell (for simplicity) then \(\pi_1(X)\) has a presentation where the generators are the 1-cells and the relations come from the 2-cells. More precisely,
- each 1-cell is a loop (as both ends attach to the unique 0-cell). These loops generate \(\pi_1(X)\);
- (3.05) the boundary of each 2-cell \(e\) gives a loop \(\partial e\) in the 1-skeleton which we can write as a word in the 1-cells; since this loop is nullhomotopic in \(e\) we need the relation \(\partial e=1\) in \(\pi_1(X)\). These relations suffice to give a presentation of \(\pi_1(X)\).
(5.18) Note that this theorem is about cell complexes of any dimension; in other words, the 3-cells, 4-cells, etc. do not affect the fundamental group.
(5.38) Let \(X^1\) be the 1-skeleton of \(X\). This is obtained by attaching 1-cells to a point, so \(X^1\) is just a wedge of 1-cells \(X^1=\bigvee_{1\mbox{-cells}}S^1\). By induction, using the computation from last time, \(\pi_1(X^1)=\bigstar_{1\mbox{-cells}}\mathbf{Z}\) (i.e. the free product of copies of the integers, one for each 1-cell, in other words, the group with one generator for each 1-cell and no relations).
(7.42) What happens when we attach a 2-cell?
Claim: If \(Y\) is any space and \(Z\) is obtained from \(Y\) by attaching a 2-cell \(e\) with some attaching map \(\varphi\) then \(\pi_1(Z)=\pi_1(Y)/N(\partial e)\), where \(N(\partial e)\) is the normal subgroup generated by the boundary of \(e\) (that is \([\varphi]\in\pi_1(Y)\)). This is equivalent to imposing the relation \(\partial e=1\).
(9.48) Proof of claim: This follows from Van Kampen's theorem. If we decompose \(Z=U\cup V\) where \(U\) is the interior of the 2-cell \(int(e)\) and \(V\) is the union \(Y\cup (e\setminus\{0\})\) (that is, \(V\) is everything except one point in the interior of \(e\)).
- The intersection \(U\cap V\) is \(e\setminus\{0\}\), the punctured 2-cell. That is homotopy-equivalent to a circle.
- \(U\) is contractible.
- \(V\) is homotopy equivalent to \(Y\) (retracting the punctured 2-cell down onto its boundary in \(Y\)).
(11.45) Van Kampen's theorem tells us that \(\pi_1(Z)=\pi_1(Y)\star_{\mathbf{Z}}\{1\}\). In other words, we take \(\pi_1(Y)\) and we add an amalgamated relation \(\partial e=1\) (\(\partial e\) generates \(\pi_1(U\cap V)\): in \(\pi_1(U)\) is becomes trivial and in \(\pi_1(V)\) it becomes \(\partial e\)).
(13.28) What about adding higher dimensional cells? By the same argument, where \(e\) is an \(n\)-cell with \(n>2\), we get \[\pi_1(Z)=\pi_1(Y)\star_{\{1\}}\{1\},\] because \(U\cap V\) is now homotopy equivalent to the \((n-1)\)-sphere, which is simply-connected (so there is no new amalgamated relation).
Pre-class questions
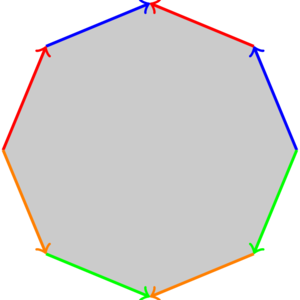
Given that the quotient of the octagon by the identifications indicated in the figure below is a genus 2 surface, use Van Kampen's theorem to give a presentation for the fundamental group of a genus 2 surface.
Navigation
- Previous video: Van Kampen's theorem.
- Next video: Fundamental group of a mapping torus.
- Index of all lectures.