1.09 Homotopy equivalence
Video
Below the video you will find accompanying notes and some pre-class questions.
- Previous video: 1.08 Brouwer's fixed point theorem.
- Next video: 1.10 Homotopy invariance.
- Index of all lectures.
Notes
(0.00) In this section, we will define a notion of homotopy equivalence of spaces, which you should think of as saying two spaces can be deformed into one another; for example, the symbols θ and 8 are homotopy equivalent (just by contracting the contractible bar midway up the θ). The fundamental group is a homotopy invariant, and we will eventually be able to compute it simply by looking at a space, and noticing that it's homotopy equivalent to a simpler space whose fundamental group we already know.
Homotopy of maps
(1.23) We first need the notion of homotopy of maps.
Let \(X,Y\) be spaces. Two continuous maps \(F,G\colon X\to Y\) are homotopic if there is a continuous homotopy \(H\colon X\times[0,1]\to Y\) such that \(H(x,0)=F(x)\) and \(H(x,1)=G(x)\) for all \(x\in X\). We write \(F\simeq G\).
(2.57) When \(X=S^1\), this coincides with the notion of free homotopy of loops. In general, we will think of this as a one-parameter family of maps \(F_s\colon X\to Y\) (where \(F_s(x)=H(x,s)\)) interpolating between \(F_0=F\) and \(F_1=G\).
(4.13) The analogue of a based homotopy is the following.
Let \(X,Y\) be spaces and let \(A\subset X\) be a subset. Two continuous maps \(F,G\colon X\to Y\) satisfying \(F|_A=G|_A\) are homotopic rel \(A\) if there is a homotopy \(H\colon X\times[0,1]\to Y\) such that \(H(x,0)=F(x)\) and \(H(x,1)=G(x)\) for all \(x\in X\) and \(H(x,s)\) is independent of \(s\) for all \(x\in A\).
This gives based homotopy (or homotopy with fixed endpoints) if \(A=\{0,1\}\subset[0,1]=X\).
Contractible spaces
(5.40) Let \(X=Y=\mathbf{R}^n\), let \(F\colon\mathbf{R}^n\to\mathbf{R}^n\) be the identity map \(F(x)=x\), and let \(G\colon\mathbf{R}^n\to\mathbf{R}^n\) be the constant map \(G(x)=0\). Then \(F\simeq G\) via the homotopy \(H(x,s)=sx\).
(7.19) A space \(X\) is contractible if the identity map \(id_X\) is homotopic to a constant map. A homotopy from the identity to a constant map is called a nullhomotopy. The previous example shows that \(\mathbf{R}^n\) is contractible.
Homotopy equivalence
(8.55) A map \(F\colon X\to Y\) is a homotopy equivalence if there exists a map \(G\colon Y\to X\) such that \(F\circ G\simeq id_Y\) and \(G\circ F\simeq id_X\). We say that \(G\) is a homotopy inverse for \(F\) (note that \(F\) does not need to be invertible).
(11.08) If there exists a homotopy equivalence \(F\colon X\to Y\), we say that \(X\) and \(Y\) are homotopy equivalent and we write \(X\simeq Y\).
(11.44) A contractible space \(X\) is homotopy equivalent to a point \(\{p\}\).
Let \(F\colon X\to \{p\}\) be the constant map \(F(x)=p\) and let \(G\colon \{p\}\to X\) be the inclusion of a point \(G(p)=x_0\). We have \[F\circ G(p)=F(x_0)=p,\quad\Rightarrow\quad F\circ G=id_{\{p\}},\] and \[G\circ F(x)=G(p)=x_0,\quad\Rightarrow\quad G\circ F=\mbox{const}.\] Since \(X\) is contractible, \(G\circ F\) is homotopic to the identity on \(X\).
Examples
(14.56) In the next section, we will see that homotopy equivalent spaces have isomorphic fundamental groups. For the rest of this section, we will look at examples of homotopy equivalent spaces.
(15.24) Let \(Y\) be the following (grey) subset of the plane:
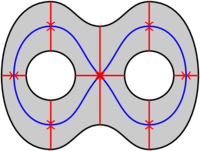
and let \(X\) be the blue figure 8 (drawn as a subset of \(Y\)). Then \(X\simeq Y\). Let \(G\colon Y\to X\) be the map which projects along the red arrows in the figure and let \(F\colon X\to Y\) be the inclusion map. Then \(G\circ F\) is the identity and \(F\circ G\) is homotopic to the identity: a homotopy from the identity to \(F\circ G\) can be obtained by flowing along the red arrows (i.e. \(H(x,s)\) is the point you get from \(x\) by moving a fraction \(s\) along the red arrow through \(x\) towards the figure 8).
(18.21) Let \(B\) be the unit ball in \(\mathbf{R}^3\) and let \(C\) be a small tubular neighbourhood of the \(x\)-axis. Let \(X=B\setminus C\). Then \(X\) is homotopy equivalent to the circle (you can see it by imagining the circle sitting in the \(yz\)-plane at radius \(1/2\) (so inside \(X\)) and ``squishing'' \(X\) down onto this core circle by following arrows in much the same way as the previous example.
(19.47) Some examples you might like to think about:
- \(\mathbf{R}^3\setminus K\) where \(K\) is a neighbourhood of the unit circle in the \((z=0)\)-plane.
- \(\mathbf{R}^3\setminus (K_{-1}\cup K_1)\), where \(K_j\) is a neighbourhood of the unit circle in the plane \(z=j\), \(j=\pm 1\).
Pre-class questions
- How many homotopy equivalence classes of symbols are there in the following list? ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789
- Show that homotopy equivalence of spaces is an equivalence relation.
Navigation
- Previous video: 1.08 Brouwer's fixed point theorem.
- Next video: 1.10 Homotopy invariance.
- Index of all lectures.