7.03 Path-lifting: uniqueness
Video
Below the video you will find accompanying notes and some pre-class questions.
- Previous video: 7.02 Path-lifting, monodromy.
- Next video: 7.04 Homotopy-lifting, monodromy.
- Index of all lectures.
Notes
(0.00) In the last section, we saw that if you have a path \(\gamma\) in \(X\) starting at \(x=\gamma(0)\), a covering space \(p\colon Y\to X\) and a point \(y\in p^{-1}(x)\) then there exists a lifted path \(\tilde{\gamma}\) in \(Y\) with \(\tilde{\gamma}(0)=y\). In this section, we will see that this lift is unique.
Uniqueness of lifts
(1.00) We will prove the following, more general, result.
Let \(p\colon Y\to X\) be a covering space. Let \(T\) be a connected space. Let \(F\colon T\to X\) be a continuous map. Then two lifts \(\tilde{F}_1,\tilde{F}_2\colon T\to Y\) are equal for all \(t\in T\) if and only if they are equal for some \(t\in T\).
(2.35) For path lifting, \(T=[0,1]\) and \(F=\gamma\); the lemma will imply that two lifts which agree at \(0\in[0,1]\) agree everywhere.
(2.49) Recall that \(\tilde{F}\) is a lift if \(p\circ\tilde{F}=F\).
(3.14) We need to prove that if \(\tilde{F}_1(t)=\tilde{F}_2(t)\) for some \(t\in T\) then \(\tilde{F}_1(t)=\tilde{F}_2(t)\) for all \(t\in T\).
Let \(S=\{t\in T\ :\ \tilde{F}_1(t)=\tilde{F}_2(t)\}\). We need to prove that \(S\) is open and that \(T\setminus S\) is open (i.e. \(S\) is closed). Since \(T\) is connected, this implies that either \(S=\emptyset\) or \(T\setminus S=\emptyset\), so if \(S\) is nonempty then \(S=T\) and \(\tilde{F}_1\equiv\tilde{F}_2\).
(5.22) Given a point \(t\in T\) and let \(x=F(t)\). Since \(p\colon Y\to X\) is a covering space, there is an elementary neighourhood \(W\subset X\) of \(x\). In \(Y\) there are elementary sheets \(V_1\) and \(V_2\), projecting to \(W\), containing \(\tilde{F}_1(t)\) and \(\tilde{F}_2(t)\) respectively.
(7.32) Since \(\tilde{F}_1,\tilde{F}_2\) are continuous, there exist open sets \(U_1,U_2\subset T\) such that \(t\in U_i\) and \(\tilde{F}_1(U_i)\subset V_i\) for \(i=1,2\). Let \(U=U_1\cap U_2\).
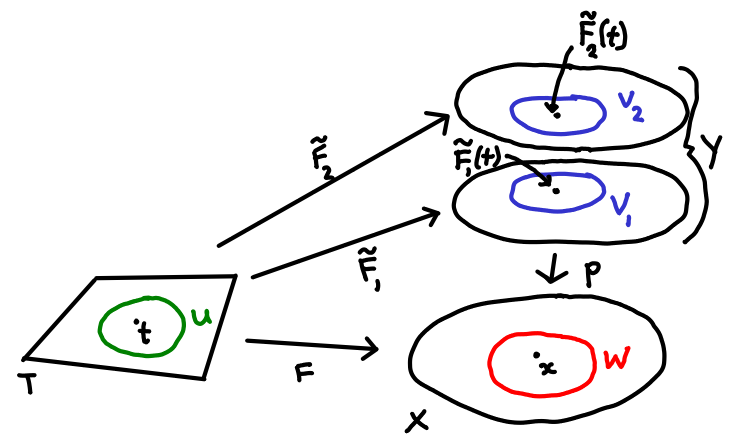
(8.45) We want to show that \(T\setminus S\) is open, so suppose that \(t\in T\setminus S\). Then I claim that \(U\subset T\setminus S\), which will prove that every point in \(T\setminus S\) has an open neighbourhood contained in \(T\setminus S\), which implies that \(T\setminus S\) is open.
(9.40) The claim can be proved as follows. Since \(t\in T\setminus S\), \(\tilde{F}_1(t)\neq\tilde{F}_2(t)\), so \(V_1\) and \(V_2\) are disjoint. Therefore \(\tilde{F}_1(t')\neq\tilde{F}_2(t')\) for all \(t'\in U\) (because \(t'\in U\) implies \(\tilde{F}_1(t')\in V_1\) and \(\tilde{F}_2(t')\in V_2\), and \(V_1\cap V_2=\emptyset\)).
(11.25) We also want to show that \(S\) is open, so suppose that \(t\in S\). Then \(\tilde{F}_1(t)=\tilde{F}_2(t)\), so \(V_1=V_2=:V\). There exists a local inverse \(q\colon W\to V\) to \(p\), i.e. \(p\circ q=id_W\), \(q\circ p=id_V\).
(12.53) If \(t'\in U\) then \(\tilde{F}_1(t')\in V\) and \(\tilde{F}_2(t')\in V\), so \(q(F(t'))=q(p(\tilde{F}_1(t')))=\tilde{F}_1(t')\) and \(q(F(t'))=q(p(\tilde{F}_2(t')))=\tilde{F}_2(t')\), so we deduce that \(\tilde{F}_1(t')=\tilde{F}_2(t')\). Therefore \(\tilde{F}_1\) and \(\tilde{F}_2\) agree on \(U\), which proves that \(S\) is open.
This proves the lemma.
Pre-class questions
- There is a condition on covering spaces which I'm using in this section but which I forgot to mention in earlier sections. Can you spot what it is?
Navigation
- Previous video: 7.02 Path-lifting, monodromy.
- Next video: 7.04 Homotopy-lifting, monodromy.
- Index of all lectures.