by Ted Honderich
-- Determinism and Freedom Philosophy Website --
This is an account of the fundamental connection between an effect, say the windshield wipers starting to work in this Citroen car, and what precedes it. What precedes it, fundamentally, is a causal circumstance or causally sufficient condition. This includes a number of conditions, one of them usually called the cause of the effect, say flipping the switch. The account below of the fundamental lawlike or 'whatever-else' connection between a causal circumstance and its effect is the third section of a chapter of a book, the first two sections being about what causes and conditions are -- individual properties -- and about four unfundamental connections between the effect and the cause and other conditions. One of the unfundamental connections is that if the cause hadn't happened, the effect wouldn't have happened either -- the cause was required for the effect.
The account below rejects Hume's temptingly simple idea of the fifth connection, between causal circumstance and effect, that it is just that all things like the first are followed by things like the second. It also looks directly at the subject-matter rather than approach it by way of some enthusiasm or specialism, as some philosophers are inclined to to. You need to concentrate to get the message, but there is no mystery in it.
1.3 'IF A, EVEN IF X, THEN STILL B'
The fifth connection is different. To approach it informally, suppose
that we spend time and arrive at a thorough understanding of the
ordinary operation of this Citroen's windscreen wipers. We come to
believe that whenever ten specified types of conditions obtain,
including a flipping of the switch, there is the effect of the wipers'
starting to work. What do we believe if on a certain occasion we have
taken it that there exist conditions of exactly the ten types, including a
flipping, but the wipers do not start? We may suppose that we are
mistaken on this occasion in taking it that all the ten types of
conditions do obtain. We may suppose, differently, that our prior
thorough understanding of the ordinary operation of the wipers was
not thorough enough. That is, there is an additional type of condition
which obtains when the wipers start—not ten in all but eleven. More
likely, we may suppose that we have not arrived at an exact
specification of one or more of the ten. What is needed is not exactly a
particular type of condition specified before the present occasion, but a
slightly different one, which did indeed obtain previously when the
wipers started.
What is common to these and related responses is that if we take the
starting of the wipers to be an effect we believe at least that there is
some type of circumstance which is uniformly connected with the
wipers' starting. Whenever a circumstance of this kind exists, there
also occurs a starting-to-work of the wipers. Certainly we do take any
standard effect to be an instance of such a uniform connection.
However, is this all that there is in the world, along these lines, to the
connections between an effect and its causal circumstance?
Hume gave one of philosophy's most famous answers, an answer
whose strength is owed to its great clarity and simplicity, when he said
yes. (1888 (1739), pp. 73 ff.) To give the answer is to refuse to go far
beyond what we already have, or have as implied, in connection (4). If
the answer leads very naturally to the truth, it is nevertheless
mistaken, as is shown by the philosophically familiar but evergreen
fact that certain items constitute an instance of such a uniform
connection or constant conjunction, but the second is not the effect of
the first. Although each causal circumstance and effect, likewise, is an
instance of such a uniform connection, that is not its unique nature.
Consider a particular day and the night that follows. The example is
of course that of Hume's early critic Thomas Reid (1969 (1788) ), and
has many counterparts, some of them being members of runs of total
coincidences. Let us have in mind, only slightly less imprecisely, a
period of light in London and thereabouts, that one I now call
yesterday, and a following period of darkness, last night. We could of
course give precise spatio-temporal specifications. It seems that if any
two things whatever satisfy the Humean requirement, yesterday and
last night do—all days are followed by nights. But yesterday and last
night, however they are related, are not related as causal circumstance
and effect. Yesterday did not cause last night. More must be true of any
different pair of things which in fact are causal circumstance and
effect.
There have been many attempts to save the Humean account, or
some development of it. (Ayer, 1940, pp. 179 f.; Hempel and Oppen-
heim, 1953, pp.337ff.; Nagel, 1979, pp.64f.,- Berofsky, 1971,
pp. 203 f.; cf. Earman, 1986, Ch. 5; Honderich, 1991) They cannot but
strike one as unsuccessful, partly because ad hoc. The Humean view
has persisted, among all those disinclined to mystery in connection
with causation, not because of these defences, but for want of a
satisfactory alternative. The alternatives have for the most part
consisted in elusive doctrines of 'natural necessity', causal 'power',
'agency' or some kind of 'logical connection' and in inexplicit
declarations of the reality of causal necessitation. Now there are
superior alternatives, not at all of the unsatisfactory kinds. One of
them, to my mind, gives an unfanciful, clear, and true view of the
relation between causal circumstance and effect. This alternative
view, a member of a small family of related although differing views,
follows on naturally enough from a consideration of Hume's.
Why do we not take yesterday as the causal circumstance for last
night? What do we take to be the difference between yesterday and last
night, on the one hand, and, on the other, another instance of constant
conjunction, the one comprising the true causal circumstance and last
night? It is that we might, in other than merely a logical sense, have
got yesterday but not last night. Certain other events or conditions might
have occurred such that we got yesterday but not last night.
One would have been the creation of a new light source, about as great
as the sun. It is thus false that if certain other things had happened,
although we got yesterday, we would still have got last night.
Compare what we take to be the true causal circumstance for last
night, which we may label the solar conditions. They included,
roughly speaking, the earth's London face being away from the sun for
a time, the absence of any light source like that of the sun, in the right
place at the right time, and conditions having to do with the behaviour
of light. It is not true that certain other events or conditions might
have occurred such that we got the solar conditions but not last night.
If or since we had the solar conditions, even if certain other things had
happened, we would still have got last night. This is indeed what
distinguishes causal circumstances and effects (and nomic correlates)
from other instances of constant conjunction. This, if it needs to be
made more precise, is what we need to concentrate on, as some others
have before, although without coming to the conclusion we shall
reach. (Mill, 1961 (1843), Bk. 3, Ch. 5, s. 6; Ayer, 1963, 1963a, pp. 231-
4; Goodman, 1954; Hospers, 1956; Downing, 1958-9, 1959, 1970;
Honderich, 1981b, pp. 421 f., 1982a, pp. 302-3)
Let us take the variable x to cover or range over certain conceivable
events or conditions or whatever—in fact individual properties or sets
of them—which in fact did not occur. They are, we can as well say,
certain conceivable changes in the universe, ways in which the
universe might have been different. Let us contemplate, first, that they
include all such changes save for the absence of cc or of e. They include
all such changes save for logical excluders of cc or e. We can now
contemplate that the relevant cc-e connection, when we suppose that
cc caused e, can be stated in this way: If cc occurred, then even if x had
occurred, e would still have occurred. That is on the right lines, of
course, since certainly we do not suppose that e would have occurred
even if either cc or e itself did not. However, it will not do. We
regularly take it that a causal circumstance is linked by way of a causal
chain or sequence to its effect. Without attempting a characterization
of such sequences, let us suppose that a link k occurred in a causal
sequence connecting cc with e. Clearly we do not believe that since cc
occurred, e would still have as it did, even if k had been missing. We
need to restrict x a bit more in order to express what we want.
What we come to is this. If cc was a causal circumstance for e, then
(5) If cc occurred, then even if there also occurred any change x
logically consistent with cc and e, it was never the less the case that
e occurred—or, cc began and e ended a sequence of things such that
it was true of each one and its immediate successor that if the first
occurred, even if there also occurred any change x logically
consistent with both, then the second also occurred. To speak
differently, if e had not occurred, then even if there had also occurred
any change x logically consistent with the absences of e and of cc,
and consistent with the absences of links between cc and e, it would
also have been the case that cc did not occur.
This fifth causal relation, like several to come, is stated by what we
can call independent nomic conditional statements, or simply inde-
pendent conditionals. Their truth, in brief, is independent of what else
is true. Expressed one way, as we generally shall, they are of the form If
a occurred, then even if any events or conditions logically consistent
with a and b had also occurred, in place of those which did, b would
still have occurred. Or, as we can as well say, Even if any events or
conditions logically consistent with a and b had occurred, rather than
those which did, if a occurred then b did. Or again, independent nomic
conditionals come to this: Given the rest of the world as it was, or
given that it was different in any way we can conceive it as being,
without logically excluding a and b, then if a happened so did b.
Independent conditional statements are thus different in kind from
those dependent nomic conditional statements or simply dependent
conditionals, which state the first four of our causal relations.
Dependent nomic conditionals are certain of the statements of the
form If a occurred, then b occurred. Their truth, in brief, is dependent
on what else is true.
By way of abbreviation of what is stated by the independent
conditionals in (5), cc can be said to have necessitated e, and e can be
said to have been necessary to cc. We can also, in abbreviation, speak
of an event as necessitated without identifying or indeed knowing its
causal circumstance. Here a necessitated event is of course to be
understood as an event which does stand in the given relation to some
or other antecedent. Like remarks might have been made elsewhere—
with respect to a required event, for example. What we have in (5)
might be improved in a number of ways so as to deal with questions
and indeed objections, and thereby complicated and indeed greatly
complicated. In particular the contrapositive formulation might be
considered further. What we have, further, might be expressed in
several different logical notations. We might consider problems (e.g.
Wiggins, 1973) and proposed solutions (e.g. Thorp, 1980, pp. 16-26)
which arise in connection with notations. What we have will suffice as
it stands. It does indeed distinguish yesterday and last night from the
other instance of constant conjunction, the solar conditions and last
night The solar conditions but not yesterday count as causal
circumstance for last mght. There is no peculiarity, incidentally, about
this particular very grand causal circumstance and effect. Reflection on
smaller examples of causal circumstance and effect, such as those with
which we began, is quite as capable of illustrating this fifth causal connection.
The given connection between causal circumstance and effect is in
factthe principal instance of what can be called fundamental nomic
connection or fundamental necessary connection. Such connection is
what is stated by independent nomic conditionals and, of course, holds
between any two things when it is true that if or since the first
occurred then even if any change logically consistent with either had
also occurred, the second would still have occurred. Fundamental
nomic connection, as will be made clearer, is just that -- fundamental.
It is the stuff of or the basis of all the relations specified so far or still to
be specified between cause and effect, causal circumstance and effect.
There are two more causal connections to be noted. As we saw
earlier (2) an ordinary causal circumstance is required for its effect. If,
say, the ten conditions including the flipping of the switch had not
occurred or existed, the wipers would not have started.This is a truth
dependent on the situation as it was -- there was no ad hoc Metrical
circuit and so on. There are related connections, however, which have
independence of (5) the connection just noted. One is bound
with the fact that we do indeed suppose that there is some set of types of circumstances, each type related in the same way to startings-to-
work of the wipers. We believe that if the wipers did start, even if
certain changes had taken place in the situation there would have
occurred an instance of one or another member of this set of types ot
circumstances. Either the switch was flipped and other conditions
existed or an ad hoc electrical circuit was completed and other
conditions existed, or. ... More generally, suppose again that cc was a
causal circumstance for e. Suppose also that any one of cc or cc' or cc'' or...,
if it existed, would also have been a causal circumstance for e and, we
mig^add, would not have been part of a causal sequence including cc.
Then
(6) If none of cc or cc' or cc" or... existed, even if there occurred any
change x consistent with that and with e's absence, . would still not
have happened. If e happened, at least one of cc or cc or cc or
existed, even if there also occurred any change x consistent with
both.
By way of abbreviation, one or another of a set of possible
circumstances was necessary to e, and e necessitated the occurrence of
one or another of the set.
Our last relation follows on from this. In terms of the example it has
to do with the fact that if in the situation there existed only the one
circumstance for the starting of the wipers, then, even if certain other
events or conditions had occurred or existed, the wipers would not
have started. More generally, if cc was a causal circumstance for e, and
with the other terms defined as with (5), we have this:
(7) If none of cc' or cc" or... existed, then if cc had not existed, even
if any change x had occurred logically consistent with that and with
e's absence, e would not have happened. If none of cc' or cc" or...
existed, then if e happened, cc would still have existed even if any
change x had occurred consistent with e and cc.
By way of abbreviation, for what it is worth, we can say that cc was
dependently necessary to e, that e was such as to dependently
necessitate cc.
Our principal conclusion about causation is now at least in distant
view. Causation and other nomicity consists in no less than, and not
greatly more than, a web of connections between things or events, at
bottom individual properties. What are these connections? They are
. those asserted by the two kinds of conditional statements. Causation
is not, as some suppose, anything less than these connections—which
conclusion will be defended in what follows. Nor is it greatly more.
There is thus a clear and plain answer, if one which requires
complication, to the question of what causation and other nomicity
comes to.
The web may be open to other styles of description. Any of these
must give it as having a certain structure. Each of the connections
stated by independent nomic conditionals gives rise to others. For
example, suppose cc necessitated e, e thus being necessary to cc, and
that cc consisted in c and c'. It follows that if e had not occurred, and c'
had occurred, then c did not occur. We shall not pursue these matters
further here, but they will be noticed again in connection with the
nature of conditional statements and the subject of causation and
science. (1.4, 1.6)
It is worth emphasizing what has already been said or implied, that
all seven of the connections at which we have looked, and the further
subordinate ones at which we shall not look, are indeed objective
connections, connections in reality. They are entirely independent of
minds, theory, conceptual schemes, the statements which state them,
and so on. There are philosophers, some of them inclined to Kant's
doctrine that we impose the category of causation on reality, some of
them freer spirits, who think or at any rate say differently of causation
and of nomic connection generally—in a phrase, that it is part of the
mental order. One of these philosophers presses on forward, with
agreeable audacity, to characterize the view I have expounded as
Idealist or even Scholastic. (Putnam, 1983) That is, the view expoun-
ded is seen as one which 'mentalizes' the natural world by intruding
the mental order—nomic or necessary connection—into it. The view,
on the contrary, is precisely one of Causal Realism rather than Causal
Idealism. (Kim, 1981) It is exactly unlike any theory which does
somehow locate nomic connection in the mental order, whether or not
it then relocates it elsewhere, and thus is properly labelled Idealist.
The point stands in connection with another. Those familiar with
philosophical writing on causation, or touching on causation,, will
have noticed that our analysis so far of it has taken the terms
'necessary connection', 'nomic connection', and 'lawlike connection'
as synonymous, but has made little reference to laws. The analysis
may appear to be unlike those which, to speak quickly and only of one
central matter, describe something like a causal circumstance and an
effect as two items which fall under a law, and then proceed to attempt
to give an account of what a law is—a true proposition of a certain
character. (Hempel and Oppenheim, 1953; Hempel, 1965) These
different analyses may appear to describe a connection in reality by
way of what can be called our linguistic response to it, or the character
of our belief about it. In fact, our analysis and these seemingly different
analyses are basically alike. Both characterize connections in reality
and both give an account of the character of our beliefs about them. It
could not be otherwise.
Our analysis, in a way more direct, specifies necessary connections,
but in so doing does provide an account of the nature of laws. It does so
by actually giving their form or structure. The most fundamental kind
of them are independent nomic conditional statements, general rather
than particular. Laws of the fundamental kind thus are general
propositions to the effect that if something is the case, then no matter
an alteration in certain logically consistent concomitants, something
else is also the case.
The alternative procedure, although its focus is different, is indeed
basically alike, as it must be. Here, one starts with a connection in the
world, and appears to describe it by way of our characterization of it,
the character of our belief about it. To do the latter thing, however, if
the procedure can have any hope of success, is to describe the
connection in the world. If it were not to do this, it would be no more
than the futility of changing or avoiding the subject.
1.4 THE ANALYSIS OF CONDITIONAL STATEMENTS
What we mainly have in answer so far, about causes and causal
circumstances, is that they stand in seven connections—the last three
of which are also fundamental to what will be said of nomic correlates.
All are connections stated by either dependent nomic conditionals or
independent nomic conditionals. What we need now, to have a better
grasp of these connections, is a better grasp of the two kinds of
statements. To understand them more fully is to see more clearly what
we believe about the real connections, connections in extra-linguistic
reality. The subject of dependent nomic conditionals has for long been
a disputed one, and part of larger disputed subjects, those of larger
categories of 'if' statements and of 'if' statements generally.
Dependent conditionals can initially be identified, as they have been
here, as typified by the 'if statements we accept in connection with
our standard causal beliefs—'If the switch hadn't been flipped, the
wipers wouldn't have started', 'Since the switch was flipped, the
wipers started', and the like. The idea, of course is not to elucidate
dependent conditionals by relating them to causal statements and the
like, but to do just the opposite. It will be convenient, by the way, to
abbreviate the conditional 'If the switch was flipped, the wipers
. started' not merely to 'If f occurred, then s occurred', as we have
already, but to 'If F then S'. So too with all other conditionals: letters in
lower case for events, conditions, and the like, the same letters in
upper case for the statements that the event occurred or the condition
existed. The custom will in fact be followed generally hereafter, with
subjects other than that of conditionals.
Dependent nomic conditionals are readily distinguished from a
number of other sorts of 'if' statements. First, they are not logically or
conceptually necessary, as is 'If she has children, she is somebody's
mother.' That they are not such statements is in accord with the fact,
rightly insisted upon by Hume, as already noted, that causes cannot be
said to be in a certain logical connection with their effects: the fact
that it is not contradictory, however mistaken it may be, to assert that
a causal circumstance for an event existed but that the event did not
occur.
Dependent conditionals, secondly, are not to be identified with the
'material conditionals' of truth-functional logic, which rarely if ever
turn up in ordinary language. The 'material conditional' is customarily
written as something like P ] Q. It is only misleadingly expressed as If P
then Q, as is now widely accepted. (Bradley and Swartz, 1983, pp. 226-9;
Anderson and Belnap, 1962) The material conditional P ] Q is true
solely in virtue of P and Q both being true, or both false, or P being
false and Q being true. It is not true in virtue of any further relation
between P and Q. It is false only when P is true and Q false, and false
solely in virtue of those truth-values of its parts. Despite ingenious
if strenuous attempts (Grice, 1975; Ayer, 1972) to present 'if'
statements in general as being material conditionals at bottom, it is
evident enough that our If F then S is not true solely in virtue of the
antecedent and consequent being both true or both false, or false and
true respectively. (Mackie, 1973a)
Thirdly, dependent conditionals are unlike a very considerable and
mixed assortment of 'if statements, (i) 'If she feels so strongly, she'll
decide against it.' (ii) 'If he is reasonable and understands the facts, he'll
send the letter.' (iii) 'If you want them, there are biscuits on the
sideboard.' (iv) 'I could have if I chose to.' (v) 'If I'm awake the sun will
rise and if I'm not awake the sun will rise.' (vi) 'Since you moved your
arm that way, you waved.' (vii) 'The offer was made and accepted, so
there's a contract.' (viii) 'If that was painted in the eighteenth century,
I'm a Dutchman.' (ix) 'If you were Julius Caesar, you wouldn't be alive.'
These are in various ways different, as reflection will show, and raise
different questions. What is common to all of them and to others, as it
is to the first two sorts of 'if statements, is that none states the kind of
connection of one thing with another which is expressed by any
dependent conditional.
This general distinction, clear enough despite our not having an
analytic account of it, is in part brought into sharper focus in a
somewhat unexpected way. There is a difference, although an
uncertain one, between some statements of the form If P then Q and
others of the form If P, Q. (W. A. Davis, 1983a) Suppose that someone
has unkindly disconnected the wiring between the switch and the
wipers. It makes sense to say, and in a certain situation it will be true,
that (1) if the switch is not flipped, the wipers will not start. One can
say quite as truly in this way, of course, that (2) if the switch is flipped,
the wipers will not start. (The case is then like (v) above.) But is it true
that (3) if the switch is not flipped, then the wipers will not start? On
the contrary, it seems false. This is so since this third statement asserts
the existence of a connection between two things (no flipping and no
starting), and ex hypothesi no such connection exists. The first
statement, like the second, can naturally be taken as not asserting such
a connection, and hence can be true. The third statement is a
dependent nomic conditional, while the first, whatever else is to be
said of it, is not. The point is instructive, but it would certainly be
mistaken to suppose that all ordinary conditionals are of the form If P
then Q and all other 'if statements of the form If P, Q.
Dependent nomic conditionals can also be characterized in terms of
their logical properties in a narrow sense. Let us notice two of these.
The seven connections surveyed above (1.2, 1.3) were stated by both a
conditional and its contrapositive. Dependent nomic conditionals, as
can be anticipated, in fact have the logical feature that they do simply
entail their contrapositives. If not-F then not-S entails If S then F, and
the latter entails the former. If F then S entails If not-S then not-F, and
here too the latter entails the former. That there is this mutual
entailment with respect to the two members of each pair is, or is
intimately connected with, the proposition that the two conditionals
state the same fact of connection between two things in the world. The
feature of entailing their contrapositives distinguishes dependent
nomic conditionals from certain other 'if statements. Some of these
are exemplified by (iii) and (iv) above. From 'If you want them, there are
biscuits' it does not follow that if there are none, you don't want any,
and from 'I could have if I chose to' it does not follow that if I didn't
choose to do the thing, I wasn't able to do it.
Dependent nomic conditionals also have the logical feature that
they are transitive. That is, If P then Q and If Q then R, where these are
such conditionals, entail If P then R. It has sometimes been said that
certain other 'if statements are not transitive—for example, 'If J. Edgar
Hoover had been born a Russian, he would have been a Communist', 'If
he had been a Communist, he would have been a traitor', and 'If he had
been bom a Russian, he would have been a traitor'. (Lewis, 1973, p. 33;
Stalnaker, 1975, p. 173) It is said that this proves the failure of
transitivity—the three statements are unexceptionable and the third
does not follow from the first two. There is the objection, however,
whatever else is to be said, that the third statement fails to follow from
the first two only because of an ambiguity—and more precisely
because the consequent of the first conditional is in fact not identical with
the antecedent of the second. We do not actually have in this
supposed counter-example to transitivity what we must have, state-
ments of the forms If P then Q, If Q then R, and If P then R. (Mackie,
1980) Certainly, whatever is to be said of transitivity elsewhere,
dependent nomic conditionals are transitive. They are thus perfectly
suited to the analysis of our beliefs about causal chains or sequences.
Certainly from the facts that r caused s, and s caused t, it follows that r
caused t.
Are dependent conditionals to be characterized more generally in
terms of two categories to which philosophers have given much
attention, those of subjunctive and counterf actual statements? This
seems often to have been assumed. To have a new example, consider
the statement that (A) since it is raining, the balcony is wet. It is an
indicative conditional, a conditional in the indicative mood. Consider
also the statement that (B) if it were raining, the balcony would be wet.
It is subjunctive. Is only one of these, perhaps the second, a dependent
conditional in the sense we have in mind? No, both statements,
although they are different in mood, are such conditionals. (A) is part of
what is stated by stating that rain is making the balcony wet, or
causing the balcony to be wet. (B) is part of what is stated by stating
that rain would make the balcony wet. The distinction between our
dependent conditionals and others is thus not a difference between the
indicative and the subjunctive mood.
It is as clear that another difference between (A) and (B) is no more
relevant. (B) is counterfactual: it implies the falsehood of its ante-
cedent. (A), called by some a factual conditional, implies that its
antecedent is true. The difference is not the distinction between the
class of dependent nomic conditionals and other 'if statements. Both
(A) and (B), to repeat, are dependent conditionals. So is what is
sometimes called an open conditional: If it is raining, the balcony is wet.
It carries no implication as to the truth or falsehood of its antecedent.
Dependent conditionals have often not been distinguished by
philosophers from one or another larger category of 'if statements.
Partly because of this fact, dependent conditionals have been taken as
problematic. The principal problem about them has generally been
said to be that of their meaning or semantics. The problem is to define ,
the meaning of conditionals, to say what it means to say that if
kangaroos had no tails they would topple over, to say exactly what
conditionals mean. (Goodman, 1965, p. 17, p. 23, cf. p. 14; Ayer, 1972,
pp. 120 f., cf. p 118; Lewis, 1973, p. 1; Mackie, 1973, p. 64) As a look at
the philosophy of language and its analyses of 'meaning' or its uses of
'semantics' quickly shows, much more would need to be done to give
us a well-defined problem, but let us not linger. The vague expression
of it is sufficient for our purposes. Let us rather glance at two of what
are presented as solutions to the problem, the metalinguistic and the
possible-worlds proposals. By doing so we shall become clearer about
the problems of nomic conditionals, and hence their solutions. We
shall also avoid a doubt about what will be maintained here.
The metalinguistic proposal (Goodman, 1965), so named because, at
any rate in the first instance, it presents conditionals as being about
other linguistic entities, is along the following lines. What is it to say
that if [R} it is raining, then (W) the balcony is wet? Roughly, it is to say
that the statement [R], and (C) true statements of certain conditions,
and (L) a true lawlike statement, together entail the statement (W).
The proposal, as is allowed by its proposer, faces serious problems,
notably that of explaining the nature of a lawlike statement. It is
nonetheless advanced as being on the right lines.
The possible-worlds proposal can most easily be stated briefly in
terms of a dependent conditional that is counterfactual. To say that it
it were raining the balcony would be wet is to say this: among possible
worlds where it is raining, the one which overall is most like our actual
world is also one in which the balcony is wet. (Lewis, 1973; cf.
Stalnaker, 1975) Or, to interpret the idea in a way less ontologically
extravagant, a way which does not seem to commit us to a plurality of
somehow existing worlds, what the conditional means is this: if our
actual world were different in that it were raining, and differences
overall were in a sense the smallest possible, the balcony would be
wet One source of this theory, to continue in terms of the example, is
the truth that if it were raining, more other things would be different
than that the balcony was wet. For a start, there would be a cause of the
rain and further effects of it—a wet garden and so on. This prevents us
from supposing that the conditional in question, to speak in the
ontologically extravagant way, comes to this: in the possible world
where it is raining, but everything else is the same as in this world save
that the balcony is wet, the balcony is indeed wet.
What we must then do, it is supposed, is to turn our attention to a
primitive idea of over-all similarity between possible worlds. This has
to do both with what are called states of affairs, which we may take
ultimately to be a matter of individual properties, and also what are
called laws. To note a possibility to which we shall return in a
moment, it is allowed that a possible world w' might be more like our
actual world than a possible world w" even though the laws of our
world are to some extent suspended or do not exist in w' and are intact
A bit more will be said of particular features of the metalinguistic
and possible-worlds proposals, but let us first consider something
common to both of them and indeed to other proposals. All of these, to
repeat although there is some uncertainty and inconsistency, are
presented as answers to the question of the meaning or semantics of
certain 'if statements, certainly including dependent nomic con-
ditionals. To think about this even for a moment is to see that
something is amiss.
Does 'If it's raining the balcony is wet' mean, in however large a
tolerable sense, something about other conditions-say the absence of
a canopy over the balcony and so on? As was maintained earlier (1.2),
surely not. The unsatisfactory conclusion that the conditional is about
so much, or rather the unsatisfactory conclusion that the conditional
is about a further statement about so much, follows from the
metalinguistic view. At any rate there follows some such unsatisfac-
tory conclusion pertaining to other conditions somehow described.
Again, does 'If it were raining the balcony would be wet' mean
something about other ways that the world would be different, over
and above the balcony's being wet, if there were the difference that it
was raining? Is the given conditional in part about a cause of rain, or
the wet lawn? It is a remarkable idea, not made better by bravely
labelling the conditional enthymematic. The unsatisfactory con-
clusion, or a related one, follows from the possible-worlds view.
The views are more plausible when taken as answers, or at any rate
materials for answers, to a question quite different from the question
of meaning. They are more plausible when taken as responses to a
question about dependent conditionals which in fact has more claim to
be regarded as the principal one. It can be called the logical problem,
and briefly expressed it is this: in general, what are the premisses or
grounds or bases for dependent conditionals? It is not the question of
what in general we say when we assert such conditionals, or what they
are about, but the question of what reasons we have for saying what
we do. (This is the question that is fundamental with every sort of 'if
statement.) It is our reasons for asserting a dependent conditional
which bring in a good deal more than what is brought in by the
conditional itself. That there was no canopy may be part of why I say
that if it's raining the balcony is wet, but it is not part of what I say.
The metalinguistic view remains in several ways odd and indeed
unsuccessful when regarded in the more plausible way. It may be said
to be on the right lines, but at best it provides materials for an answer
to the logical question, materials which it does not combine properly.
Further, so to speak, one of the materials is indeed inadequate. If we are
seeking an explanation of the grounds of dependent conditionals, and
one of these is given as a lawlike statement, we do indeed require an
explanation of the nature of such a statement. As for the possible-
worlds view, of which a great deal might be said, it too seems to
involve an unanalysed notion of law, although the matter is more
obscure here.
Let us notice only a clear objection for which the way has been
prepared. What we have as premiss for the dependent conditional that
if it were raining the balcony would be wet is roughly this: in that
possible world most like our own in which it is raining, the balcony is
wet. But it is specifically allowed that that world might lack our laws,
including a law which pertains to the rain and the wet balcony. In that
world, to be brief, it could be an accident or mere coincidence that the
rain was accompanied by the balcony's being wet. That could not be
our reason for asserting the given conditional, whatever else is. (Cf. L.
J. Cohen, 1980; Pollock, 1976; Swain, 1978.) Whatever the strengths
and interests of possible-worlds conceptions in several inquiries,
notably formal semantics, we do not here have an acceptable answer to
our question.
On what basis can we assert the dependent nomic conditional that if
(R) it is raining, then (W) the balcony is wet? The short answer is that
we assert it on the basis of two things, an independent nomic
conditional, and (C) a belief about certain conditions, which is a belief
that the antecedent of the independent conditional is in a certain part
true. Again, we assert it since we accept (i) an independent nomic
conditional roughly to the effect that in the world as it is, and within
certain large limits as it might be, if it is raining and certain other
things are the case, then the balcony is wet, and we also accept (ii) that
those other things are the case. It follows that if it is raining then the
balcony is wet.
To be more explicit, it is simplest to take the particular formulation
of the independent conditional just suggested, and anticipated earlier
(1.3), in place of If R and C, even given any X consistent with R and C
and W, then still W. That is, let us have this: Given the world as it is,
or given any changes in it logically consistent with R and C and W,
then if R and C then W. From these two things it follows—as from If
A, then if B then C, and A, it follows that If B then C—that if R and C,
then W. From this in turn, together with C, there follows the
dependent conditional If R then W. To repeat, let us have the
statement (Y) describing the actual events and conditions accompany-
ing r and c in the world as it is, and the disjunctive statement (X) to the
effect that the world is in one way or another otherwise, logically
consistent with R and C, and W. Then our premisses and conclusion
are as follows.
------------------------
If Y or X, then if R and C then W.
Y.
------------------------
If R and C then W.
C.
------------------------
If R then W.
------------------------
This answer to the logical question about dependent nomic con-
ditionals is reassuringly persuasive. Certainly it involves no unex-
plained notion of a lawlike statement. That is not to say that it
involves no notion of a lawlike statement, or, to speak of reality rather
than our language for it, no notion of lawlike connection. It is
unthinkable that any arguable account of dependent conditionals
could be without a notion of lawlike connection, and hence of law or
lawlike statement. As can properly be said, the answer just given to the
logical question rests essentially on an explained notion of lawlike
connection. 'Lawlike connection' is simply another term for what was
earlier (1.3) called fundamental nomic connection or fundamental
necessary connection—and for connections related to it. Fundamental
nomic connection is the connection stated by independent nomic
conditional statements. To rest an answer to the logical question about
dependent nomic conditionals on independent nomic conditionals is
to answer the question in terms of explained or analysed lawlike
connection. The plain answer also has other virtues (Honderich,
1982a), but they need not be sung here.
As for the meaning of dependent conditionals, it is possible and
perhaps necessary to say of them, as it is commonly said of 'if
statements of various kinds, that they are to be taken as primitive, in
the sense of not being open to analytical definition or reductive
analysis. (Certainly one only gets something synonymous, at best, and
no analysis, by rendering 'If P then Q' as 'On the assumption that P is
true, so is Q' or 'In a possible world where P is true, so is Q'.)
Dependent conditionals are thus to be regarded in the way of the
primitive conception or conceptions at the base of any logical system.
That is not to say, however, that their meaning cannot be character-
ized. It has been here, in what has been said already. Their meaning is
such that they are to be distinguished from various other 'if
statements, that they have certain logical properties, and that they are
entailed by independent nomic conditionals together with further
premisses in a way derived from the antecedents of the latter
conditionals.
To turn now to independent nomic conditionals, they can be
identified initially, as they have been, as typified by 'if statements we
accept in connection with our beliefs as to causal circumstances and
effects. They can, as we know, take the form illustrated by this 'if
statement of our current example: If R and C, even if X, then still W.
Their meaning is evidently quite other than that of dependent
conditionals, since they are in part and in a way general. Each such
conditional asserts, with respect to all events or conditions of a certain
class, that the occurrence of any or any set of them, or indeed all of
them, would none the less leave it true that if the conditional's
antecedent is true, so too is its consequent. By antecedent, in terms of
the example, I of course mean only R and C. In virtue of this fact of
generality with respect to independent conditionals they are not tied to
a particular situation, as are dependent conditionals. Their truth is not
dependent on a particular situation. They can be expressed formally in
several ways, making use of the resources and notations of different
logical systems, but are perspicuously expressed in just the forms we
have. We can, as with dependent conditionals, distinguish them from •
other 'if statements, specify their logical properties—including con-
traposition and transitivity—and give their logical relations, notably
their relations to dependent conditionals.
On what is such an independent conditional as If R and C, even if X,
still W based? The answer, in brief, is the method of empirical inquiry,
at its best the method of science. There can be no doubt whatever
about the validity of this method, and no doubt either that its
description has been and remains a matter of controversy, or of several
controversies. One of these, perhaps the most general and fundamen-
tal, has to do with the problem of induction. What is the explanation of
the rational justification we evidently have when we reason in certain
ways from certain premisses to particular or general conclusions about
the world? What is the explanation of why I am right to conclude, as I
am, that if it is raining and certain other things are true, the balcony is
wet—and, in brief, that it would be wet no matter what else were true?
The explanation will include, certainly, past situations both like and
unlike the present one—like, in that they included events and
conditions of the same type as r and c; unlike, in that they included
events and conditions of other types than those accompanying r and c.
The explanation will also include what is related to this and is
absolutely fundamental to scientific method, which is the experimen-
tal procedure of testing and establishing connections by the 'varying of
circumstances', which is essentially the discovery of what is relevant
and what is irrelevant to a given event. (Mill, 1961 (1843), p. 249;
Keynes, 1952, p. 393; Carnap, 1962, p. 230; Honderich, 1991?)
To say this much of the method of empirical inquiry, above all the
method of science, is of course to say little more than nothing.
Anything like an adequate account of the method of empirical inquiry
is out of the question here. One separate point is clear enough,
however. It hardly needs remarking that the experimental procedure of
varying the circumstances fits exactly the account of fundamental
nomic connection which we have. It fits that account better than it fits
others, including a probabilistic account of which a bit more will be
said. (Skyrms, 1980, p. 16) That is a further if subsidiary argument for
the account.
One thing remains to be noticed. It is now clearer than before (1.3)
how fundamental nomic connection, the connection stated by inde-
pendent conditionals, is either the stuff or the basis of all the seven
causal connections. It is the stuff, so to speak, of the last three—(5), (6),
and (7). It is the basis of the first four—(l, la), (2, 2a), (3), and (4). It is
the basis in the sense that each of the dependent conditionals rests on
some independent conditional and a further premiss related to the
antecedent of the independent conditional. Consider the dependent
conditional (3) If c occurred, so did e. Consider also If cc occurred then,
even if there also occurred any change x logically consistent with cc
and e it was also the case that e occurred—which is the first part of
the independent conditional in (5). Circumstance cc, we take it,
consisted in c and also in c', c", ... As with the example
lately considered, it is evident that (3) is entailed by the given
part of (5) together with a statement of the occurrence of
c', c'',...
It would be rash to make the conclusions of this chapter depend
absolutely on exactly the account of certain 'if' statements that has
now been given or intimated. These statements, as already remarked
make up a controverted subject. (Sanford, 1988) It is complete with
competing predilections, schools, logics, methods, and terming
logies—and indeed competing conceptions of the subject, by which I
mean conceptions of just what 'if statements are properly treated
together What I hope to have shown, which is consistent with a
certain tentativeness about what has been said, and with incomplete^
ness is that we do have a grasp of both dependent and independent
conditionals, which grasp can be clarified and which gives to us an
explicit understanding of the seven causal connections that were set
out It is not as if conditionals of the two sorts were near to being
sufficiently problematic or obscure as to make it unprofitable to use
them in elucidation of causes and effects, causal circumstances and
effects, and—to look forward—nomic correlates.
1.5 CAUSAL VERSUS OTHER NOMIC CONNECTIONS
We take causal circumstances and causes to have a nature lacked by
effects This nature presumably explains the truth that if a is a causal
circumstance or cause of b, then b cannot be such of a We ordinarily
say of causal circumstances and causes that they make their effects
happen, but we do not say, and will deny, that effects make either of
the two causal items happen. The philosophical variations on this
usage are many. The causal items are said to be active, to be
productive, to be geneses, to have potency or efficacy. Some philos-
ophical writings on causation consist in good part in a somewhat
numinous insistence on the distinctive nature of the causal items as
against their effects-causes, for example, are declared to be 'powerful
particulars' or 'forceful objects at work'. (Harre and Madden 1975)
We also say of causal circumstances and causes that they explain
their effects, in a sense in which effects do not explain the causal
items. Here, there is less possibility of philosophical variation, but this
second characterization of the nature of the causal items is perhaps as
important as the first. Finally, we take it that effects depend on the
causal items, and that the latter do not in this way depend on the
former. It is perhaps a good deal less than certain that this third
characterization is conceptually distinct from the first two. I shall
suppose it comes to much the same.
In our inquiry into causation so far, we have not attended
specifically to this fact of difference or asymmetry between causal
items and their effects—the fact of causal priority as it is sometimes
called. We do indeed have it that a causal circumstance necessitated
its effect. But to assert that is by definition to assert no more than a
certain independent conditional—roughly, that since the circum-
stance existed, even if most other things had been different, the effect
would still have occurred. We also have it that effects do no more than
dependently necessitate their causal circumstances. That is to say,
roughly, that if the effect occurred, and no other causal circumstance
for it but one existed, that one would still have existed even if most
other things had been different. It is not obvious, although it may be
true, that the ideas that a causal circumstance made its effect happen,
and explained it, and that the effect depended on the circumstance,
somehow come to no more than these independent conditional claims.
Philosophers have sometimes denied that the asymmetry between
causal items and their effects is a matter of connections stated by 'if
statements. These, they feel, are not enough.
Certainly we cannot rest with the three ordinary ideas we have of
the distinction between the causal items and their effects. The first
idea is of a metaphorical and anthropomorphic kind, and the second
and third also call out for analysis, if only for the reason that there are
other non-causal pairs of things such that the first explains the second
and the second depends on the first. The obvious example is that of the
premiss and conclusion of a deductive argument. It is not that kind of
explanation and dependence that is in question with causation. What
kind it is needs to be explained.
If we cannot rest with the ordinary ideas, we can no more rest with
their philosophical variants. It is all very well to insist that causes have
or are powers or whatever, but we need to know what is to be
understood by that. They do not give commands and they are not
premisses from which many or important conclusions follow. Nor
does it seem likely that the idea of causal power is not open to analysis,
or, what comes to much the same, that it is somehow to be acquired
without noticeable effort by thinking on what is common to such
verbs as 'push' and 'pull', as has sometimes been supposed.
One persistent analytical account of causal priority does seize upon
an indubitable truth, that causal items stand to their effects as our
means to our ends, while no effect is our means to its cause or causal
circumstance. When it is true that an effect—the wine bottle's being
open—is my means, it is not such as an effect but as a cause of
something else, which other thing is not a means to it. We do indeed
manipulate and control our surroundings, in so far as we can, by way of
things as causal rather than as effects. However, there is the immediate
objection that not all causal items are the means of someone. No
earthquake is, and in fact relatively few causal items in the natural
world are such. The attempt has been made, inevitably, to extend the
idea of a means to cover all causal items, (von Wright, 1971; Mellor,
1986) This stratagem is not reassuring, for several reasons, but there is
a more fundamental objection which applies even to those causal
items which really are our means.
It is that the fact that a causal item is a means is not a fact about it,
but a fact about us. The fact that a cause of the wine's being cool, say
refrigeration, is my means—this is the fact that (i) I can bring about
that cause, and (ii) it is a cause of what I desire. This thought, that the
given cause of the wine's being cool is not in or of itself a means, is
reinforced by the truth, among others, that the given cause is precisely
not a means to my idiosyncratic drinking companion, who likes his
Haut Poitou uncooled. But the asymmetry of causal items and their
effects is, of their very nature, a fact about them, a fact which would
persist in a world devoid of desires, and, as might be added, a world
devoid of our capability of bringing things about.
Is it possible to explain the asymmetry by way of a clear idea of
power—or capacity, ability, or disposition? Well, we can give a certain
clear sense to saying that the hot coffee is able or has a power to
dissolve the cube of sugar. What it is in general for a thing a to have the
power to produce b is for it to be true that an individual property or
properties of a, together with other things, will constitute a causal
circumstance for b. Anything that is a cause, then, is in this clear sense
a power, a power to produce an effect. (Cf. Ayers, 1968.) There is a
related secondary sense of the term 'power' and like terms, where the
power is the class of differing individual properties or property-sets,
each of which is nevertheless alike in entering into some causal
circumstance for one effect. Or, better, a power of this kind is the class
of types of such properties or property-sets. In this sense, hot coffee can
be said to share a power to dissolve sugar with steam, certain
chemicals, and so on. The secondary sense is clearly dependent on the
primary.
We need to reflect, however, on what has just been said: in brief, that
for something to be or to have a power in the primary sense is for it to
enter into a possible causal circumstance. Given our account of causal
circumstances, that is fundamentally to say, in line with the
independent conditional (5) set out in Section 1.3 and mentioned at the
beginning of this section, that for a to have the power to produce b is
for roughly this to be true: If A & C, even if X, still B—where C asserts
the existence of other conditions or events. The difficulty is that a like
conditional (derived from the independent conditional (6) also set out
in 1.3) may well be true of b. That is, it will be true, if there is no other
causal circumstance for b on hand, and no alternative for a, that If B &
C, even if X, still A. To speak informally, in terms of the example, the
hot coffee together with other things guaranteed dissolved sugar, but it
may also be true that the dissolved sugar, together with (different)
other things, guaranteed the hot coffee. The upshot of this is that in
this sense of 'power'—as of many like terms—it is at least arguable not
only that a cause has a power to produce its effect, but also that an
effect has a power to produce its cause. Here we have no adequate
difference between cause and effect. It is true, somehow, that a cause
has a power in a sense that an effect does not, but we have not got that
sense.
There is the further grave difficulty about the idea in hand, as a little
reflection will show, that in the given sense no causal circumstance,
as distinct from cause, has the given power. Leaving aside several other
good attempts to explain the difference between causes and causal
circumstances and their effects, and also what can be said of great
obstacles in the way of these attempts (Mackie, 1974, Ch. 7, 1979;
Ayer, 1984a; Sanford, 1976, 1985; Papineau, 1985b; Honderich, 1986),
let us return to and concentrate on our ordinary convictions about the
difference.
What do we have in mind in taking it that a causal circumstance
makes an effect happen? A good answer is that we regard the causal
circumstance as leaving no room for any other eventuality than the
effect. The causal circumstance settles that but one of certain
possibilities becomes actual. Most plainly, the causal circumstance
fixes or secures the occurrence of just one thing, as distinct from fixing
the occurrence of that thing or a second or a third or. ... What do we
have in mind in taking a causal circumstance to explain an effect in
the given sense? There are the same good answers. It is for the
circumstance to leave room but for one eventuality, for it to settle
things. It is not for the circumstance to give rise to something or other,
but for it to give rise to just the effect.
These several glosses of the characterization of a causal circum-
stance as making its effect happen and explaining it, glosses which are
surely very natural, lead us to a firm conclusion, one that may be
anticipated. If it is not obvious, as remarked before, it surely is true
that the nature of causal circumstances and causes, as against effects,
is, at least in good part, explained by what we have already—it is
explained in good part by the fact that causal circumstances necessi-
tate effects, and effects merely necessitate one causal circumstance or
another. That is, to simplify the independent conditional (5) a bit, a
causal circumstance is such that if it happens, then just its effect does.
But, to simplify (6), an effect is such that if it happens, then all that is
true is that one or another of a set of causal circumstances has existed.
The clear distinction made by these two conditionals gives a clear
sense to talk, mainly by philosophers, of causal circumstances having a
power lacked by effects, and so on. To revert to what is fundamental,
the distinction made by the two conditionals gives some clear sense to
our saying that causal circumstances explain effects, and make them
happen, and not the other way on. More needs to be said about our
conviction, but here we have something. We have in a causal
circumstance by itself a complete answer to the question of why an
effect occurred. We do not have, in just an effect, such an answer to the
question of why a causal circumstance occurred. That we do not have
such an answer, it can be argued, is the fact that what follows, from the
occurrence of the effect, is only that that circumstance or another
occurred.
I have latterly been speaking only of causal circumstances, and not
causes. What has been said can be extended to them. That is, in brief, it
is reasonable to suppose that their nature, as distinct from that of
effects, is to be explained by their membership of causal circum-
stances. What has been said, however, seems not enough. It is, I think,
one of two parts of an adequate account of causal asymmetry. The
additional part, which does not have to do with the connections stated
by independent conditionals, is perhaps particularly necessary in
connection with our conviction about the explanatoriness of the
causal items.
Both that conviction, and the conviction that the causal items make
their effects happen, can also be glossed as convictions that the causal
items bring into existence their effects. Given this, it is impossible to
avoid the idea that another part of the difference between the causal
items and their effects is that the causal items exist at a time when
their effects do not. They exist before their effects. If all causal
circumstances and causes precede their effects in time, it seems we
have in that temporal consideration a second basis for the asymmetry
we are considering. Do all of what we take to be causal circumstances
and causes precede their effects? Here there is a large philosophical
dispute, and we shall be told by some that the answer is no. Is there not
a causal circumstance, including the weight of the driver, for that
simultaneous effect which is the flattening of the seat cushion?
One thing that can be said in opposition to the simultaneity idea is
that if we persist in thinking precisely of causation, of one thing
causing another, as distinct from any related kind of connection, we
are inclined to try to substitute successions for simultaneities. We are
inclined to think of connections between earlier and later events rather
than connections between simultaneous events. The flattening of the
seat cushion at this instant is owed to the driver's weight at a prior
instant. The last instant of the flattening of the cushion, we are
inclined to think, will be simultaneous with the beginning of a causal
circumstance for the cushion's being other than flattened. In this
inclination to take the causal items as prior to their effects, incident-
ally, we have the support of a good deal of science, indeed a strong
scientific tradition, having to do with the principle of retarded action.
(Bunge, 1959, p. 62f.)
In our ordinary thinking about causation and time there evidently is
uncertainty, as is not the case elsewhere. In some respects there seems
not much room for argument about our conception of standard effects
and their causal circumstances. There is surely no doubt that we take
them to involve the necessity relations and the relations of required-
ness. In connection with time, our conception is not settled. This fact
is consonant, to say the least, with the long philosophical dispute
about causation and time, including the idea that causes might not
only be simultaneous with their effects but might come after their
effects. (Dummett, 1954) If we are subject to uncertainty, there is room
for decision, as distinct from discovery. The definition we shall adopt
here, in the tradition of Hume and many others, is one that takes
causal circumstances and hence causes to precede their effects in time.
It allows us the conclusion that has just been contemplated: that the
difference between causal items and their effects has its basis not only
in the consideration that causal circumstances fix uniquely the
occurrence of their effects, but also in the consideration that causal
circumstances precede their effects. The definition is adopted, of
course, not merely for the reason that it gives us a further explanation
of the difference between causal items and their effects. It has an
independent recommendation, although one that needs more argu-
ment that has been supplied here.
Given the account we have of the difference, we can now proceed
quickly to a final characterization of a causal circumstance. We have
everything in hand save one consideration, having to do with non-
redundancy. The difference between causal circumstances and their
effects, further, is what distinguishes causal circumstances and effects
from other things also in nomic connection, which is to say nomic
correlates. We can also proceed quickly to a characterization of these.
We began with the idea that a causal circumstance consists in a set
of conditions including a cause or causes—more precisely a set of
individual properties—each being (1, la) required or alternatively
required for the effect. From this it followed (2, 2a) that the
circumstance too is required or alternatively required for the effect.
Further (3) each condition requires the occurrence of the effect, and so
too (4) does the circumstance as a whole. As for the fundamental
necessity-relations, (5) the causal circumstance necessitates the effect,
and hence the effect is necessary to the circumstance. (6) Also, the
circumstance is one of a set of circumstances necessary to the effect.
Further (7) the causal circumstance is dependently necessary to the
effect, which is to say that the effect dependently necessitates the
circumstance. We have it too (8) that the circumstance (whose
constituents need not be simultaneous) is prior in time to the effect. It
is in virtue of (5), (7), and (8) that we can truly say that the
circumstance makes happen and explains the effect, and not the other
way on.
The property of a circumstance that (5) it necessitates its effect,
although we did not pause to consider the matter, is in a way essential
to a final element in a definition of a causal circumstance, more
particularly a specification of what is included in such a circumstance.
To return again to the beginning, a circumstance (1) consists of items
required for the effect. That is not to say that a circumstance includes
all such conditions of the effect. Which ones then? The answer is that
(9) a causal circumstance is to be taken to include no more conditions
than are needed to necessitate an effect. That is, it includes just a set
of conditions such that if the set existed, so did the effect, and still
would have even if certain other conditions or events had also existed.
Nothing is redundant. To take a causal circumstance as having no
redundancy is obviously to exclude things wholly irrelevant to the
effect. With respect to the circumstance for the starting-to-work of the
windscreen wipers, the car's radio being on is likely to be irrelevant.
Other things are not irrelevant in the given sense, since they are
required conditions of the effect—but they are not part of the causal
circumstance. A causal circumstance, in accordance with the non-
redundancy criterion, does not include a particular condition and also a
causal circumstance for that condition, or any part of one. In specifying
a circumstance for the working of the wipers, we may include the
switch's being flipped, but if we do, we cannot also include the muscle
movements which gave rise to the switch's being flipped. Certainly we .
do not need to try to go into the whole causal history of an event in
order to specify something—one of the many sets of things—that had
the property of making the occurrence of the event necessary. In
general, if c is in a causal circumstance cc, and c is the effect of cc',
then cc' cannot be part of cc and neither can any part of cc'. Equally, a
causal circumstance cc for an event e does not include any other effect
than e, perhaps an effect in a causal sequence connecting cc with e. To
speak loosely, a causal circumstance does not include two or more
links of any one causal line running through it from past to future.
We shall have no need of a fuller definition of a causal circumstance
than the informal one we now have—given in the nine propositions
above. What will be of greater value is a partial characterization which
mentions only those features (9, 5, 8, 7, in order of appearance in the
partial characterization) which will be of most importance in what
follows immediately. Thus, if cc was the only causal circumstance for
an event e, then
cc was no more than a set of conditions or events which necessitated
e, and preceded e, and was dependently necessitated by e.
As already noted, and as will be of some importance later in this
inquiry, the temporal feature does not require that the constituents of
the causal circumstance be simultaneous. The point will be of
particular relevance in connection with causal sequences or causal
chains, to be considered later in the most relevant context. (3.1)
What is bound to come to mind at this point is that there are pairs of
things distinct from, but fundamentally like, a causal circumstance
and its effect. Certainly the thought must occur to anyone acquainted
with almost any part of science, or even a small selection of scientific
laws. Such pairs of things enter into what is variously described as
interaction, reciprocal causation, functional interdependence, func-
tional relation, concomitant variation, and so on. Such pairs of things
are like a causal circumstance and its effect in that they stand in
fundamental nomic or necessary connection (1.3), which is to say some
connection stated by an independent nomic conditional statement.
They differ from causal circumstance and effect in that they lack either
or both of the features that give rise to the difference between causal
circumstance and effect—the priority of the causal circumstance.
Thus (i) neither may precede the other, or (ii) they are not such that one
necessitates the other while the other merely dependently necessitates
it, or (iii) they may lack both features. What is true, rather, is (i) that
they are simultaneous, or (ii) each necessitates the other, or (iii) they
are simultaneous and each necessitates the other. Such pairs are by
definition nomic correlates.
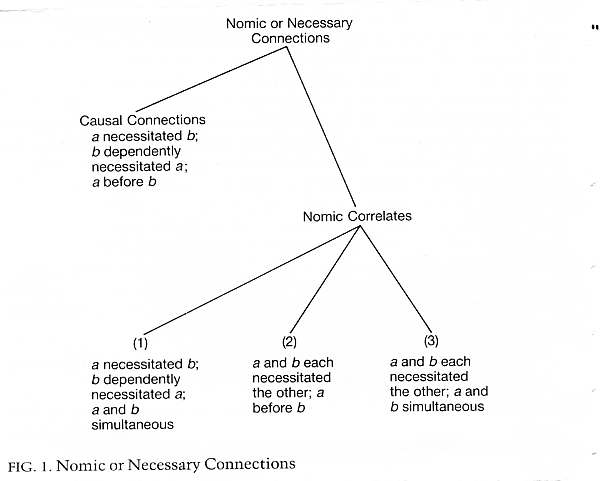
As in Figure 1, then, we have four principal categories of nomic or
necessary connection, each involving some fundamental nomic con-
nection but differing in some respect from each other category. Each of
the three categories of nomic correlates is open to further description,
as will be anticipated. For example, with respect to the first category of
nomic correlates, the category which will be of most importance to us,
there is the truth that if a necessitates b, then b is necessary to a. Also,
if b dependently necessitated a, then a was dependently necessary to b.
Certain objections to these conceptions, objections having to do
with science, will be considered later. Let me say now only that there
is no established conception or usage for 'nomic correlate' or other
more or less equivalent terms used in talk of interaction, functional
interdependence, concomitant variation, and so on. No doubt, with
respect to the first and second categories of nomic correlates, it is
possible to call the second member an effect without seeming to
misuse language, including this or that scientific language. It is also
possible, also without such misuse, not to call the second member an
effect, but to call it a nomic correlate instead, as we have. It is on the
way to being as reasonable as refusing to say about the see-saw that one
end's going down is the effect of the other end's going up. It is
reassuring to be able to say that the inquiry to come does not depend
on our decision. We shall be concerned with the first category of nomic
correlates, and refer to them as nomic correlates, but it is their nature
rather than their name that is important.
It will be noticed that in all of this the term 'correlate' is being used
in a way consistent with our previous uses of 'event', 'cause',
'condition', 'causal circumstance', and 'effect': not for a type of thing,
but for a thing itself, more particularly an individual property or set of
such properties rather than a type. To use the term 'event' for a token
rather than a type is ordinary. So with 'cause' and 'effect'. 'Condition'
and 'causal circumstance' can also be used in this way. The ordinary
use of the term 'correlate', where it is ordinarily used, is perhaps for a
type of individual rather than an individual. We are departing from this
usage, and must put up with some inconvenience, in order to have
consistency and hence clarity in several contexts. Nothing substantial
hangs on the decision.
One last and related point. We have found causation to consist, at
bottom, in connections between particulars. We have analysed the
particular statements which state these connections. Some of these,
analysed by way of independent nomic conditionals, are in a way
general. (1.4) They are distinct, however, from causal generalizations,
which will be of some importance in what follows. Much might be said
of the relation between particular and general causal statements, but
here a little must suffice. If we maintain that cc was a causal
circumstance for e, we are maintaining the conditionals of which we
know, notably that if cc occurred, then even if certain things of a general
class had also occurred, e would still have occurred. This is evidently
in a way general. By asserting it, however, we are also committing
ourselves to a general conditional proposition of a standard kind. We
cannot make the causal claim about cc and allow that other
circumstances identical with cc have different upshots. If we take the
starting of the wipers to be an effect of a given circumstance, we must
accept that there is a type of circumstance which is connected with
starlings of wipers generally. What is true, to express the matter
simply, if cc was a causal circumstance for e, is this:
If any circumstance of the type of cc occurs, even if certain other
events or conditions also occur, so does an event of the type of e. If
the event does not occur, neither does the circumstance.
We are committed to other such generalizations, less simple, one of
them related to the fact that a circumstance is dependently-necessary
to the occurrence of an effect. We are similarly committed in
connection with nomic correlates.
Editor's Footnote
This selection is from the first chapter of Honderich, A Theory of Determinism: The Mind, Neuroscience, and Life-Hopes (Oxford University Press). The selection also appears in Mind and Brain (OUP), the paper which reprints the first half of the longer book. The remainder of the chapter considers objections and alternative views. For a very much simplified account fundamental causal connection, see How Free Are You? The Determinism Question (OUP, 1st & 2nd editions).
HOME to Det & Free Website front page
HOME to T.H. Website front page