


Next: Calculation of the force
Up: Theoretical overview
Previous: Theoretical overview
Phonon frequencies
The central quantity in the calculation of the phonon frequencies is
the force-constant matrix
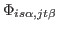 , since the
frequencies at wavevector
, since the
frequencies at wavevector 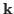 are the eigenvalues of the
dynamical matrix
are the eigenvalues of the
dynamical matrix
 , defined as:
, defined as:
![\begin{displaymath}
D_{s \alpha , t \beta} ( {\bf k} ) = \frac{1}{\sqrt{M_s M_t}...
...R}_j^0 + {\bf\tau}_t - {\bf R}_i^0 - {\bf\tau}_s) \right] \; .
\end{displaymath}](img6.png) |
(1) |
where 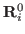 is a vector of the lattice connecting different
primitive cells and
is a vector of the lattice connecting different
primitive cells and 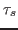 is the position of the atom
is the position of the atom 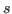 in
the primitive cell. If we have the complete force-constant matrix,
then
in
the primitive cell. If we have the complete force-constant matrix,
then
 and hence the frequencies
and hence the frequencies
 can be obtained at any
can be obtained at any 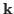 , so that
, so that 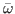 can be computed to any required precision. In principle, the elements
of
can be computed to any required precision. In principle, the elements
of
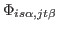 are non-zero for arbitrarily large
separations
are non-zero for arbitrarily large
separations
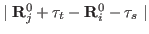 , but in practice they decay rapidly with separation,
so that a key issue in achieving our target precision is the cut-off
distance beyond which the elements can be neglected.
, but in practice they decay rapidly with separation,
so that a key issue in achieving our target precision is the cut-off
distance beyond which the elements can be neglected.
Dario Alfe`
2012-02-20
![]() , since the
frequencies at wavevector
, since the
frequencies at wavevector ![]() are the eigenvalues of the
dynamical matrix
are the eigenvalues of the
dynamical matrix
![]() , defined as:
, defined as: