The program also calculates the density of states, writing the file
DOS. The input variables:
DOSIN = 0; DOSEND = 25; DOSSTEP = 0.1; DOSSMEAR = 0.02
specify the starting and the ending frequency (in THz), the step and the smear. The smear is the width of the Gaussian which is convoluted with the dos spectrum. The density of states will be calculated using the available frequencies, which in this case are those coming from the dispersion curves. This is not the best way to do, because the DOS is the integral over the whole BZ of the phonon frequencies, and the dispersions along some special directions do not usually provide a good sampling of the BZ.
The correct way to calculate the density of states is to generate a
set of points which accurately sample the BZ, and calculate the
frequencies at these points. This can be done with the following
settings:
LFREE = .TRUE.; TEMPERATURE = 1000
LGAMMA = .FALSE.
QA = 11; QB = 11; QC = 11
QA, QB and QC are the divisions for a Monkhorst and Pack (MP)
[3] special points grid generations, LGAMMA =
.TRUE. means that the grid will pass through 
. With the
setting LFREE = .TRUE. the program will also calculate zero-point
energy, Helmholtz free energy, internal energy, specific heat and
entropy, at the temperature given by the variable TEMPERATURE in
degrees Kelvin. The MP special points are written in the file QPOINTS,
which can be used for subsequent calculations without generating the
points again (dense meshes can take time to be generated) by setting
QA to a negative number (default).
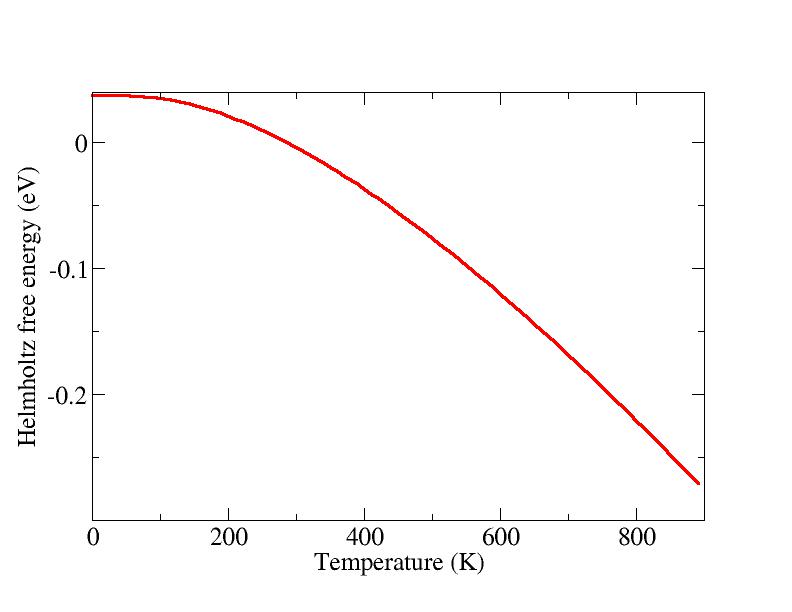
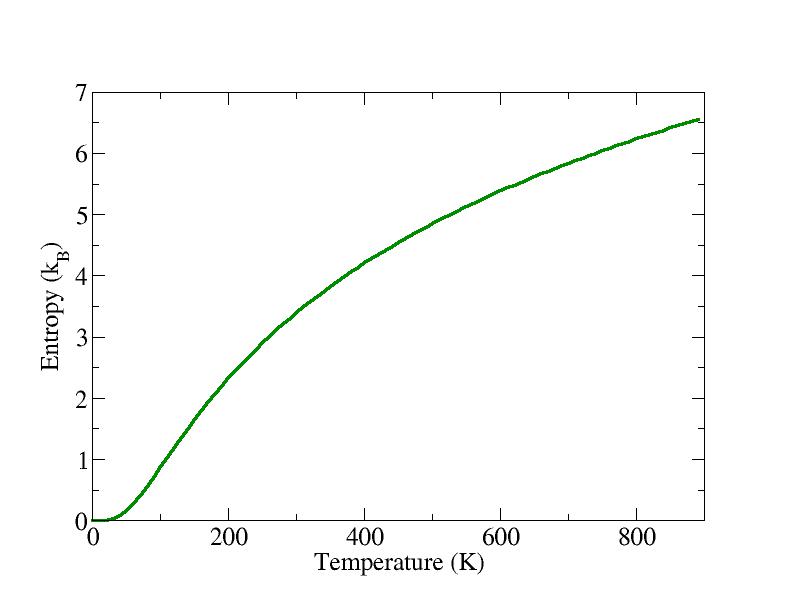
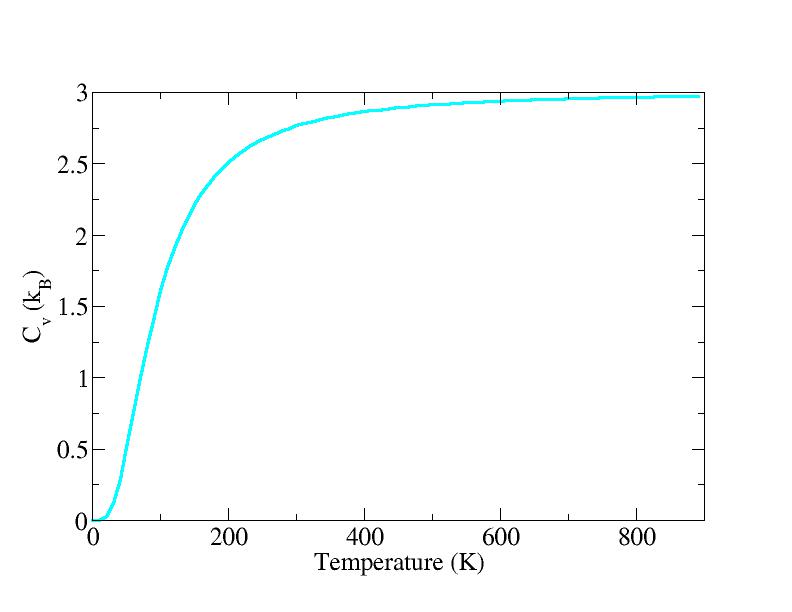
A convenient way to generate a set of thermodynamic properties as
function of temperature is to set the variable:
PTEMP= 10 90
This will create a file called THERMO, which contains the internal
energy, the free energy, the free energy in the classical limit, the
entropy and the constant volume specific heat, as function of
temperature, in the example above starting from a temperature equal to
the value of the input variable TEMPERATURE, in steps of 10 K, for 90
steps.
