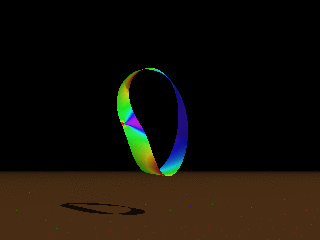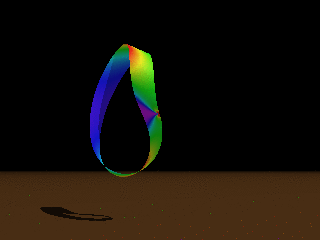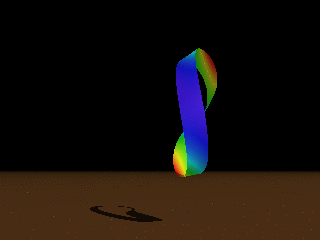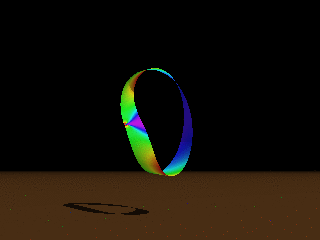The equilibrium
shape
of an elastic
developable Möbius strip
|
|
|
|
|
Figure: Computed Möbius strips of aspect ratios 5π,
2π, π, 2π/3.
|
|
Colour codes the bending
energy density (from violet for almost flat regions to red for highly bent).
|
The Möbius strip obtained by taking a rectangular strip of
plastic or paper,
twisting one end through 180
degree, and then joining the ends,
is the canonical example of a
one-sided surface.
As
simple experimentation shows, a physical Möbius strip, when left to itself,
adopts
a characteristic shape independent of the type of material (sufficiently stiff
for gravity to be ignorable).
This
shape is well described by a developable surface that minimises the deformation
energy, which is entirely due to bending.
We assume that the material obeys
Hooke's linear law for bending,
then the energy is proportional
to the integral of the non-zero principal curvature squared over the surface of
the strip,
which is taken to be an isometric
embedding of a rectangle into 3D space.
The
problem of finding the equilibrium shape of a narrow Möbius strip was first formulated in 1930 by M.Sadowsky who
turned it into a 1D variational problem represented in a form that is invariant
under Euclidean motions.
Later
W.Wunderlich generalised this formulation to a strip of finite width,
but the problem has remained open although
geometrical constructions of developable Möbius strips have appeared.
We apply an invariant geometrical approach based on the variational bicomplex
formalism to derive the first equilibrium equations for a finite-width
developable strip thereby giving the first non-trivial demonstration of the
potential of this approach. The boundary-value problem for the Möbius strip offers a fitting example for application of
these equations.
Numerical
solutions for increasing width-to-length
ratio show the formation of creases bounding nearly flat triangular
regions,
a
feature also familiar from fabric draping and paper crumpling.
This
suggests that our approach could give new insight into energy localisation
phenomena in unstretchable elastic sheets,
which
for instance could help to predict points of onset of tearing.
Reference:
E. L. Starostin &
G. H. M. van der Heijden. The shape of a Möbius strip.
Nature Materials 6 563-567 (2007) Published online
15July 2007. DOI:10.1038/nmat1929
|
|
|
|
|
|
|
|
|
Figure: Computed Möbius strip of aspect ratio 5π.
|
|
Colour shows the bending energy
density (from violet for almost flat regions to red for highly bent).
|
About:
· J.H. Maddocks. Mathematics: Around
the Möbius band. Nature Materials 6
547-548 (2007) Published online 15July 2007. DOI: 10.1038/nmat1960
· Möbius strip
unravelled. News@Nature.com Published online 15 July 2007. DOI: 10.1038/news070709-16
· Research Highlights: Möbius in
equilibrium. Nature Physics 3 513 (2007)
DOI: 10.1038/nphys694
· A New Twist on the Möbius Strip. ScienceNow Daily News 16 July 2007
· A Twist on the Möbius Band. Science News, week of July 28, 2007; Vol. 172, No. 4
· Maths of Möbius strip finally solved. New Scientist, issue 2613, 21 July 2007, p. 6
· Shaping Up a Möbius Strip. Scientific American.com July 17, 2007
· Rätsel des Möbiusbands gelöst. Spiegel.de 19. Juli 2007
· Moebius strip riddle solved at last. Cosmos
16 July 2007
· Rätsel der Endlos-Rennstrecke gelüftet. Sueddeutsche Zeitung 24.07.2007
· A Twist on the Möbius Band. Math in the Media, August 2007
· Articles about modeling the shape of a Möbius strip. Math Digest, July 2007
· Möbius at rest. +Plus Magazine 03.08.2007
· Möbius Problem Solved. Nanoarchitecture.net 16 July 2007
· Scoperto il segreto del
· Le equazioni del
· La forme du ruban de Möbius n’a plus de secret. Science &
Vie No. 1080 Septembre 2007, p. 14
· Comment se forme un ruban de Möbius ? La Recherche No. 412 Octobre 2007, p. 28
· Research Highlights 2007: Mind over Möbius.
Nature 450, p. 1132,
20 Dec 2007
See also:
L.Frazier, D.Schattschneider. Möbius
bands of wood and alabaster. Journal
of Mathematics and the Arts 2(3) 107-122 (2008). DOI: 10.1080/17513470802222926
H.Dambeck. Rätsel des Möbiusbands gelöst. In: Numerator. Mathematik für jeden, S. 132-136. ISBN:
344215572X
|
|
|
|
|
|
|
|
|
Figure: Computed Möbius strip of aspect ratios 5π,
2π, π, 2π/3.
|
|
Colour shows the bending
energy density (from violet for almost flat regions to red for highly bent).
|