PHAS0061 Advanced Topics in Statistical Mechanics (formerly PHASM/G228)
UCL moodle site
The
purpose of this module is to demonstrate that we have mathematical
tools and physical intuition with which to describe complicated
time-dependent systems. In many treatments, the scope of statistical
physics is limited to equilibrium systems, but this is only half the
story. We shall start with equilibrium, but the prime objective is to
discuss nonequilibrium phenomena such as cooling, diffusion and
fluctuation-driven barrier crossing phenomena such as first order phase
transitions. We give particular attention to foundational issues in
statistical physics, such as the paradox of irreversibility emerging
out of reversible mechanics, and of course the process of entropy
production and the second law of thermodynamics.

- To develop understanding of statistical physics beyond an introductory module.
- To use statistical mechanics to deduce the
properties of systems of interacting particles, with emphasis on the
liquid state, interfaces and small clusters, and to discuss the
nucleation of phase transitions.
- To introduce the mathematics of stochastic processes, including the Langevin equation and Fokker-Planck equation.
- To understand how stochastic dynamics may be derived from deterministic dynamics.
- To introduce the techniques of stochastic
calculus, noting the distinct Ito and Stratonovich rules, and to apply
them to solve various problems, such as Brownian motion, including
their use in areas outside science such as finance.
- To consider the meaning of entropy and its
production in statistical physics, with reference to the reversibility
paradox and Maxwell’s demon.
- To develop the concepts of work, heat transfer
and entropy production within a framework of stochastic thermodynamics,
and to derive fluctuation relations.
Syllabus
Part 1 Systems of interacting particles
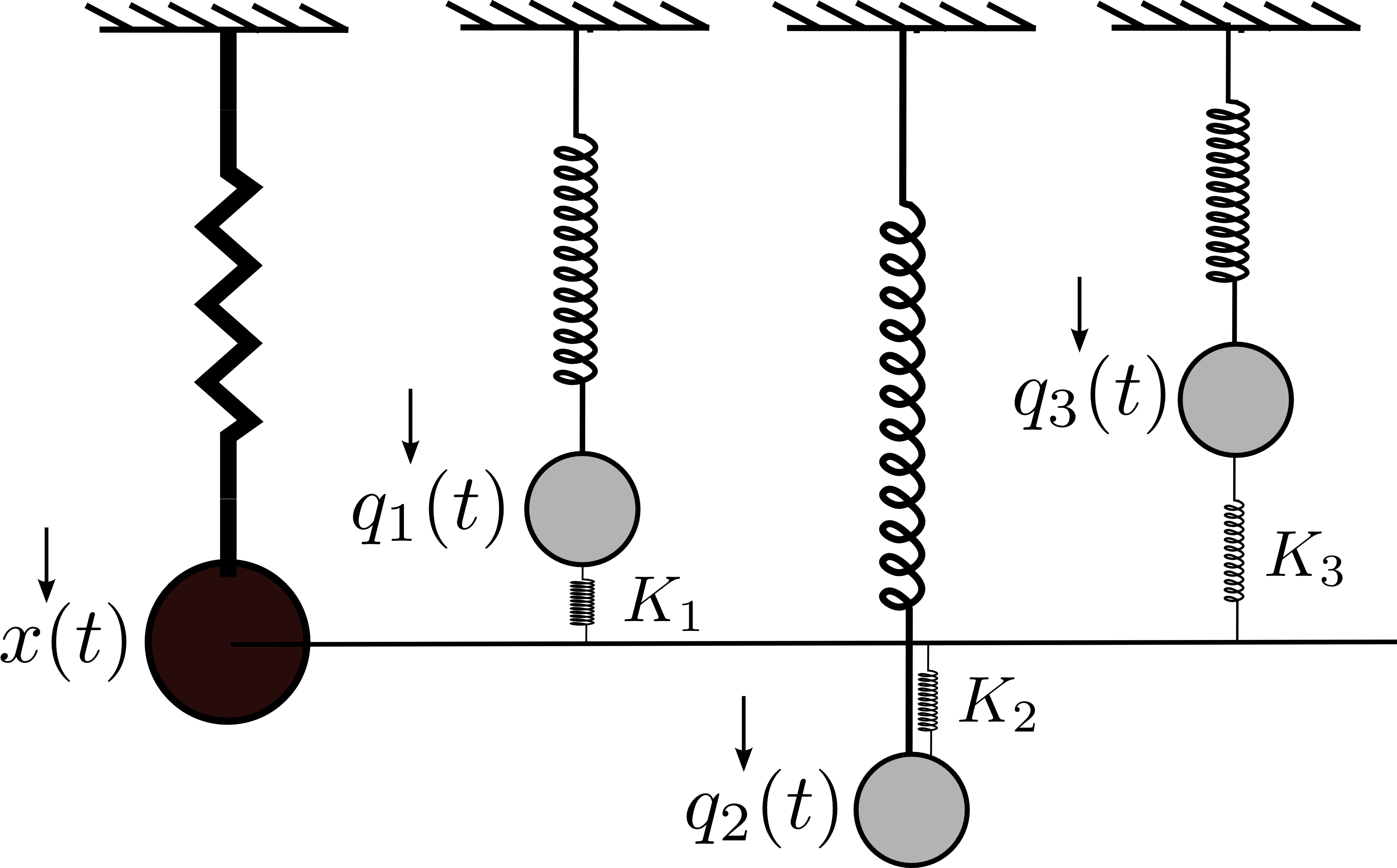
Partition functions of harmonic structures
Virial expansions
Thermodynamics of phase coexistence
Potential of mean force
Monte Carlo and Molecular Dynamics simulation
techniques
Many-particle phase space dynamics.
Liouville’s theorem and the H-theorem
Part 2 Stochastic processes
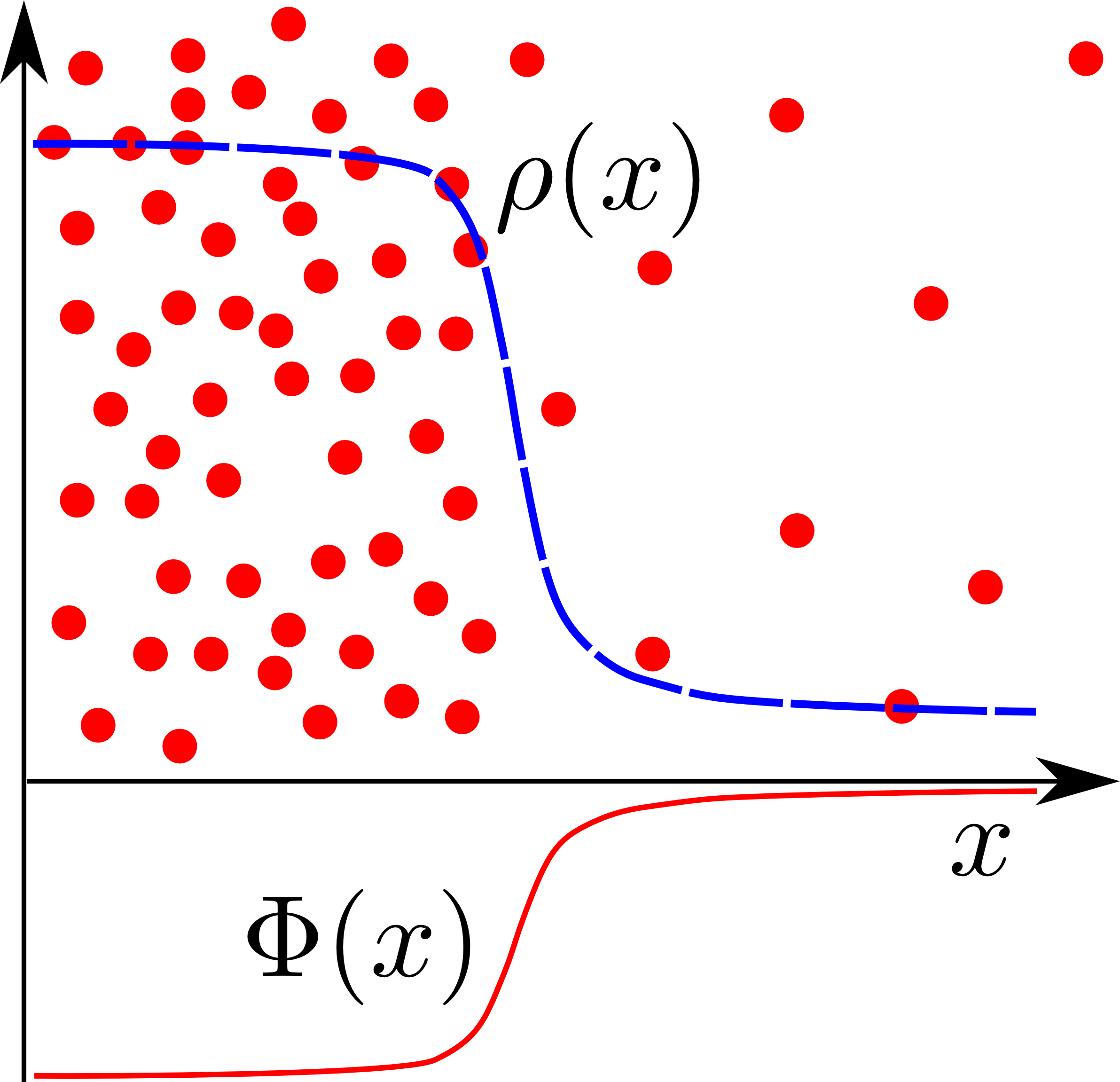
Fluctuations, uncertainty and entropy
Random walks and Brownian motion
Master equations of macrostate probability
dynamics
Nucleation and aggregation kinetics
Fokker-Planck equation
Langevin equation, fluctuation-dissipation
relation
Green-Kubo relations
Stochastic differential equations and Ito’s lemma
Ito-Stratonovich
dilemma
Financial modelling
Part 3 Irreversibility
Philosophical issues
Entropy production and Loschmidt’s
reversibility paradox
Coarse graining and projection of dynamics
onto smaller phase spaces
Caldeira-Leggett model
Stochastic thermodynamics and fluctuation
relations
Maxwell's Demon
Table of contents