Modelling of spatio-dynamical systems
Complex spatial nonlinear dynamical models offer a wide range of stimulating statistical challenges with interesting and important potential implementations. The motivating application of our novel methodology lies in cell motility. The motion of migrating cells takes many different forms and is affected by a variety of factors; take, for example, the motion of immune cells within the lymphnode, or the migration of dictyostelium cells towards chemokinetically rich regions. Advances in 2p microscopy (see Figure 1 below) allow us to trace the motion of immune cells within the lymphnode of a live mouse.
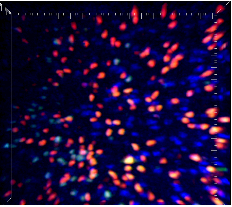
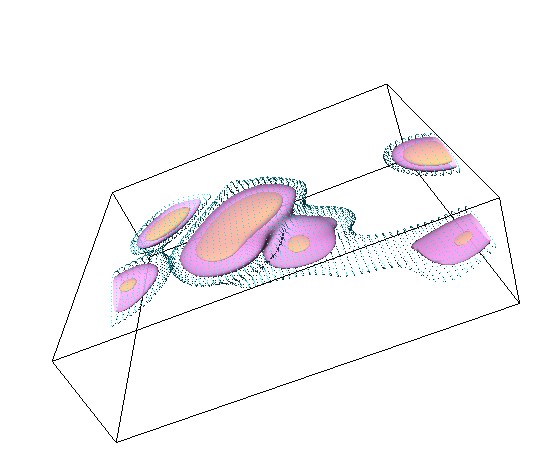
Efficient immune cell migration is of paramount importance in immune defense, so understanding and characterizing cellular motion is key. We introduce a statistical model for inferring the chemokine fields that guide lymphocyte migration. We assume that cells are well-descibed by a Langevin diffusion process with a force field. Under suitable model assumptions on the underlying force field, and owing to the Markovian structure of the Langevin process, the cell trajectories follow a Gaussian distribution. Our model is consistent with a chemokine guided directive component of the collective cell motion, fitting a potential field through a radial kernel basis regression. The implied force field is then given by the gradient of the potential field. Applying our methods to 2-photon data obtained from observations in murine lymph nodes, we compare the motion of recently emigrated vs established B cells within the B cell follicle. Our Bayesian analysis provides us with estimates for the spatial structure of the potential field (see Figure 2), capturing the corresponding force fields in 3 dimensions.
Work in progress
- T. Kepler, I. Manolopoulou, M. West, M. P. Matheu and M. D. Cahalan, 'Analysis of lymphocyte motion by Langevin Processes'.
- Ioanna Manolopoulou, Quanli Wang, Thomas B. Kepler and Mike West. Dynamic Point Processes using Mixture Models for Spatio-Temporal Intensity Functions.
Papers and Presentations
- I. Manolopoulou, M. P. Matheu, M. D. Cahalan, M. West and T. B. Kepler, Bayesian Spatio-Dynamic Modelling in Cell Motility Studies: Learning Nonlinear Taxic Fields Guiding Immune Response. Invited JSM 2012 Journal of the American Statistical Association, Applications and Case Studies discussion paper, to appear.
- I. Manolopoulou, M. Matheu, T. B. Kepler and and M. West, Dynamic spatial modeling in inhomogeneous force fields. Invited talk at ISBA 2010.
- I. Manolopoulou, M. Matheu, T. B. Kepler and and M. West, 'Understanding B cell migration: Inference of chemokine gradients through observation of single cells'. Poster, Frontiers in Mathematical Biology: NSF-NIH PIs Meeting 2010.
