1.08 Brouwer's fixed point theorem

(1.40) Assume, for a contradiction, that \(F(x)\neq x\) for all \(x\in D^2\). Then we can define a map \(G\colon D^2\to\partial D^2\) (where \(\partial D^2\) denotes the boundary circle) as follows: consider the ray starting at \(F(x)\), passing through \(x\) and let \(G(x)\) to be the unique point of intersection of this ray with \(\partial D^2\).

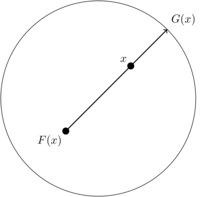
(3.45) If there were a fixed point, we would not know which ray to draw (as \(F(x)=x\)), so this map is only well-defined because we have assumed there are no fixed points.

(3.58) We claim that:

1. \(G\) is continuous; this is intuitively clear, but requires proof (below).
2. \(G(x)=x\) if \(x\in\partial D^2\); this is clear, because if \(x\in\partial D^2\), no matter where \(F(x)\) is, the ray from \(F(x)\) to \(x\) intersects the boundary at \(x\), so \(G(x)=x\).

(5.25) Given these two claims, we get a contradiction as follows. Let \(i\colon\partial D^2\to D^2\) be the inclusion map of the boundary; the composition \(G\circ i\) equals the identity map on \(\partial D^2\) by claim 2. This implies \[id=G_*\circ i_*\colon\pi_1(\partial D^2)\to\pi_1(\partial D^2).\] We have \(\pi_1(\partial D^2)=\mathbf{Z}\), and this is saying that the identity map on the integers factors through the map \(i_*\colon\pi_1(\partial D^2)\to\pi_1(D^2)=0\):

(7.30) This implies that \(G_*\circ i_*=0\). This is impossible, as it implies \(n=G_*(i_*(n))=G_*(0)=0\) for all \(n\in\mathbf{Z}\). Therefore we have a contradiction, and we have proved Brouwer's fixed point theorem, modulo claim 1.

(9.20) It remains to prove claim 1 (that \(G\) is continuous). We can write \(G\) as a composition \(H\circ j\) where:

• \(j\colon D^2\to D^2\times D^2\setminus\{(x,x)\ :\ x\in D^2\}\) is the map \(j(x)=(x,F(x))\).
• (11.30) \(H\colon D^2\times D^2\setminus\{(x,x)\ :\ x\in D^2\}\) is the map defined as follows. Given two distinct points \(x\neq y\) in \(D^2\), let \(H(x,y)\) denote the point where the ray from \(y\) through \(x\) intersects \(\partial D^2\).

(12.25) By definition, we have \(G(x)=H(x,F(x))=H(j(x))\). By the properties of the product topology, the map \(j\) is continuous (more generally, if \(p\) and \(q\) are continuous then \((p,q)\) is continuous). It therefore suffices to show that \(H\) is continuous.

(13.25) We can write \(H\) explicitly in coordinates. The ray from \(y\) through \(x\) is given in parametric form by \(y+t(x-y)\). The condition that the ray meets the boundary of the disc is \[|y+t(x-y)|^2=1,\] which is a quadratic equation in \(t\): \[t^2|x-y|^2+2t(x-y)\cdot y+|y|^2-1=0.\] (Note that the leading term is never zero since \(x\neq y\)). This has solution \[t_\pm=\frac{-2(x-y)\cdot y\pm\sqrt{4((x-y)\cdot y)^2-4|x-y|^2(|y|^2-1)}}{2|x-y|^2}\] We are only interested in solutions with \(t\geq 0\) as the ray only points in one direction. Therefore the point \(H(x,y)\) is \(y+t_+(x-y)\), which is now expressed purely in terms of rational functions and surds, all of which are continuous.