4.02 Homotopy extension property (HEP)

Video

Below the video you will find accompanying notes and some pre-class questions.

Notes

(0.00) In this section, we will introduce the homotopy extension property, a useful tool for proving that different spaces are homotopy equivalent. For example, you can use it to prove that the θ-graph and the figure 8 are homotopic ``just by squishing the middle bar of the θ to a point'' (see image below), or the a sphere with a 1-cell attached (joining the North and South poles) is homotopy equivalent to a pinched torus ``just by squishing the 1-cell to the pinch point''.

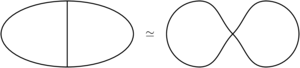
cw-02-01.png

Homotopy extension property

(0.58) Given a space \(X\) and a subspace \(A\), we say that the pair \((X,A)\) has the homotopy extension property (HEP) if, for every continuous map \(F\colon X\to Y\) and every homotopy \(h\colon A\times[0,1]\to Y\) with \(h(x,0)=F(x)\) there exists a homotopy \(H\colon X\times[0,1]\to Y\) such that \(H(x,0)=F(x)\) and \(H|_{A\times[0,1]}=h\).

(2.44) More colloquially, homotopies of functions defined on \(A\) extend to homotopies of functions defined on \(X\) (for given initial data).

(3.29) If \((X,A)\) has the HEP and \(A\) is contractible, then \(X\simeq X/A\), where \(X/A\) denotes the quotient space in which \(A\) is crushed to a single point.

(4.40) To prove that \(X\simeq X/A\), we need to find continuous maps \(q\colon X\to X/A\) and \(g\colon X/A\to X\) such that \(g\circ q\simeq id_X\) and \(q\circ g\simeq id_{X/A}\). The map \(q\colon X\to X/A\) will be the quotient map.

(5.20) Constructing the map \(g\colon X/A\to X\). The subspace \(A\) is contractible, so there exists a point \(a\in A\) and a homotopy \(h_t\colon A\to A\) such that \(h_0=id_A\) and \(h_1(x)=a\) for all \(x\in A\). Since \(A\subset X\), we can think of this as a homotopy \(h_t\colon A\to X\).

(6.14) Using the HEP for the pair \((X,A)\), we get a homotopy \(H_t\colon X\to X\) such that \(H_0=id_X\) and \((H_t)|_{A}=h_t\). At \(t=1\), \(h_1(A)=\{a\}\) and \((H_1)|_A=h_1\), so \(H_1(A)=\{a\}\). Therefore \(H_1=g\circ q\) for some continuous map \(g\colon X/A\to X\) (in other words, \(H_1\) descends to the quotient).

(7.57) The fact that \(g\) is continuous follows from this section on continuous maps out of a quotient space (continuous maps from \(X/\sim\to Y\) are just continuous maps \(X\to Y\) which descend to the quotient). This map \(g\) is going to be our homotopy inverse for \(q\).

(8.20) The map \(g\) is a homotopy inverse for \(q\). We need to prove:

  1. (9.00) \(g\circ q\simeq id_X\): This holds because \(g\circ q=H_1\simeq H_0=id_X\).

  2. (9.22) \(q\circ g\simeq id_{X/A}\): Since \((H_t)|_{A}=h_t\), the homotopy \(q\circ H_t\colon X\to X/A\) has the property that \((q\circ H_t)(A)\subset q(h_t(A))\subset q(A)\). Since \(q(A)\) is a single point, this implies that \(q\circ H_t\) factors as \(\bar{H}_t\circ q\) for some continuous map \(\bar{H}_t\colon X/A\to X/A\) (again, using our results on continuous maps out of a quotient space).

    (11.22) We have \(\bar{H}_0=id_{X/A}\) since \(H_0=id_X\). We want to show that \(\bar{H}_1=q\circ g\). We first notice that \[\bar{H}_1\circ q=q\circ H_1=q\circ (g\circ q)=(q\circ g)\circ q,\] which implies \(\bar{H}_1=q\circ g\) if we can cancel the extra \(q\)s on each side of the equation.

    (12.34) We can cancel the \(q\)s because \(q\) is surjective (it's a quotient map) and surjective maps have right-inverses (so can be cancelled from the right).

(14.05) We will see in the next video that if \(X\) is a CW complex and \(A\) is a closed subcomplex then \((X,A)\) has the HEP.

Pre-class questions

  1. Assuming that you can use the HEP with impunity, which of the following spaces are homotopy equivalent to one another?

cw-02-02.png

Navigation

CC-BY-SA, Jonny Evans 2017