Research Interests

Differential geometry

Partial differential equations with boundary conditions

Mean curvature flow and related geometric flows

Geometric analysis

Calculus of variations

Preprints

(12) C. Evans, B. Lambert and A. Wood, Lagrangian mean curvature flow with boundary conditions. Preprint.

(11) D. Ballesteros-Chavez, W. Klingenberg and B. Lambert, Prescribed k-symmetric curvature hypersurfaces in de Sitter space. Preprint.

Peer Reviewed Papers

(10) B. Lambert and J. Scheuer Isoperimetric problems for spacelike domains in generalized Robertson-Walker spaces. To appear in the Journal of Evolution Equations. Preprint.

(9) B. Lambert, J. D. Lotay and F. Schulze, Ancient solutions to Lagrangian mean curvature flow. To appear in Annali della Scuola Normale Superiore di Pisa, Classe di Scienze. Preprint.

(8) B. Lambert and J. D. Lotay, Spacelike mean curvature flow. To appear in The Journal of Geometric Analysis. Preprint.

(7) B. Lambert, A remark on gradient estimates for spacelike mean curvature flow with boundary conditions. Proceedings of the Edinburgh Mathematical Society, Volume 62 (2019), Issue 2, pages 459--469. Preprint.

(6) B. Lambert and J. Scheuer, A geometric inequality for convex free boundary hypersurfaces in the unit ball, Proceedings of the American Mathematical Society, Volume 145 (2017), Issue 9, pages 4009 -- 4020. Preprint.

(5) B. Lambert, Construction of maximal hypersurfaces with boundary conditions, Manuscripta Mathematica, Volume 153 (2017), pages 431 -- 454. Preprint.

(4) B. Lambert and J. Scheuer, The inverse mean curvature flow perpendicular to the sphere, Mathematische Annalen, Volume 364 (2016), Issue 3, pages 1069 -- 1093. Preprint.

(3) B. Lambert, The constant angle problem for mean curvature flow inside rotational tori, Mathematical Research Letters, Volume 21 (2014), Issue 3, pages 537--551. Preprint.

(2) B. Lambert, The perpendicular Neumann problem for mean curvature flow with a timelike cone boundary condition, Transactions of the American Mathematical Society, Volume 366 (2014), pages 3373--3388. Preprint.

(1) B. Lambert, A note on the oblique derivative problem for graphical mean curvature flow in Minkowski space, Abhandlungen aus dem Mathematischen Seminar der Universit\"at Hamburg, Volume 82, Issue 1 (2012), pages 115--120. Link.

A few pictures

Unwinding a jester's hat

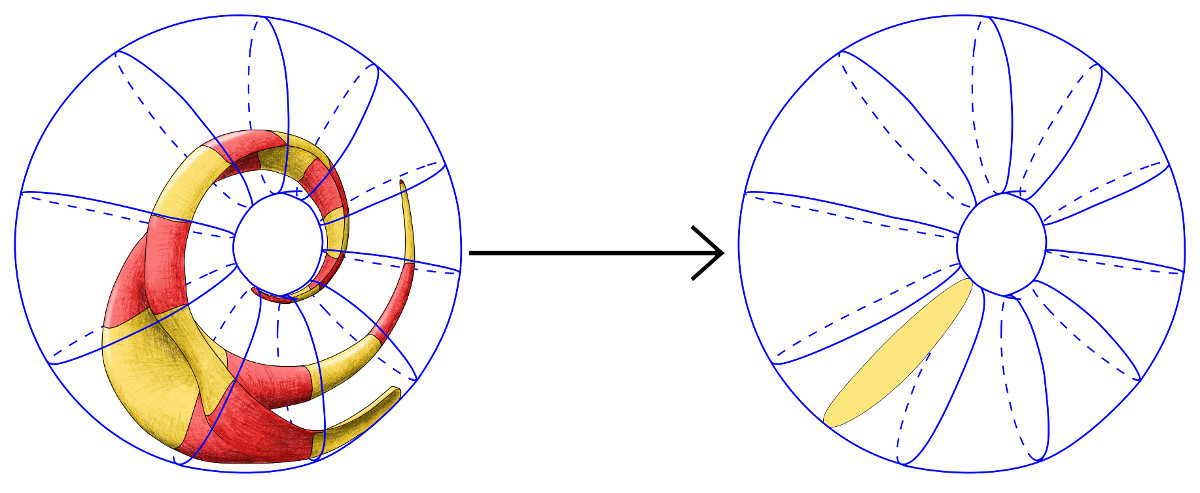
An initial "jester's hat" hypersurface inside a rotational torus flows by mean curvature flow with a Neumann boundary condition to a flat cross-section of the torus. The results of (3) indicate that all embedded initial hypersurfaces transversal to the rotational vector field inside the torus flow for all time and converge to a flat cross-section.

Equivariant examples of Lagrangian mean curvature flow

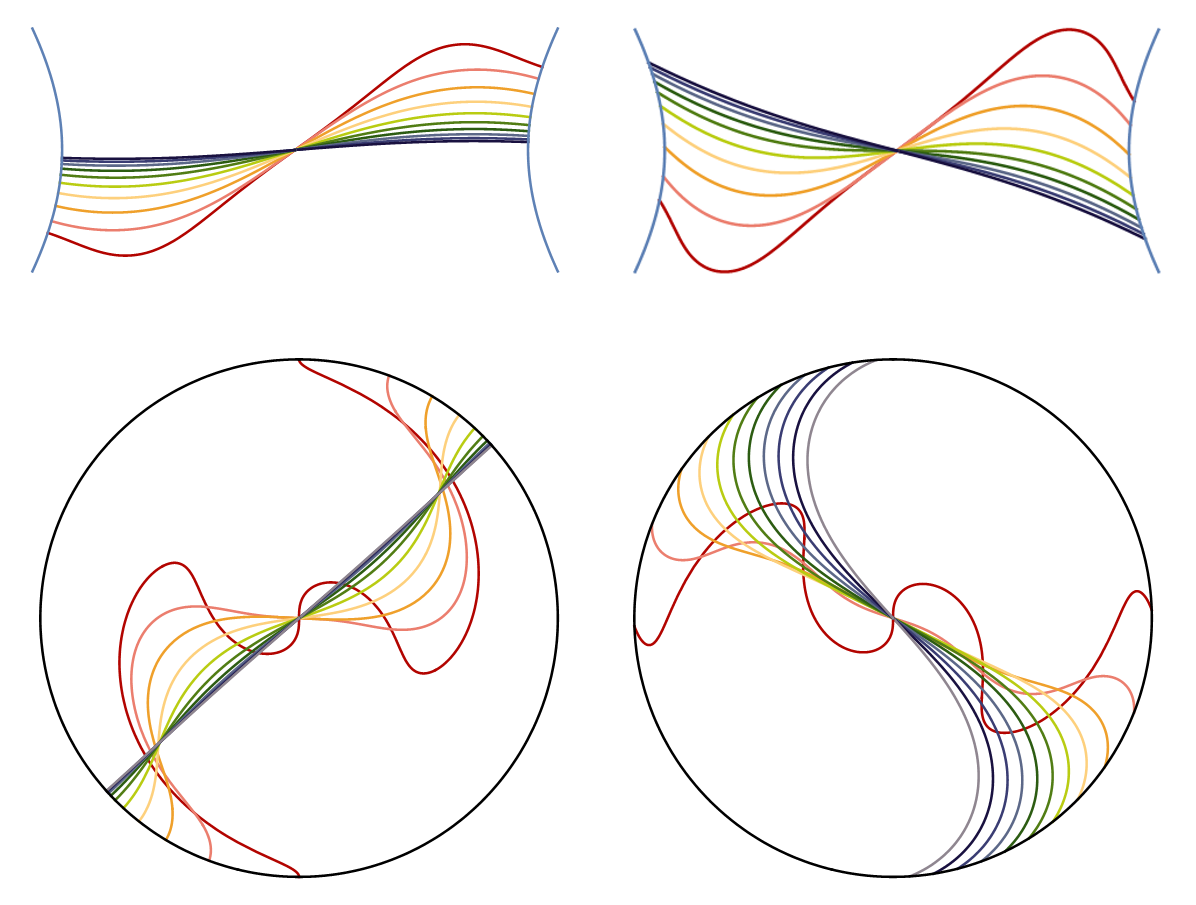
These pictures show the behaviour of Lagrangian mean curvature flow with boundary conditions (LMCF+BC), and they are courtesy of my collaborator Albert Wood. Each line represents a moving two dimensional surface in four dimensional space, where the first surface is in red and then the subsequent surfaces move through the colours of the rainbow.

The first row are flows with boundary on the Lawlor neck, and here we see the flow converging as time goes to infinty (or equivalently, as the colour becomes dark blue) to a straight line which represents a special Lagrangian.

The second row shows rescaled LMCF+BC inside a Clifford torus which is also flowing by Lagrangian mean curvature flow. The Clifford torus is a self shrinker under (non rescaled) LMCF (it may be thought of as the Lagrangian equivalent of the shrinking sphere for mean curvature flow) and in this rescaled version time going to infinity (that is, the surfaces becoming dark blue) corresponds to the singular time of the flowing Clifford torus. The first of these (for a perpendicular boundary condition) shows convergence to a special Lagrangian.

We have proven that the behaviour in the previous two points holds true in generality for almost calibrated starting data for LMCF+BC. However, in the final picture our flow has a non perpendicular boundary condition on the Clifford torus, and instead here the rescaled LMCF+BC appears to converge to a rotating solution to the rescaled flow! Numerical tests appear to indicate that this behaviour generally holds. Note that the rotating solution is equivalent to a rotating shrinking solution to unrescaled LMCF+BC.

Stable, unstable and one-sided stable maximal surfaces

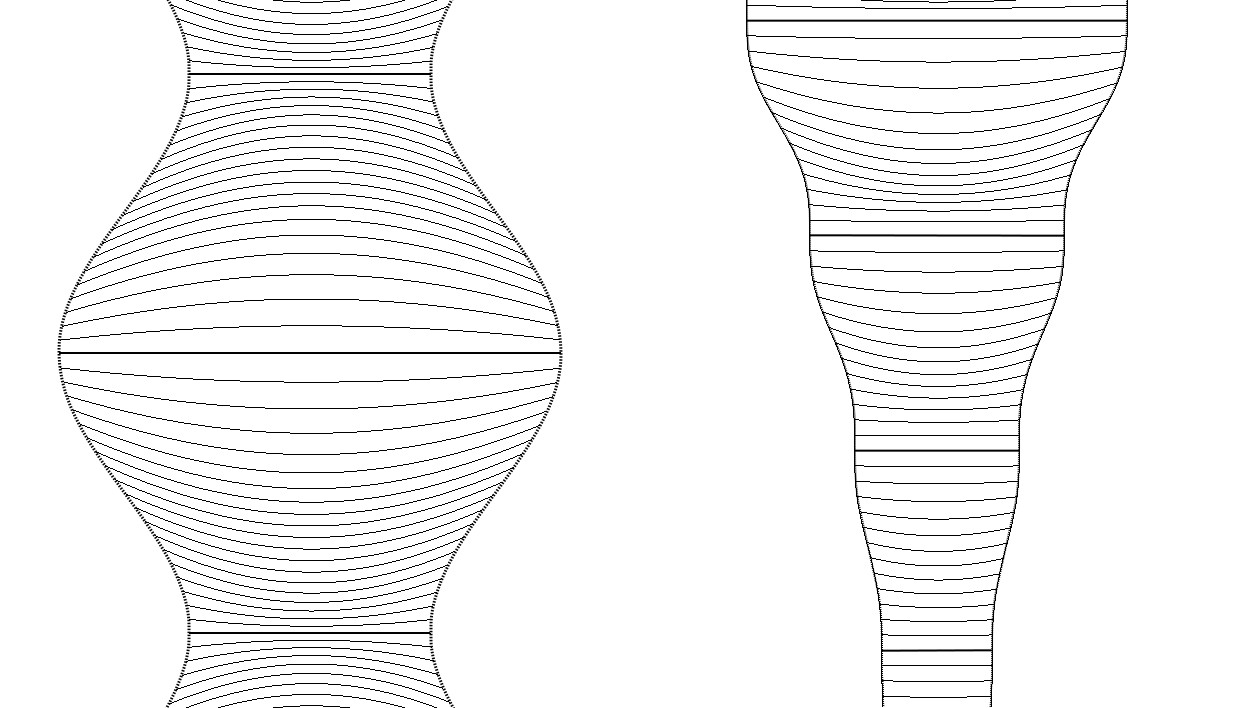
Here we see the cross-section of rotationally symmetric spacelike constant mean curvature foliations perpendicular Lorenzian boundary manifolds in Minkowski space, where the straight horizontal lines represent flat maximal surfaces. As the constant mean curvature foliations may be used to construct comparison solutions for spacelike mean curvature flow with boundary conditions, we see three different behaviours:

The maximal surface where all the lines of the foliation bend towards the maximal surface (such as the horizontal line at the fattest point of the sine wave on the left) are stable under the flow (i.e. mean curvature flow that starts near to the maximal surface flows back to the surface).

The maximal surface at the thinnest part of the sine wave is unstable.

Meanwhile on the left we see a sequence of maximal surfaces which are one sided stable (i.e. if perturb the maximal surface only in the downwards direction, it will be pushed back to the initial maximal surface, but if we perturb only in the upwards direction, the surface flows to the next maximal surface up). Full details of these results may be found in (5) above.

Death's Trumpet

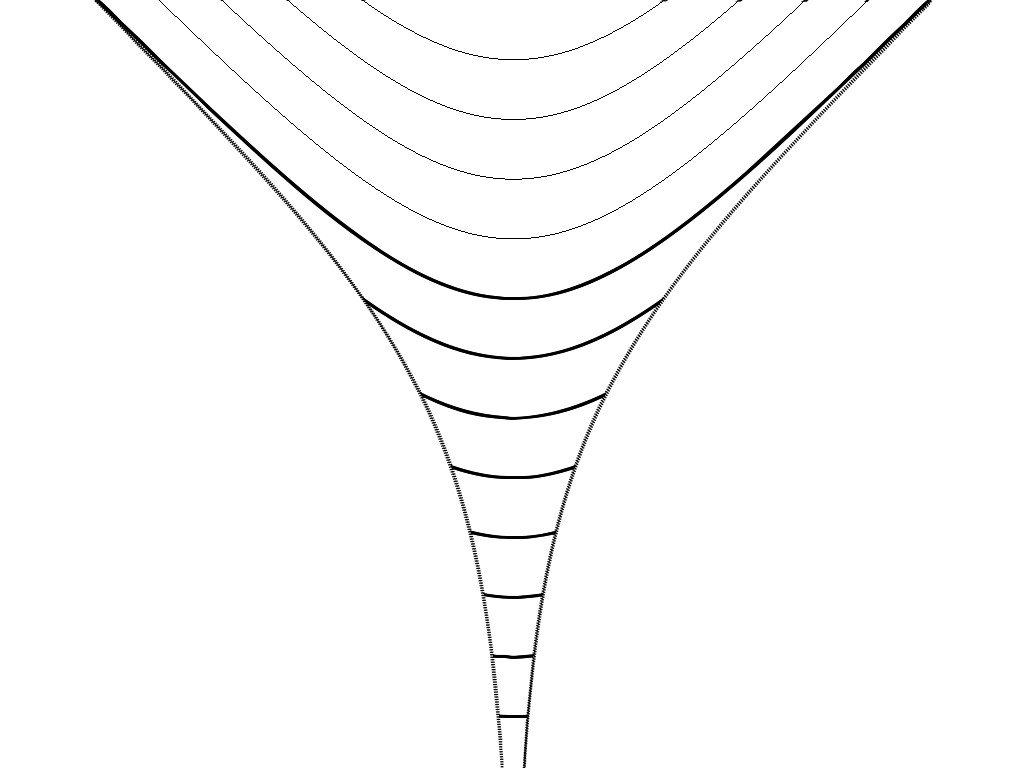
Grim reaper solution coming out of a trumpet

Here is an interesting example of singular behaviour of mean curvature with a Neumann boundary condition in Minkowski space: We see here the grim reaper solution to spacelike mean curvature flow in 2 dimensional spacelike mean curvature flow given by log(cosh(x+t)), starting from negative t. The boundary manifold or "trumpet" is given by log(|sinh(x)|), and the grim reaper solution is (Minkowski) perpendicular to the trumpet at any point it intersects it. We therefore have a solution to mean curvature flow with a Neumann boundary condition whose maximum curvature explodes as t tends towards 0. Additionally the flow becomes "lightlike at infinity" at time t=0. This implies that some curvature conditions are required on boundary manifolds if we wish to get bounded geometry in the form of gradient and curvature estimates of a flowing hypersurface. Wierdly, although the Neumann boundary condition no longer makes sense for t>0, there is no problem for the flow to continue on the interior (the thinner lines in the picture). While this is an interesting example, I admit that I include it here partly in the hope the name "Death's Trumpet" catches on. For more results on gradient estimates for spacelike mean curvature flow see (5) above.

Convex inverse mean curvature flow inside ellipsoids

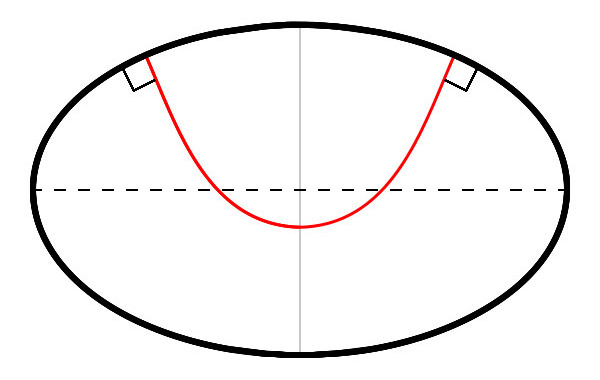
In (4) we see that for convex initial data, IMCF perpendicular to the unit sphere exists for a finite time before converging to a flat minimal hypersurface intersecting the unit sphere on an equator. The flow therefore becomes globally singular, with the speed of the flow becoming infinite everywhere at the final time. The above is an example that demonstrates if we flatten our sphere even slightly this result is no longer true. The above shows convex rotationally symmetric initial data intersecting the unique rotationally symmetric topological disc which is minimal. Since the flow cannot change direction the results of (4) cannot hold. In fact due to a minimum speed bound, the above must form a (nonglobal) singularity in finite time.

Ben Lambert