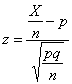Binomial test
This HTML document allows you to test whether a score in a forced choice task is significantly different from chance. This is done by a binomial test. Note: by using the formula below, you can compute whether your score is different from any other specified score. Your browser must be JavaScript enabled to deal with this form. Mozilla, Netscape, Safari, and Internet Explorer should do.

The assumptions for the test are that a) the data are dichotomous, b) observations should be independent from each other, and c) the total number of observations in category A multiplied by the total number of observations (i.e. A + B) > 10, and  that the total number of observations in category B multiplied by the total number of observations > 10 (this way we can use the normal approximation for the binomial test and calculate the z-score).

What is actually done here is that the proportion of the observed score (X) is computed, which is then converted to a z-score given the probability of chance (p) and its reciprocal (q) (which are used to compute the standard deviation of the distribution) and the total number of observations (n). The probability of the z-score can be looked up from Z table (see below for some critical values).  One equation is:

(from A. Clarke's page here)

Usage: Fill in three fields: Score (i.e., the actual score obtained by the participants), Chance level (e.g., 50% correct; remember to calculate a raw score!), and Total number of observations (i.e., total number of items in your test), then press the "Calculate" button to compute the z-score.

Interpretation:
If z <   1.64 --> the observed score is not significantly different from chance level
If z >= 1.64 --> the observed score is significantly different from chance at level p < .05 (one-tailed)
If z >= 1.96 --> the observed score is significantly different from chance at level p < .025 (one-tailed)
If z >= 2.33 --> the observed score is significantly different from chance at level p < .01 (one-tailed)
If z >= 2.57 --> the observed score is significantly different from chance at level p < .005 (one-tailed)


Score:       
Chance:    
# of items: 
Z-score:     

There are several other (and more convenient) Web resources to run a binomial test. One with additional information on Binomial test is on the Web site maintained by Simple Interactive Statistical Analysis (SISA) at: http://home.clara.net/sisa/binomial.htm.
A simple explanation of binomial test is provided by Aaron Clarke (University of York).

Send comments etc. to: jyrtuoma@utu.fi